gabimo
Mechanical
- May 2, 2013
- 124
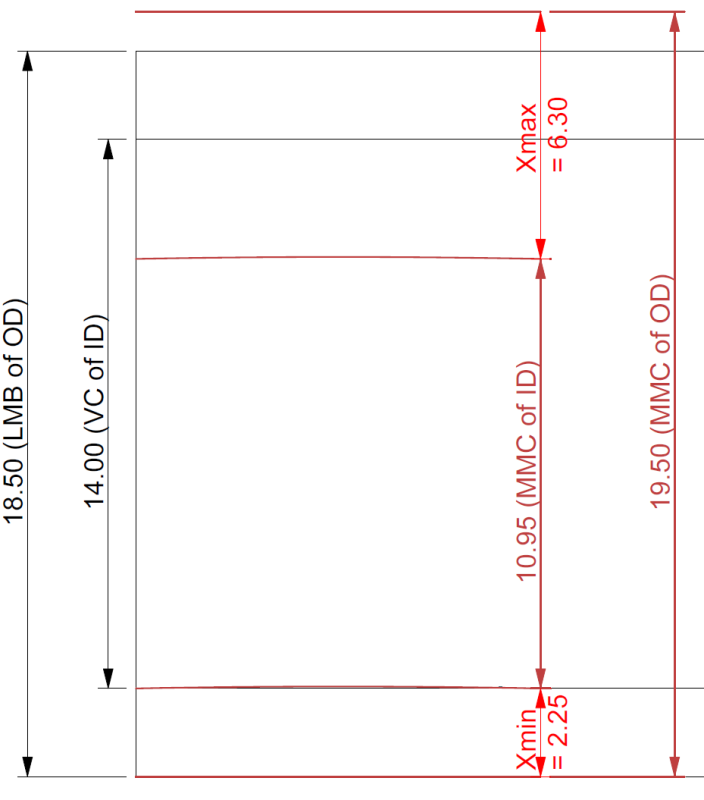
An “adjusted” (positional tolerance-wise Ø3mm instead of 0 at LMC) picture from ASME standard. (7-17/2009)
Question: What would be X min. and X MAX. for the case shown?
Question: What would be X min. and X MAX. for the case shown?