psychedomination
Structural
Hi there,
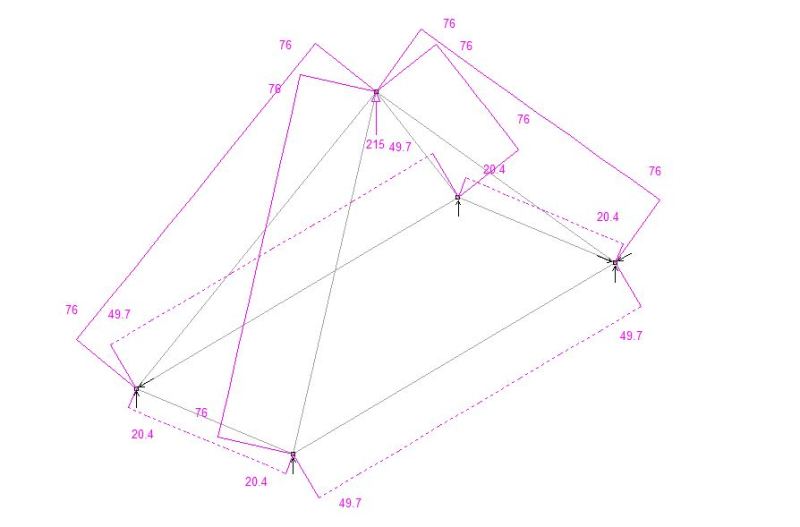
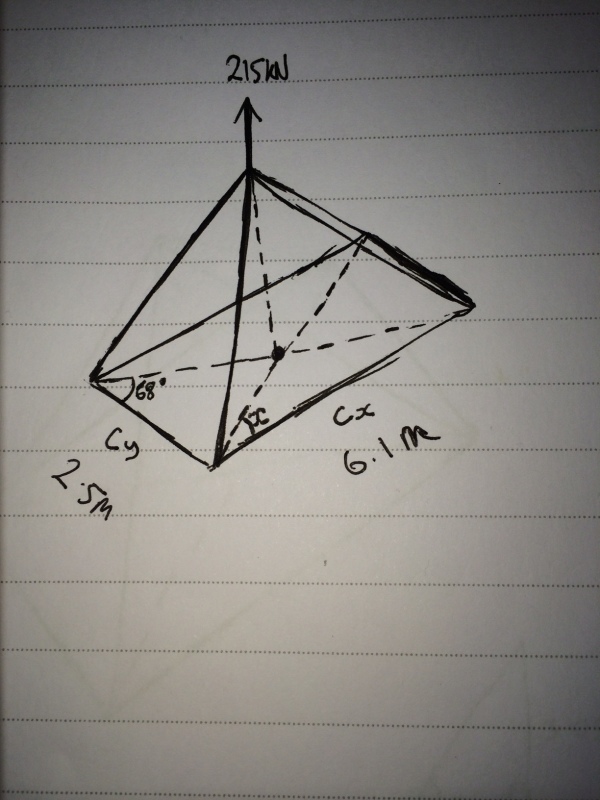
I need some help accurately calculating the compression forces in the members Cy and Cx shown in the attached image. I know how to calculate the compression in 2D triangles but not sure what to do when the object becomes 3D (includes the z axis). If it helps the cables attached to the frame are inclined at 45 degree angles to the vertex (z axis).
I calculated an estimate of the compression forces to use in my design, however I am looking to learn a more accurate calculation methodology for this current project along with all future projects.
Any help will be appreciated.

- Psyche
I need some help accurately calculating the compression forces in the members Cy and Cx shown in the attached image. I know how to calculate the compression in 2D triangles but not sure what to do when the object becomes 3D (includes the z axis). If it helps the cables attached to the frame are inclined at 45 degree angles to the vertex (z axis).
I calculated an estimate of the compression forces to use in my design, however I am looking to learn a more accurate calculation methodology for this current project along with all future projects.
Any help will be appreciated.

- Psyche