Regarding the design of spacecraft structures, what is meant by "static" and "dynamic" acceleration?
Any help is much appreciated!
Launch vehicle providers always include a table of Spacecraft Design Limit Load Factors in their user guides to use for spacecraft preliminary design.
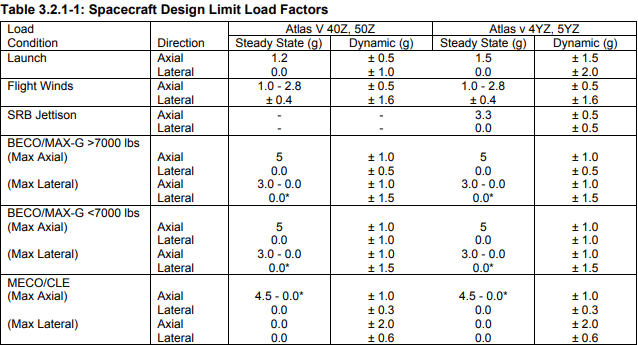
For example, the below table is taken from the ULA Atlas V User Guide:
Another example is from Wijker's book Spacecraft Structures:
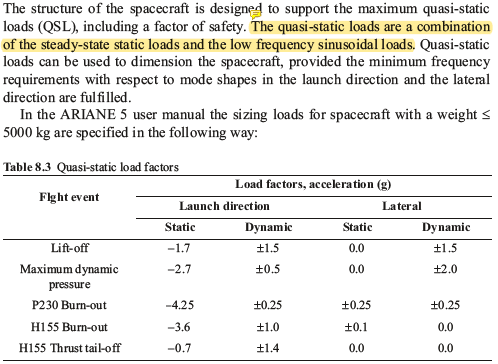
I've highlighted what seems to be the author's description of the two components.
From another document (ECSS-E-HB-32-26A: Spacecraft Loads Analysis Handbook), they define "steady-state acceleration" as the same as static acceleration (constant magnitude and direction) and can be thought of as the average acceleration through the center of gravity.
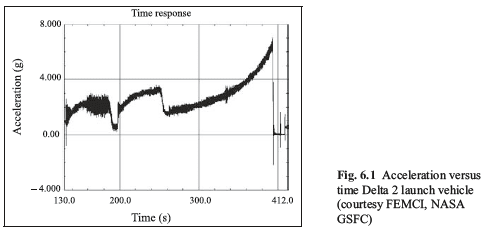
I interpret this as if you were to remove all the vibration from the following figure, resulting in a smooth line. Is this correct? If so, it seems weird to consider steady-state acceleration the same as static. Static to me means constant with time, which obviously it is not. I guess this is why the term "quasi-static" is sometimes used instead? Static acceleration is a very confusing term to me.
Is dynamic acceleration then the acceleration due to the low-frequency sinusoidal loads such as POGO or random vibration due to acoustic noise from engines firing? This would be the noise in the below image.
Second part of the question is how are the loads actually used? I understand they are applied to the fixed spacecraft's CG, but do I add them together?
For example, using Table 3.2.1-1 from Atlas V, to cover the worst-case, I would run these two cases?
[ol 1]
[li]Max axial[/li]
This occurs during BECO and I would apply 6 g's axially (steady-state + dynamic) and 1.5 g laterally together at the same time
[li]Max lateral[/li]
This occurs during launch and I would apply 3.0 g's axially and 2 g's laterally together at the same time
[/ol]
Any help is much appreciated!
Launch vehicle providers always include a table of Spacecraft Design Limit Load Factors in their user guides to use for spacecraft preliminary design.
For example, the below table is taken from the ULA Atlas V User Guide:

Another example is from Wijker's book Spacecraft Structures:

I've highlighted what seems to be the author's description of the two components.
From another document (ECSS-E-HB-32-26A: Spacecraft Loads Analysis Handbook), they define "steady-state acceleration" as the same as static acceleration (constant magnitude and direction) and can be thought of as the average acceleration through the center of gravity.
I interpret this as if you were to remove all the vibration from the following figure, resulting in a smooth line. Is this correct? If so, it seems weird to consider steady-state acceleration the same as static. Static to me means constant with time, which obviously it is not. I guess this is why the term "quasi-static" is sometimes used instead? Static acceleration is a very confusing term to me.
Is dynamic acceleration then the acceleration due to the low-frequency sinusoidal loads such as POGO or random vibration due to acoustic noise from engines firing? This would be the noise in the below image.

Second part of the question is how are the loads actually used? I understand they are applied to the fixed spacecraft's CG, but do I add them together?
For example, using Table 3.2.1-1 from Atlas V, to cover the worst-case, I would run these two cases?
[ol 1]
[li]Max axial[/li]
This occurs during BECO and I would apply 6 g's axially (steady-state + dynamic) and 1.5 g laterally together at the same time
[li]Max lateral[/li]
This occurs during launch and I would apply 3.0 g's axially and 2 g's laterally together at the same time
[/ol]
