SpaceEngineer4
Aerospace
- Aug 8, 2023
- 12
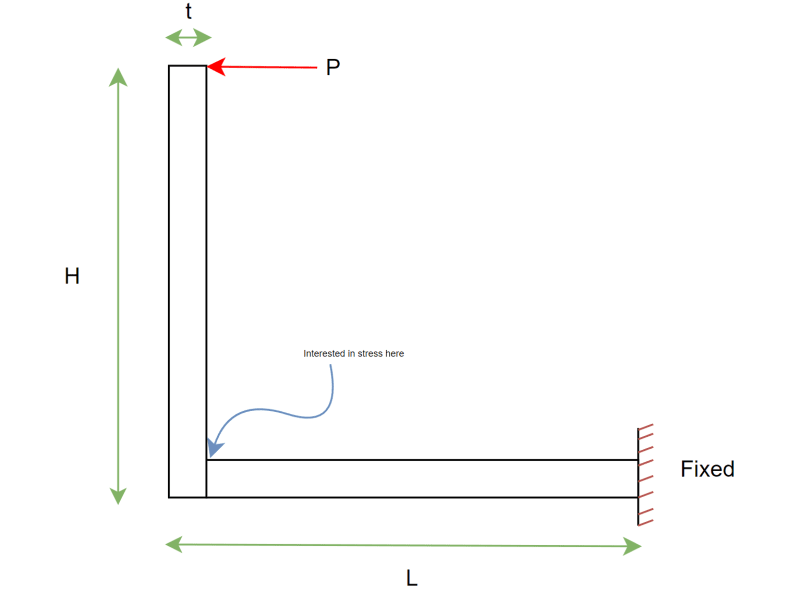
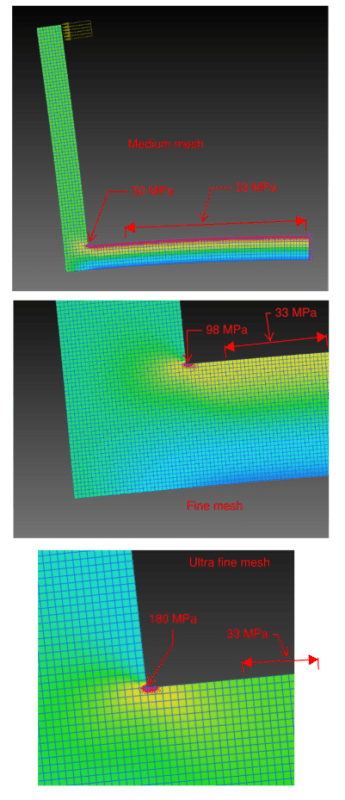
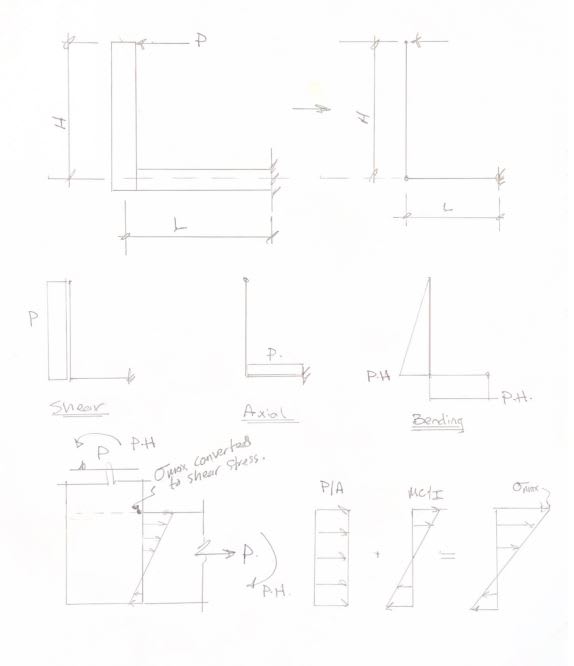
Salutations everyone. I've got a question regarding the stress in a frame, or one could call it a beam bent 90 degrees. Assuming the beam has the dimensions shown in the image, I'm having trouble doing hand calculations at the corner indicated in the photo. Obviously there are the classical bending moment contributions, Mc/I with stress concentrations. However, when I run the FEA on this continuous beam, I notice that there is a significant shear stress on the corner indicated in the photo. I did not expect this because according to beam theory, the shear stress on the outer fibers of a section should be zero. However, the shear stress may be very big in that corner. Could anyone help out with some guidance on how one might go about calculating stresses in a continuous beam/frame such as this? My dearest thanks to you all.
Cheers.
~Robert