The physics of Bungee Jumping 1

[GregLocock]

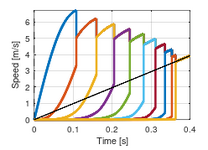
Never seen the attraction myself, but this paper investigates why a bungee jumper accelerates at more than 1g

https://www.fc.up.pt/pessoas/psimeao/desafios/Bungee_Jumper_maior_que_g.pdf

Good stuff.

 

[LionelHutz]

Like, "Push with a rope"?

So, the bungie cord is pushing upwards on the jumper?

 

[waross]

So, the bungie cord is pushing upwards on the jumper?

How can a falling cord exert a force on a body to accelerate the body at grater than 1 g unless the falling cord is falling at more than one g?
Ar we considering stretch in the cord or has that been discarded.
Sky Diving and Bungee Jumping.
Neither one is my idea of a stroll in the park.
Is there a psychological connection between stepping out of a perfectly good airplane and stepping off a perfectly good bridge?
No disrespect to Sky Divers and Bungee Jumpers.
You can tell me all about in the safety of a coffee shop. grin.

 

[XR250]

Another factor.
Thanks Mint.
Would that add to the acceleration?

(I will have to put old boring reruns on TV tonight and bore myself to sleep.
Else I will be awake all night trying to figure this out.

Nite all.

The OP's article ignores any stretch in the bungee cord in their analysis. So it should be the same for a rope.

 

[btrueblood]

Mint, thanks. The diagrams (esp. second set) are explaining what I'm talking about.

Prex, You've never seen a metal cable snap? Substantially inextensible, but there is a lot of energy stored in the elastic strain energy when it's taut. Same with long chains. Smart people working in the logging industry know to never stand inline to either (the dumber ones are dead now). The strain of a steel chain may dissipate quicker than a bungee, but it will still act on the jumper. You can't say the strain energy in a suspended flexible element (bungee, cable, chain) is non-zero. Nor can you say the suspended cable is massless. So, the suspended bungee/cable/chain contracts when the restraint is removed (jumper steps off the platform). At that instant, as Mint is showing in his diagrams, there is a tensile force acting between the center of mass of the suspended loop of flexible element and the center of mass of the jumper's body, creating a net downward acceleration in addition to gravity. The argument of internal friction dissipating the strain energy is not wrong, certainly some of it will, but why does a severed cable or chain whip and injure people - why didn't "internal friction" keep it from doing that?

Yes, the strain energy in the bungee loop below the jumper diminishes to zero during the fall, and the loop still attached to the bridge begins to gain strain energy as more weight of the bungee becomes suspended by it. And the mass of bungee in the loop below the jumper diminishes as well. At the instant the loop disappears, the bungee is just gone taut, the strain energy and tensile force on the jumper is zero. But it was non-zero until then.

XR250, another structural? Who cares about the OP's article - it doesn't in my mind solve the question of where the extra acceleration comes from, the main point of the article is that they MEASURED an acceleration greater than could be explained by gravity. You could argue that the experiment is wrong somehow, but you fail to explain why.
" So it should be the same for a rope." Why? Rope is a flexible and non-zero mass also, why would the extra acceleration not occur with a rope?

 

[Compositepro]

Here is an interesting and relevant video of a stretched Slinky being dropped. Just something to consider.

 

[GregLocock]

Astonishing. I see how and why, but that gets my vote for the most unintuitive result I've seen this year. Late edit - if you did this with a conventional coil spring it would just fall on the floor. It's got something to do with k and m, obviously.

Oh, and here's some boring old differential equations for the bungee jump calculation

https://iopscience.iop.org/article/10.1088/0031-9120/45/1/007/pdf which can be summarised as



grabbed from https://allendowney.blogspot.com/2018/07/the-physics-of-bungee-jumping.html

 

[MintJulep]

stretched Slinky being dropped.

I can't make the equations for that in my mind yet.

Maybe if I try to write the i down later...

 

[MintJulep]

 

[GregLocock]

Best me and ChatGPT can come up with for a falling slinky. As you can see it is not right, the bottom of the spring is rising gently initially, and the minimum length is not the compressed length (.057m)

 

[prex]

Sorry guys, I need to make amends.
I now see where is the point: Newton's law only holds, for an isolated system, if the mass in F=ma is constant.
This problem has something in common with the well known phenomenon of ice skaters, when they spin on the spot at varying speeds by narrowing or widening their arms and body. In that case the mass is constant, but the moment of inertia changes, and a rotational acceleration is imparted on the spinning body without the intervention of external forces.
In the bungee problem, the key factor is that part of the cord or rope goes progressively at rest, but its energy is not completely lost, it is in fact (partly) transferred to the moving body, and an acceleration greater than g can be seen by the falling body because the mass in the system is not constant.
So sorry again btrue and Greg, though you were not that clear in explaining the foundation of this surprising result . And btrue, one last comment: I've seen metal cable snaps, but that one is a different phenomenon: it is due to the elastic strain energy that was stored in the cable before the snap. What is similar to the bungee problem is the ultrasonic crack of a whip: the whip, that is substantially inextensible, goes progressively at rest, and all the initial energy imparted is transferred to the tip.

 

[MintJulep]

More on the slinky – Ted Bunn’s Blog

Interesting and enlightening.

 

[GregLocock]

Luckily someone in matlab world produced this lovely graph for a dropped slinky. André de Souza Mendes (2025). Slinky drop (https://github.com/andresmendes/Slinky-drop/releases/tag/1.0.1), GitHub. Retrieved February 1, 2025. For an animation

For my plots I changed the parameters a bit so it isn't the same as the video. So, initially each mass is in equilibrium. When the top one is released it is being pulled down by the tension needed to support the rest of the masses, plus g. The bottom one is still in equilibrium so doesn't move. As you can see from the velocity plot, the initial acceleration of m1 is 4 m/s in 0.04s, ie 10g, as expected. Damn this is neat. Having said that the velocity plot is a bit misleading, even if it is pretty. This makes it clear

 

[GregLocock]

prex- the situation is indeed akin to a whip, even the tip of an inextensible cable drops faster if doubled and held at one end than if you drop the whole thing.

 

[Compositepro]

Another one for your viewing pleasure. This one illustrates how torque on each angled wrung as it strikes a table top causes an increase in force pulling down on the wrungs above that are still falling. This is probably what causes the tip of a whip to accelerate so much.

 

[XR250]

Maybe there is some analogy to this....

 

[LionelHutz]

How can a falling cord exert a force on a body to accelerate the body at grater than 1 g unless the falling cord is falling at more than one g?

There's already lots of info and theory being posted. "Can't push with a rope" isn't much of a rebuttal for disputing the test results.

 

[GregLocock]

XR250's experiment isn't much help, in my opinion. The falling ladder one is weirder than the other two, slinky, and bungee. Slinky is the easiest to understand, in retrospect.