eng-wannabe
Mechanical
The question in a nutshell: A torque is applied to Link A, what is the resultant torque to Link B?
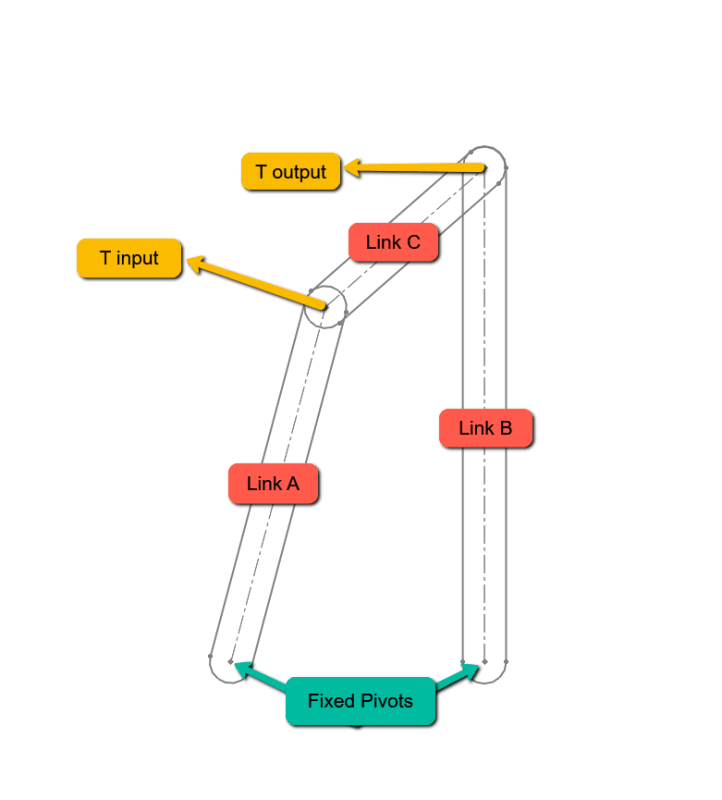
Here is a simplified diagram:
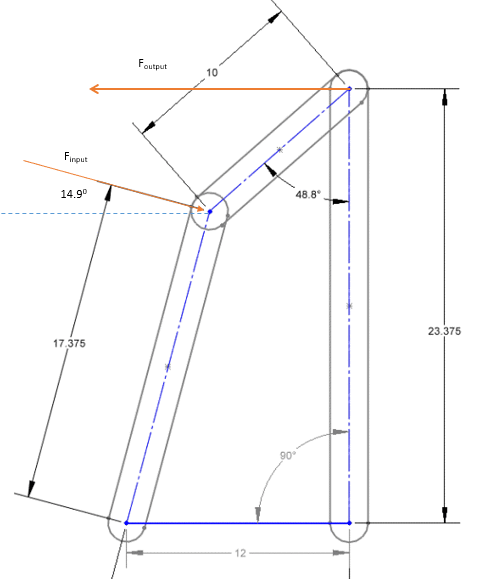
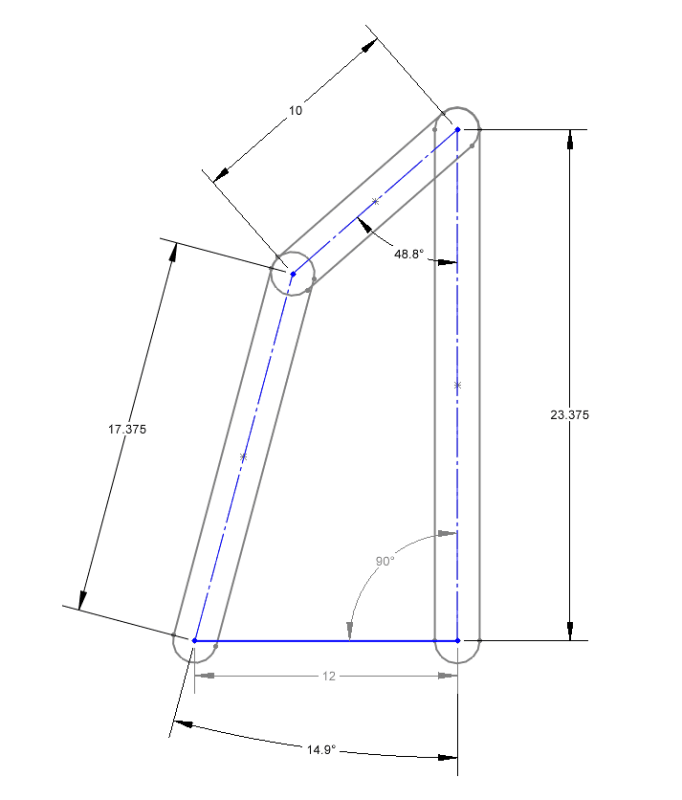
Here is the geometry:
Basically, I have a system wherein a link arm (Link A) is attached to a gearbox, that link arm is attached to a short link (Link C) that is then attached to a third link (Link B), or the object that I am seeking to rotate. For a given input torque (to Link A) I would like to calculate the resultant torque to Link B in various positions, the position being shown is the starting position, Link B will be rotated CCW in 10° increments until it rests in the 9:00 position.
I have contextualized the torque as perpendicular vectors that converge in space, the geometry of which is used to create an output percentage. The torque geo being:
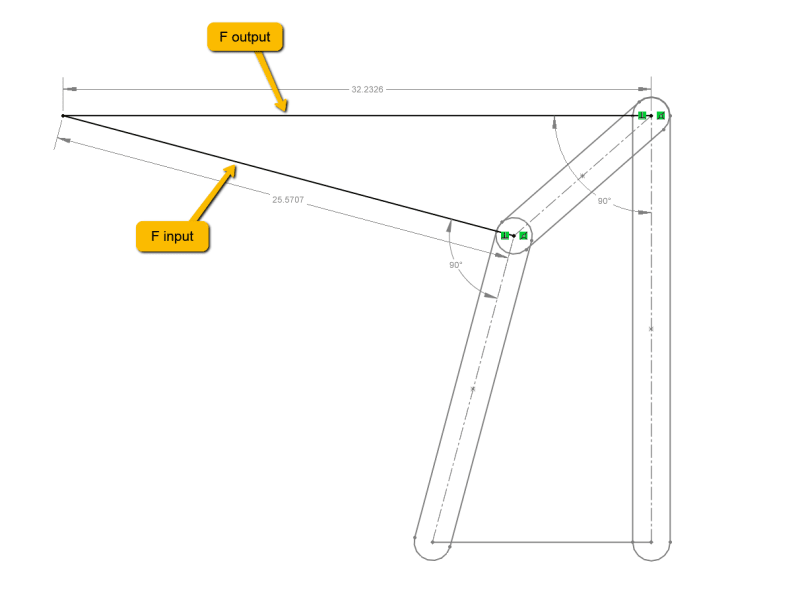
The output percentage being: 1.26 or 126%
My question to the group is: does this track? Is there a better way to calculate this?
Here is a simplified diagram:

Here is the geometry:

Basically, I have a system wherein a link arm (Link A) is attached to a gearbox, that link arm is attached to a short link (Link C) that is then attached to a third link (Link B), or the object that I am seeking to rotate. For a given input torque (to Link A) I would like to calculate the resultant torque to Link B in various positions, the position being shown is the starting position, Link B will be rotated CCW in 10° increments until it rests in the 9:00 position.
I have contextualized the torque as perpendicular vectors that converge in space, the geometry of which is used to create an output percentage. The torque geo being:

The output percentage being: 1.26 or 126%
My question to the group is: does this track? Is there a better way to calculate this?