aniiben
Mechanical
- May 9, 2017
- 158
3DDave said:Q1 - referring to a datum feature in a way that it was not initially constrained is a potential problem for understanding the condition. See previous discussion where I make clear that Figure 4-16 (c) is clearly evaluated incorrectly in the standard.
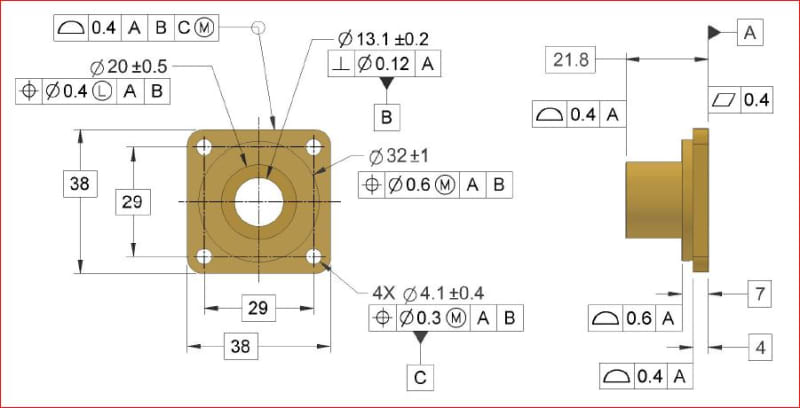
Inspired by a statement made in a previous discussion and also by some of my misunderstandings of the standard’s intent on dealing with datum features of size called at RMB and also at MMB, I would like to ask the members of this forum how would you consider the datum reference frame shown in the embedded picture.
Case 1: A│B│C(M)│
----Datum feature B at RMB (shown in the picture) ---
Is this datum structure or DRF valid? If yes, are there any issues with the violation of datum feature precedence order?
Case 2: A│B(M)│C(M)│
----Datum feature B at MMB (NOT shown in the picture) ---
Same open ended questions as for case#1.