Hi all,
I have a number of sites where the pipework was sized to cater for a flow on the day. Thanks to growing populations, the station needs to be upgraded.
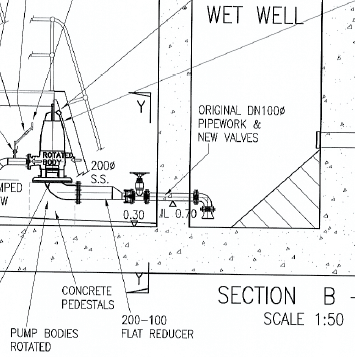
It's easy to increase pump and pipe sizes "in-station" to cater for the increased flows. However what is often ignored is the pipework through the wetwell/drywell wall. and by association the bellmouth in the wetwell.
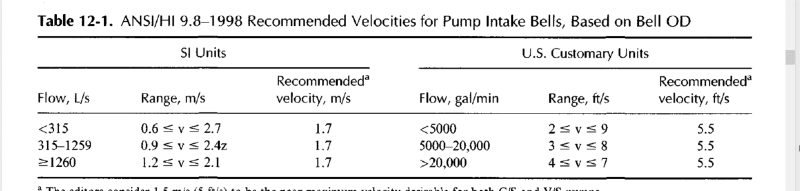
There are industry standards stating the clearance between the underside of the bell mouth and the wetwell floor. Typically D/2 to D/4.
Invariably what happens is the "100mm" pipe through the wall had a bell mouth with a clearance of (Bellmouth OD - 185mm/2 = 92.5mm underside clearance).
The station is upgraded to a 150mm (pipe through the wall) in station. So the bellmouth should have a clearance of (Bellmouth OD of 245mm/2 = 122.5mm).
But the pipe through the wall and bell mouth were not upgraded, so we have a 100mm pipe/bellmouth with a 150mm velocity.
The question is, does anyone have the formula for the calculate the annular velocity entering the bellmouth.
Thanking you all in anticipation.
Nutzman
I have a number of sites where the pipework was sized to cater for a flow on the day. Thanks to growing populations, the station needs to be upgraded.
It's easy to increase pump and pipe sizes "in-station" to cater for the increased flows. However what is often ignored is the pipework through the wetwell/drywell wall. and by association the bellmouth in the wetwell.
There are industry standards stating the clearance between the underside of the bell mouth and the wetwell floor. Typically D/2 to D/4.
Invariably what happens is the "100mm" pipe through the wall had a bell mouth with a clearance of (Bellmouth OD - 185mm/2 = 92.5mm underside clearance).
The station is upgraded to a 150mm (pipe through the wall) in station. So the bellmouth should have a clearance of (Bellmouth OD of 245mm/2 = 122.5mm).
But the pipe through the wall and bell mouth were not upgraded, so we have a 100mm pipe/bellmouth with a 150mm velocity.
The question is, does anyone have the formula for the calculate the annular velocity entering the bellmouth.
Thanking you all in anticipation.
Nutzman