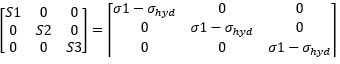-
1
- #1
MCA1983
Aerospace
- Sep 30, 2023
- 17
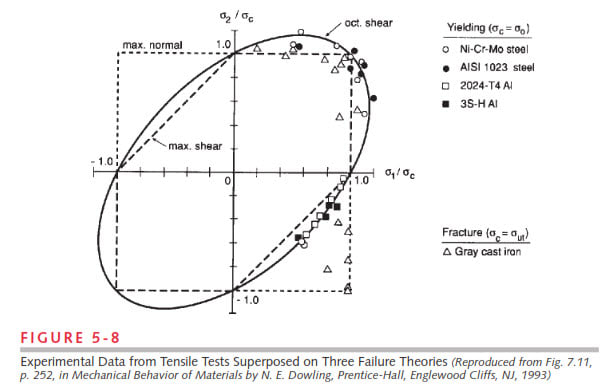
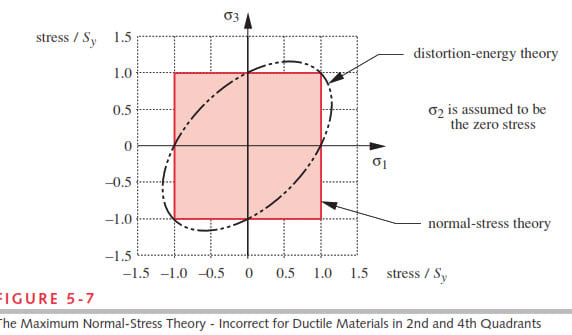
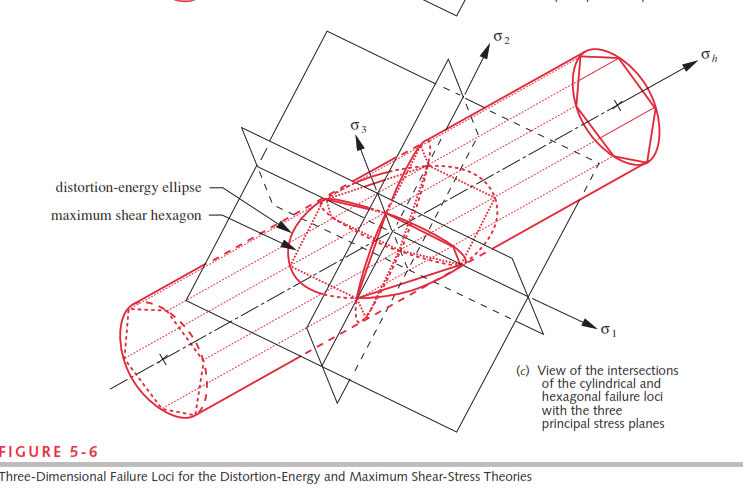
When do we use von mises stress and max principal stress in analyzing aerostructures? I got to know based on ductile and brittle materials we use.. but is there any other criteria to use. when subjected to tension compression or bending loads ? Which stress do we use or consider as critical ..
Thanks !
Thanks !