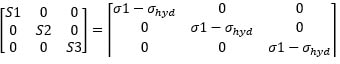At the end of the day these are just failure theories we attempt to correlate to test data. Reading a machine design book chapter on static failure theories will tell you a lot. I recommend Machine Design: An Integrated Approach by Robert Norton.
The most "accurate" failure theory, or which is conservative, depends on the actual state of stress.
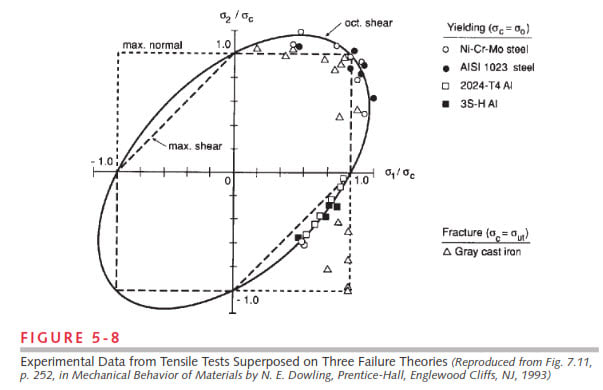
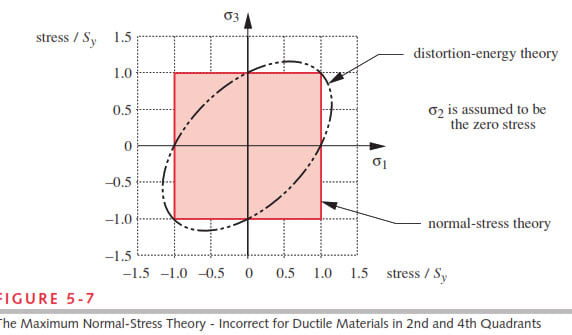
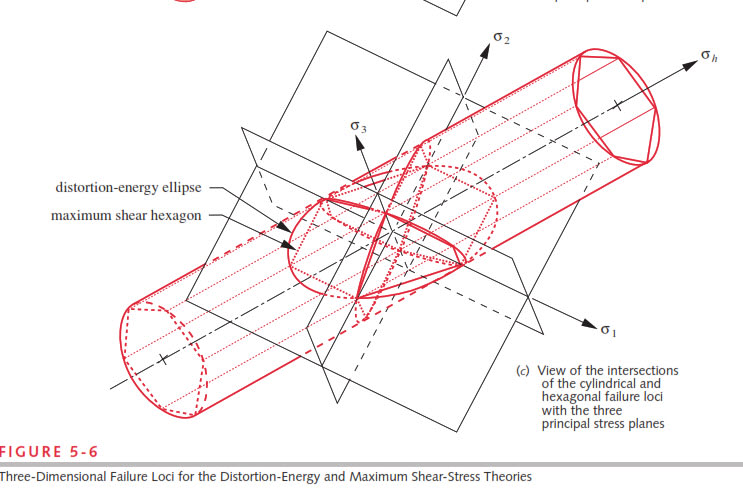
As I've said before on these forums (you can probably find a lot of posts about this exact topic if you search) - von Mises equivalent stress is just an equivalent uniaxial stress magnitude that causes the same shear distortion strain energy as the actual applied stress state, meant to be used with a typical uniaxial stress strain curve. The area below a typical stress strain curve represents the total strain energy absorbed. But we may recognize that the hydrostatic component of the strain energy contributes basically nothing to failure.
Actually the theory comes from Maxwell, Huber, Hencky, and von Mises independently.
The whole crux of what the various authors contribute is to take advantage of the fact that the second main invariant of the deviatoric stress tensor is always positive and can be assessed as a scalar value.
The theory is that the shear distortion strain energy (deviatoric strain energy) associated with change in shape of a stress element is key to material failure. The hydrostatic component contributes essentially nothing to failure. (And this is borne out by test data)
As such, for a complex stress state, we want a method of comparing deviatoric strain energy per unit volume to an imposed yield value. Von Mises “stress” does indeed have units of stress (intentionally) but is perhaps more rightly thought of as distortion strain energy per unit volume.
We can obtain this by starting with the stress deviator (deviatoric stress tensor) and imposing a condition relating to the distortion yield (pure shear yield stress) as follows:
J_2 is the second invariant of the stress deviator (simply the difference of the applied and hydrostatic stresses)
resulting in J_2=1/2*(S1^2+S2^2+S3^2 )
The criteria would then be f(J_2 )= √(J_2 )-k=0, where k is the pure shear yield strength such that when the complex stress deviator reaches this value, failure occurs. Herein lie the two biggest limitations of the theory
We will further on generally define k=σ_y/√3, so materials must approximate this. Also, F_ty and F_cy must be equal, otherwise we’d need to impose multiple values of k.
Huber pointed out that defining the effective stress as σ_eff=√(3*J_2 ) leads to the simple criteria 0= σ_eff - σ_y
Writing σ_eff with J_2 in terms of the principal or applied stresses and rearrangement leads to the well-known formulae for von Mises effective stress.
There are more "accurate" theories for uneven materials based on J2 and J3, but they are kind of "in the noise" of the test data anyway.
SWComposites said:
Max prin is often used for fatigue checks (max tensile stress) for metals
This is not inherently incorrect, but if I can add a little nuance... linear elastic fracture mechanics is specifically where you might see insistence on principal stress, because it is normally thought that cracks will grow perpendicular to this vector. Actually, cracks grow in he direction that maximizes strain energy release rate, so you can have slant cracks in mixed mode scenarios. But point taken. However:
1. We are usually making conservative envelopes that combine worst-case geometric correction and worst stress orientation anyway, and
2. For stress-life or strain-life, we are often dealing with multiaxial stress states, in which case most of the prevailing theories would have you work with an effective stress, NOT a principal stress.
Keep em' Flying
//Fight Corrosion!