DTS419
Structural
- Jun 21, 2006
- 180
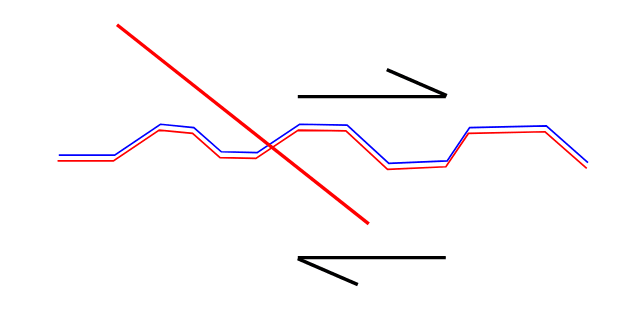
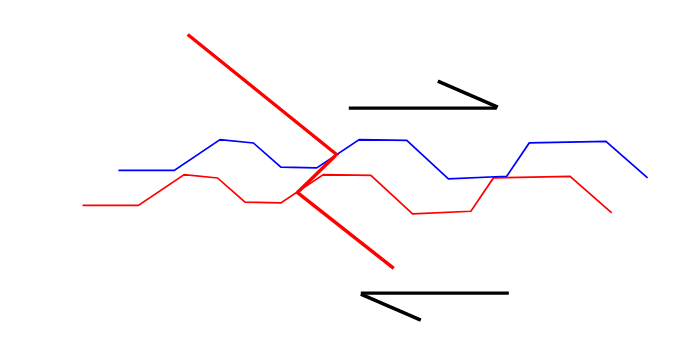
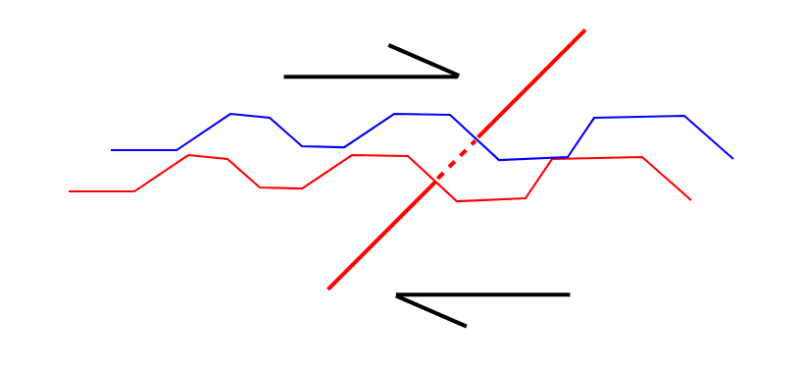
ACI 318-14 R22.9.4.3 says that shear friction does not apply when the reinforcing is angled so that it would be in compression and that as a rebuilt, Vn=0. This is counterintuitive as by inspection, the reinforcing angled up against the applied shear would be better. Why is Vn = 0 when the reinforcing is angled upward, and how would you determine the strength of this connection if in fact you had a case where the reinforcing was angled upward?