LowSpark
Electrical
- Jan 31, 2015
- 23
Hello All,
I have a question as to why every example of a beam splice shows the load in tension as shown in this link:
Kootk from this forum gave the solution to use a beam splice in this thread but no calculation example:
The only place I have found to talk about the load perpendicular to grain is this website which used a prescriptive approach:
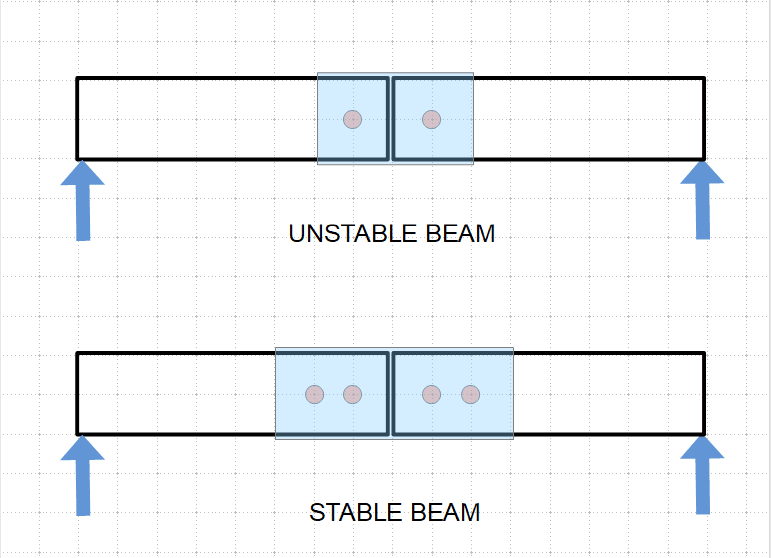
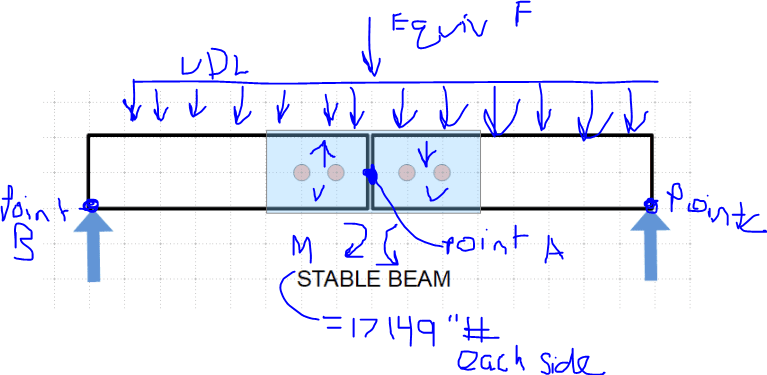
So my question is, why isn't there an example of the calculation shown in link one ( but with a uniform distributed load along the splice(such as the modified picture attached)?
I have a question as to why every example of a beam splice shows the load in tension as shown in this link:
Kootk from this forum gave the solution to use a beam splice in this thread but no calculation example:
The only place I have found to talk about the load perpendicular to grain is this website which used a prescriptive approach:
So my question is, why isn't there an example of the calculation shown in link one ( but with a uniform distributed load along the splice(such as the modified picture attached)?

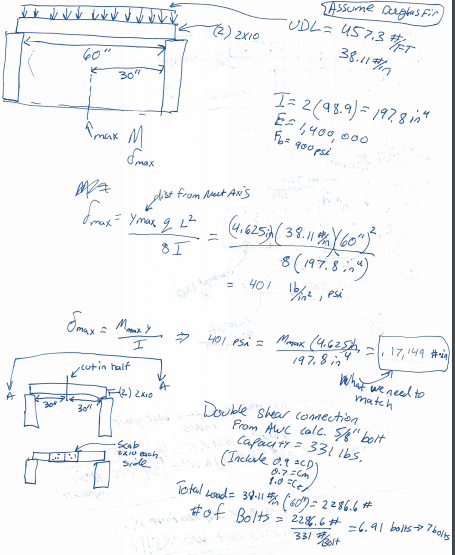
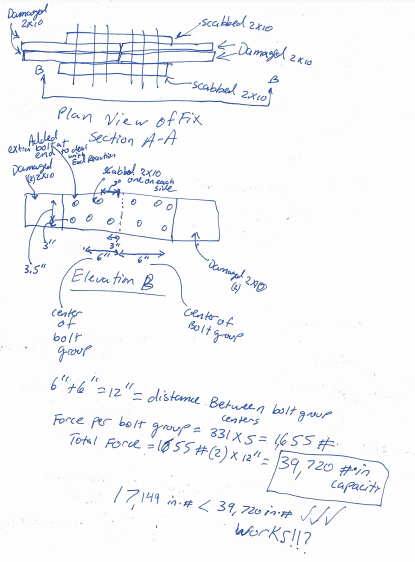
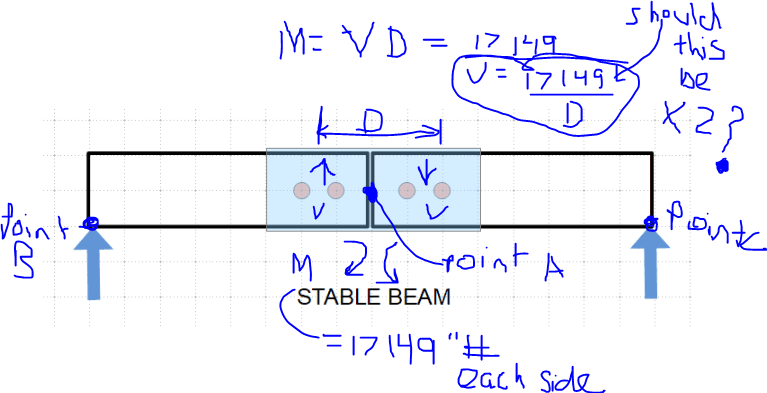
![[bigsmile] [bigsmile] [bigsmile]](/data/assets/smilies/bigsmile.gif) I want to make sure I understand what you mean, so I made up some numbers and tried to solve a sample situation. See attached sample problem where I try to get the needed moment capacity of the scab repair.
I want to make sure I understand what you mean, so I made up some numbers and tried to solve a sample situation. See attached sample problem where I try to get the needed moment capacity of the scab repair.