RichardWattMatrix
Computer
- Apr 19, 2021
- 24
Hello,
As described in my other thread ZK worm parameters, I am working with an existing software application that generates dressing programs for different types of threads and worms and I am currently working on fixing a reported issue with ZN type worms in the application.
So far, I have been able to produce a NC program for a Siemens 840Dsl CNC machine from calculated profiles, but whenever we grind a part on the machine, the profile has always been wrong, i.e., the flanks are more curved than we think they should be.
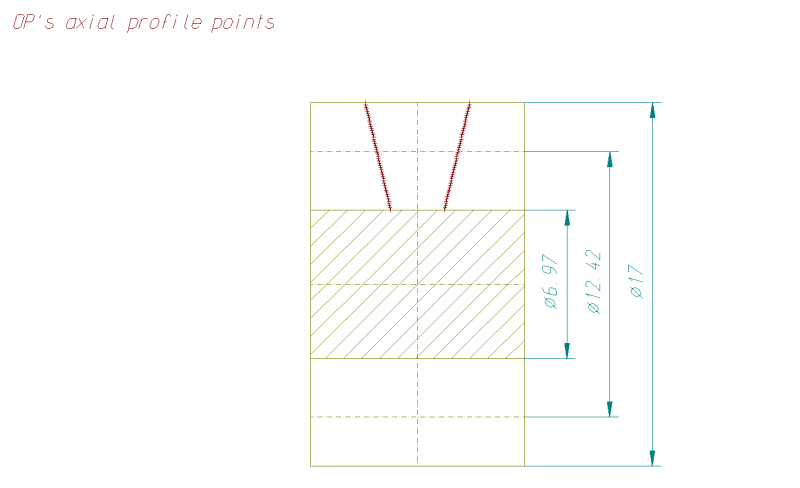
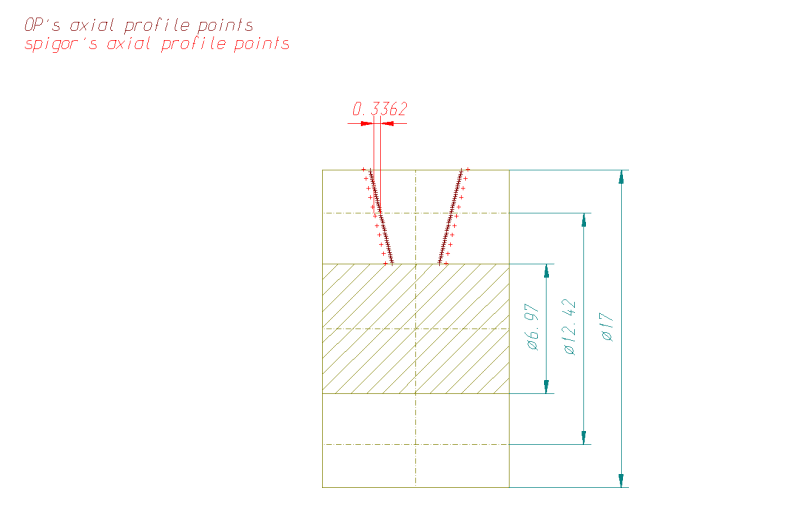
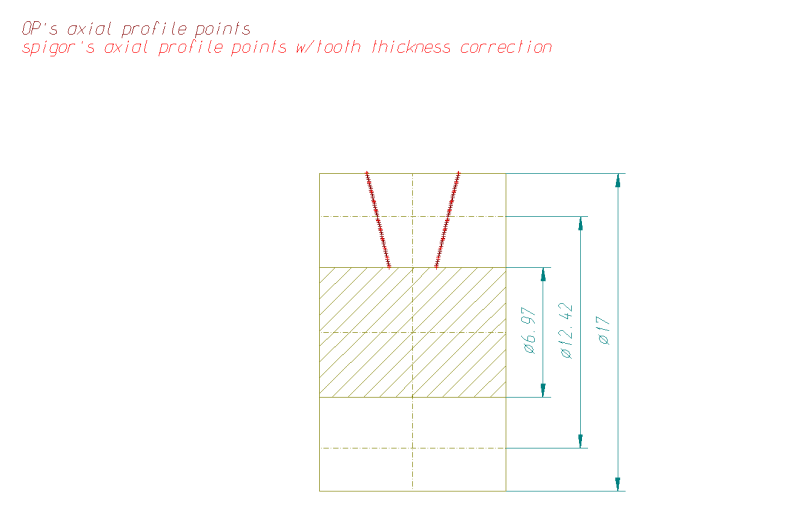
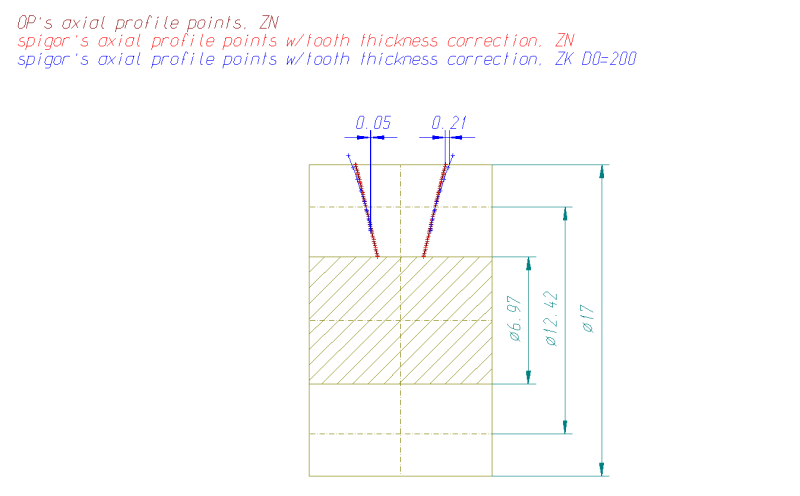
I have the data for 2 ZN worm parts provided by our customer who reported the issue and I have posted some of the details below for the first one:
[ul]
[li]Worm Type: ZN[/li]
[li]Number of teeth: 2[/li]
[li]Single lead[/li]
[li]Right handed[/li]
[li]Pitch circle diameter: 12.42 mm[/li]
[li]Tip diameter: 17 mm[/li]
[li]Root diameter: 6.97 mm[/li]
[li]Helix angle: 20.14 degrees[/li]
[li]Flank angle: 14.5 degrees (for both LH and RH)[/li]
[li]Lead: 14.311 mm[/li]
[li]Normal plane angle: 20.14 degrees[/li]
[li]Tip fillet radius: 0.5 mm[/li]
[li]Root fillet radius: 0.5 mm[/li]
[li]Measuring wire diameter: 4.7455 mm[/li]
[li]Size over the wires: 19.77 mm[/li]
[/ul]
We also have a setting that controls the number of points that are generated on the flanks, and this value is set to 50 in this case.
One thing I will point out is that we have a "Normal plane angle" parameter which we always set to the helix angle.
I also have copies of log files created by the software for the worm profiles on the normal and axial planes and I will attach them later as I cannot seem to do this from the office.
Edited to add normal (ZN_SingleLead_NormalPoints.Dat) file, which has the format of (I'll post the axial one in the next post):
[ol 1]
[li]No. - this is the point number[/li]
[li]Width(mm) - this is the profile width (X coordinate) for each point[/li]
[li]Radius(mm) - this is the profile radius (Y/Z coordinate) for each point[/li]
[li]Normal(deg) - this the angle from the X axis to the outward normal vector from this point[/li]
[li]Attribute - this is a point label identifying where the point is on the profile[/li]
[/ol]
I was wondering if someone could kindly help me generate the worm profiles (ideally both the normal and axial plane ones) and compare them against the attached result files please?
If there is any other information you need, please let me know.
Best regards,
Richard
As described in my other thread ZK worm parameters, I am working with an existing software application that generates dressing programs for different types of threads and worms and I am currently working on fixing a reported issue with ZN type worms in the application.
So far, I have been able to produce a NC program for a Siemens 840Dsl CNC machine from calculated profiles, but whenever we grind a part on the machine, the profile has always been wrong, i.e., the flanks are more curved than we think they should be.
I have the data for 2 ZN worm parts provided by our customer who reported the issue and I have posted some of the details below for the first one:
[ul]
[li]Worm Type: ZN[/li]
[li]Number of teeth: 2[/li]
[li]Single lead[/li]
[li]Right handed[/li]
[li]Pitch circle diameter: 12.42 mm[/li]
[li]Tip diameter: 17 mm[/li]
[li]Root diameter: 6.97 mm[/li]
[li]Helix angle: 20.14 degrees[/li]
[li]Flank angle: 14.5 degrees (for both LH and RH)[/li]
[li]Lead: 14.311 mm[/li]
[li]Normal plane angle: 20.14 degrees[/li]
[li]Tip fillet radius: 0.5 mm[/li]
[li]Root fillet radius: 0.5 mm[/li]
[li]Measuring wire diameter: 4.7455 mm[/li]
[li]Size over the wires: 19.77 mm[/li]
[/ul]
We also have a setting that controls the number of points that are generated on the flanks, and this value is set to 50 in this case.
One thing I will point out is that we have a "Normal plane angle" parameter which we always set to the helix angle.
I also have copies of log files created by the software for the worm profiles on the normal and axial planes and I will attach them later as I cannot seem to do this from the office.
Edited to add normal (ZN_SingleLead_NormalPoints.Dat) file, which has the format of (I'll post the axial one in the next post):
[ol 1]
[li]No. - this is the point number[/li]
[li]Width(mm) - this is the profile width (X coordinate) for each point[/li]
[li]Radius(mm) - this is the profile radius (Y/Z coordinate) for each point[/li]
[li]Normal(deg) - this the angle from the X axis to the outward normal vector from this point[/li]
[li]Attribute - this is a point label identifying where the point is on the profile[/li]
[/ol]
I was wondering if someone could kindly help me generate the worm profiles (ideally both the normal and axial plane ones) and compare them against the attached result files please?
If there is any other information you need, please let me know.
Best regards,
Richard