Hi all,
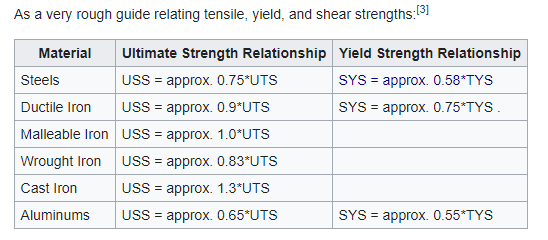
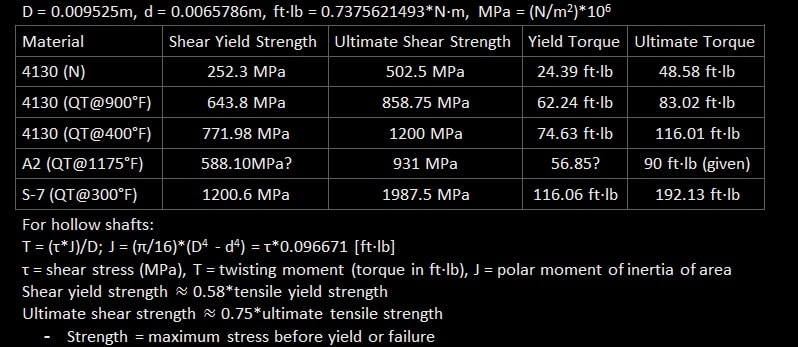
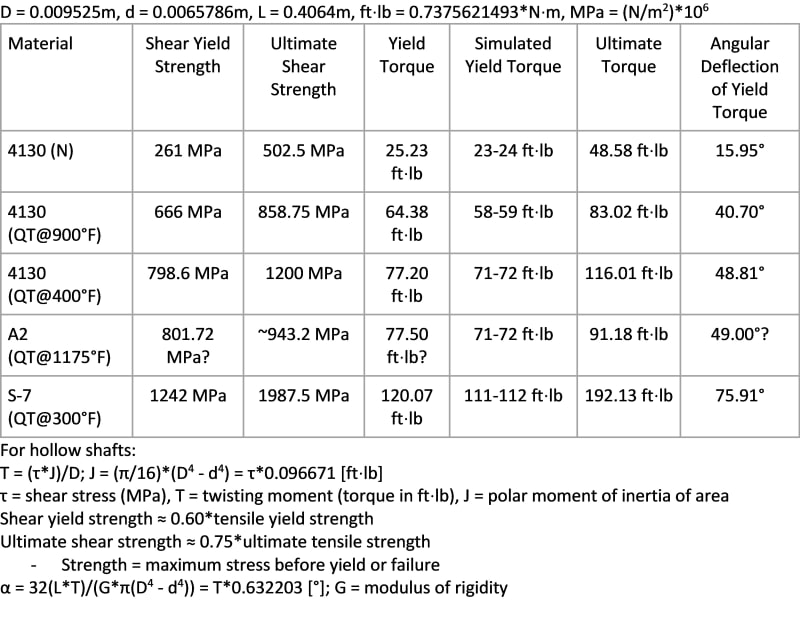
Do you know how I might go about calculating the maximum shear stress of a 16"-long, 0.375" OD x 0.259" ID Q&T 4130 tube? It has a yield strength of 1110MPa and ultimate tensile strength of 1145MPa. I am trying to calculate the maximum permissible torque that can be applied before yielding. If I approximate the shear stress as (1/sqrt(3)) * ultimate tensile strength, then the max torque comes out to 64ft-lbs. A SolidWorks simulation gives 58-59ft-lbs as the correct figure.
Thanks,
Jack
Do you know how I might go about calculating the maximum shear stress of a 16"-long, 0.375" OD x 0.259" ID Q&T 4130 tube? It has a yield strength of 1110MPa and ultimate tensile strength of 1145MPa. I am trying to calculate the maximum permissible torque that can be applied before yielding. If I approximate the shear stress as (1/sqrt(3)) * ultimate tensile strength, then the max torque comes out to 64ft-lbs. A SolidWorks simulation gives 58-59ft-lbs as the correct figure.
Thanks,
Jack