steel_plate_arch
Civil/Environmental
- Jun 19, 2020
- 4
Hello,
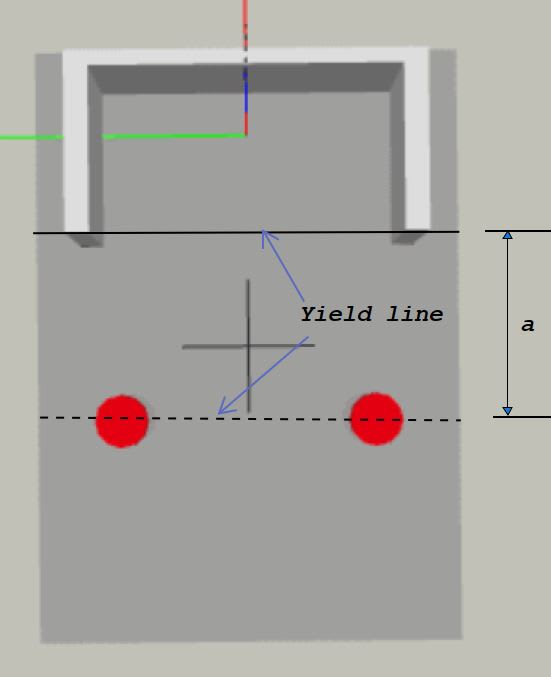
How exactly do I calculate the effective bending line on a base plate like shown below?
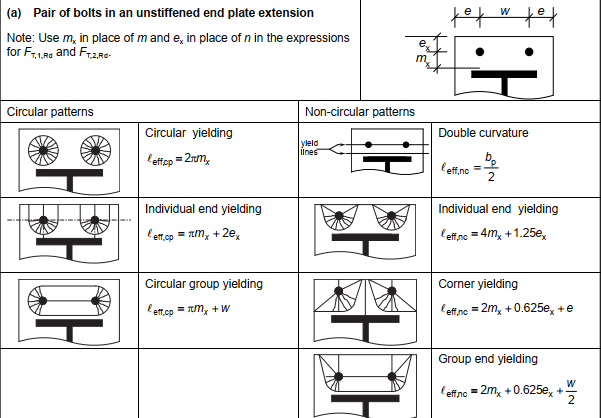
I've read that there are 45 degree projection lines that comes from the bolts. What about the farther bolt from the bend line? Is that one also projecting and therefore causes a larger line?
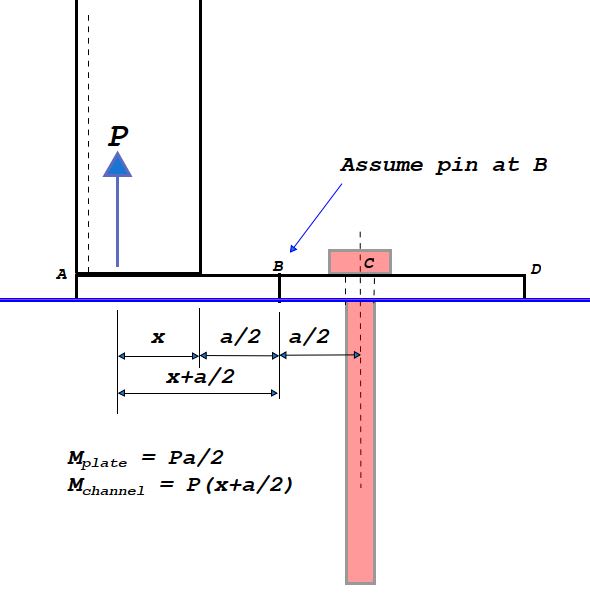
Visually I am having trouble determining how this bending line comes out to be. I've seen in another eng-tips post that also mentions including the perpendicular distance as well, so not sure about that one.
Hope someone can point me in right direction.Thanks.
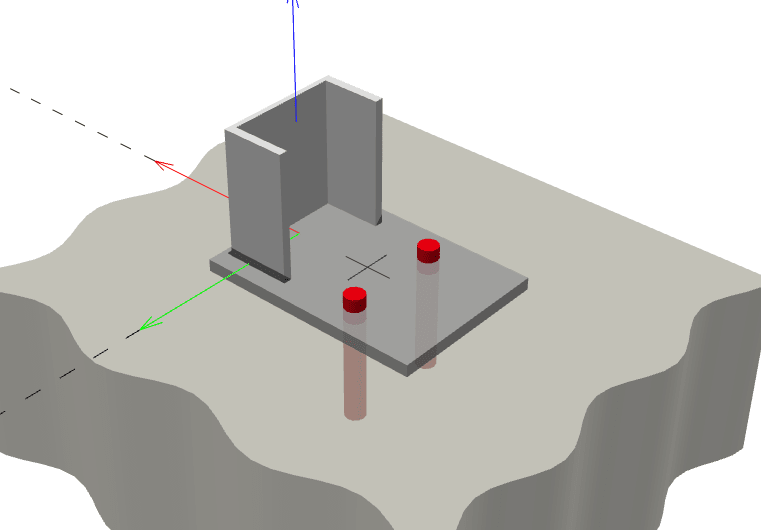
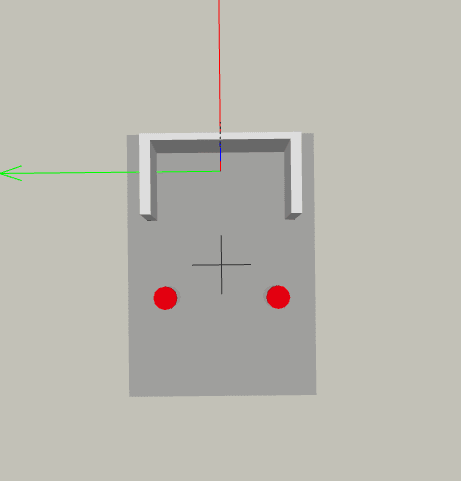
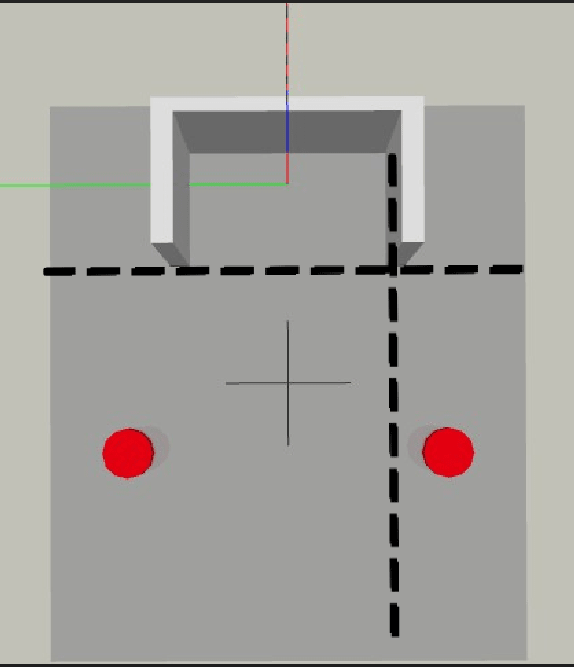
How exactly do I calculate the effective bending line on a base plate like shown below?
I've read that there are 45 degree projection lines that comes from the bolts. What about the farther bolt from the bend line? Is that one also projecting and therefore causes a larger line?
Visually I am having trouble determining how this bending line comes out to be. I've seen in another eng-tips post that also mentions including the perpendicular distance as well, so not sure about that one.
Hope someone can point me in right direction.Thanks.