Thank you all for your inputs.
The question does not mention about small deflections, but I think it just take it for granted. This assumption should be taken if needed.
It also feels right that the deflection should be in the direction of the force P. I just couldn’t properly explain (in detailed steps) why.
A quick check through, I may be missing something:
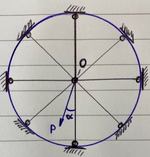
First, you have to assume "small deflections". Let x be the angle between force P and the spoke in question.
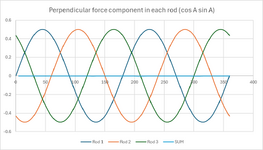
In that case, the deflection in each spoke will be cos(x) times the deflection in the direction of the force, and the component of force in each spoke, parallel to the force P, will be proportional to (cos(x))^2. Adding up the cosine-squared for N equally spaced spokes will give a constant, regardless of angle alpha. Example: Adding cosine squared for 20, 140, and 260 degrees is same as adding cosine squared for 30, 150, and 270 degrees, etc.
And, adding up the components of those same forces perpendicular to the force will give a cos(x)*sin(x) term for each spoke. And adding cosine x sine of 20, 140, 260 degrees gives zero. IE, the component of the spoke reactions normal to force P total up to zero, so deflection and force are always aligned.
JStephen, I like the reasoning, it seems right, but it still gives me some questions…
— “the component of the spoke reactions normal to force P total up to zero”… Wouldn’t that be the case from the start, considering that the resultant of the forces from the spokes should be directly oposite from P, for equilibrium? I’m not sure how to go from this to “deflection and force are always aligned”.
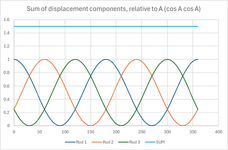
— “the deflection in each spoke will be cos(x) times the deflection in the direction of the force”… Let’s call Delta_P the deflection in the direction of the force P. So, Delta_P*cos(x) is the component of the Delta_P in the direction of the spoke. In the end, Delta_P will be indeed the full displacement of point O, but how to conclude that from the above?
You've drawn a bicycle wheel, so the empirical answer is yes.
Right. As I mentioned, it seems right the displacement is in line with the load in this case. But how to really prove that generally is the trick part for me…
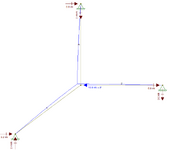
You can use vector algebra . Lets assume ( for simplicty ) n=4
In this case , the angles btw the spokes will be 90 degr. Then define a Cartesian coordinate system having the origin is at pt. O and , X and Y axis matching to the spikes.
Then define a force F having random angle ( α ) with X and find the components Fx and Fy.
-Fx is resisted by spikes on the X axis and one will have tension Fx/2 and the other compression Fx/2 and total displacement will be ( δx ) and for lineer elastic rods will be proportional to Fx taht is axial stiffness of the rod K= E*A and Fx= K*δx ,
-Fy is resisted by spikes on the Y axis and one will have tension Fy/2 and the other compression Fy/2 and total displacement will be ( δy) and for lineer elastic rods will be proportional to Fy that is axial stiffness of the rod K= E*A and Fy= K*δy ,
- Then draw the displacement vectors and find the resultant δ , which will have the same direction with force F .
Important point is ,number of spikes n must be at least 3. If n=2 , and the load is not parallel to spikes ,the system will be geometrically nonlinear ( although the spikes are lineer elastic )and the final displacement will not be parallel and proportional with the force .
That’s correct, but it’s not general… Considering 4 rods, the deflection of each rod (in the direction of the corresponding rod) is dependent on the angle, but the full displacement is not (you end up in a sum of sin2(x) with cos2(x)… I couldn’t work things out yet for 5 rods…
Suggest to use strain energy method
I’ll try that… I tried before like the following, but could not go further and conclude that the deflection is in the direction of P and its value does not depend on the angle…
For a truss with N rods, Strain energy U will be:
U = sum( (F_i^2) * L / (2EA) ), with i from 1 to N
From here, I could differentiate U with respect to P, and find the displacement in direction of P… but from here, how to conclude that this is the full displacement of the node O?
Thanks again for your insights.