-
4
- #1
NedGan76
Structural
- Apr 4, 2022
- 36
Hi, everyone!
Here is an interesting and funny statics problem, to exercise engineering brains and cheer up.
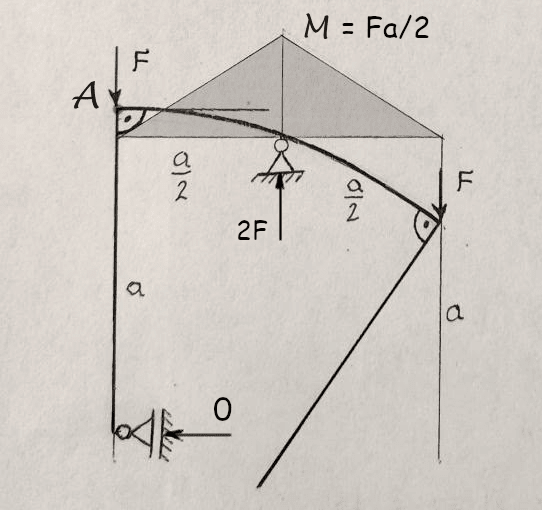
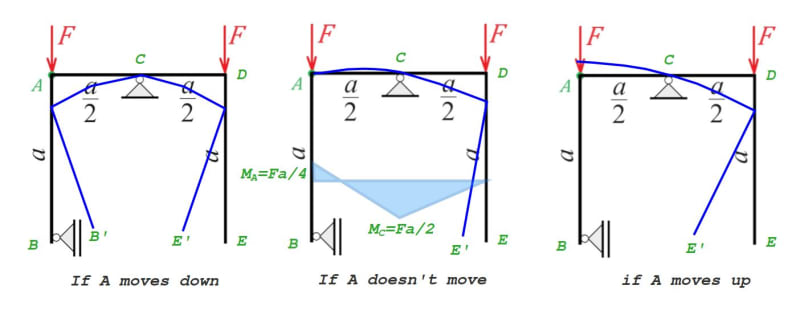
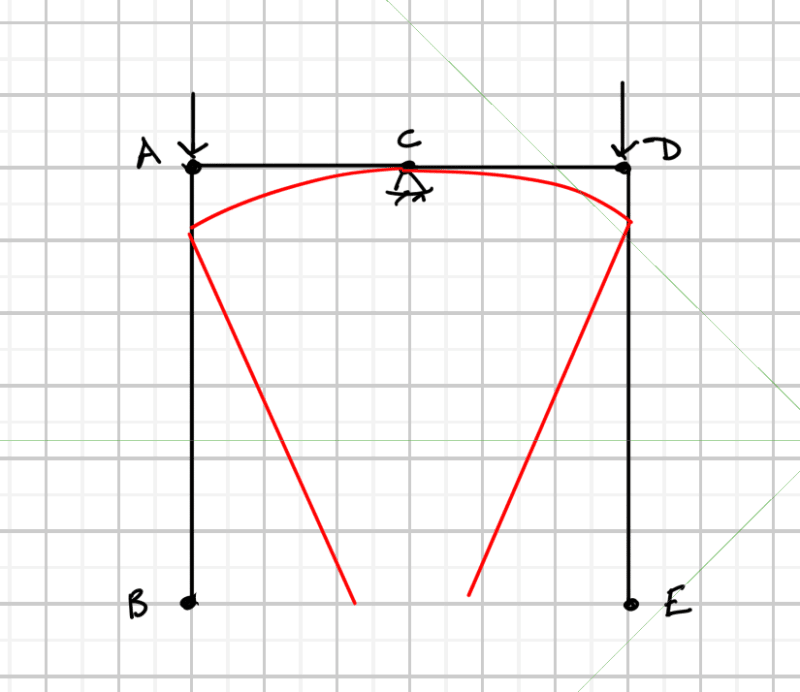
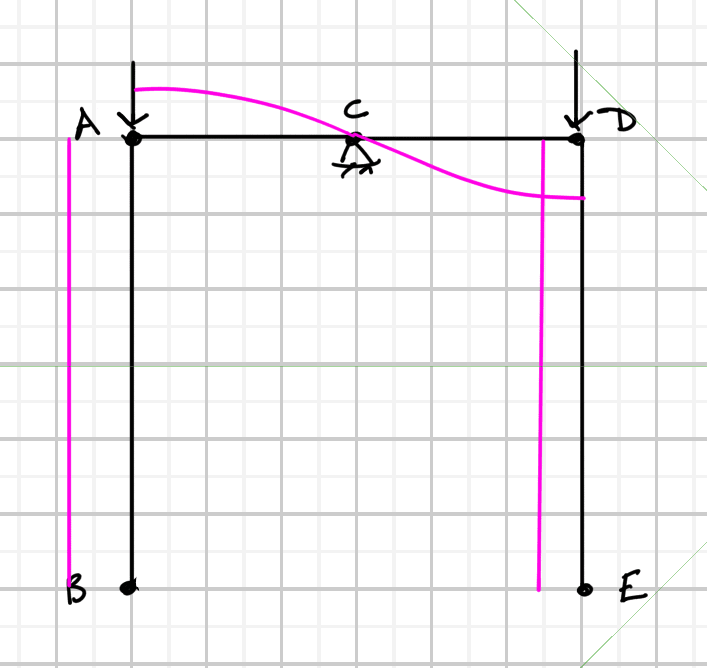
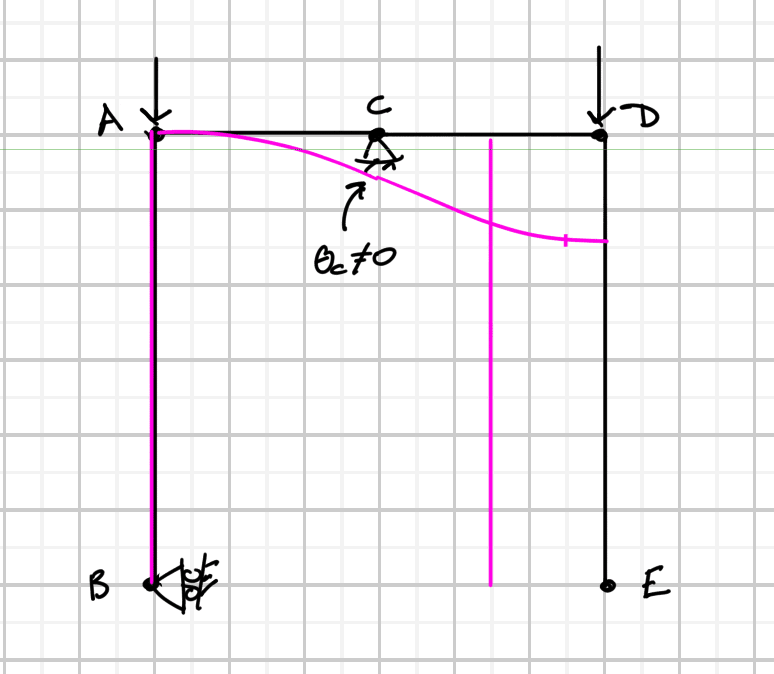
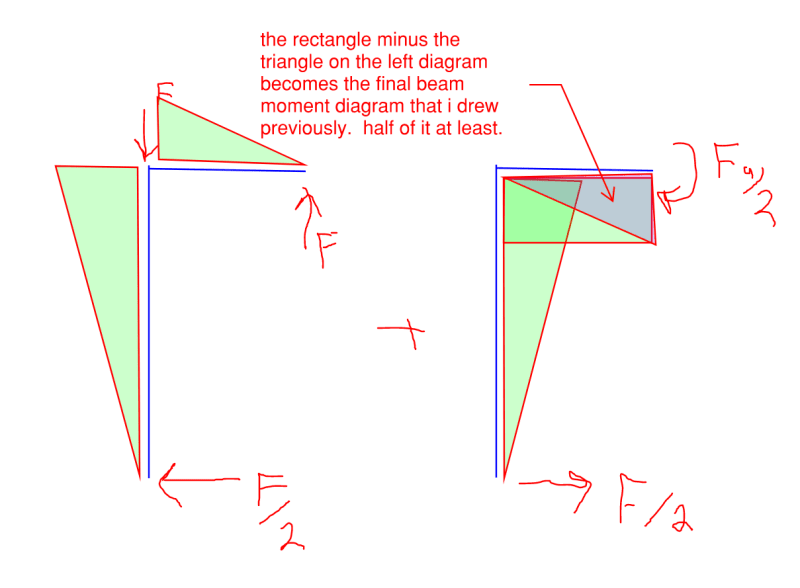
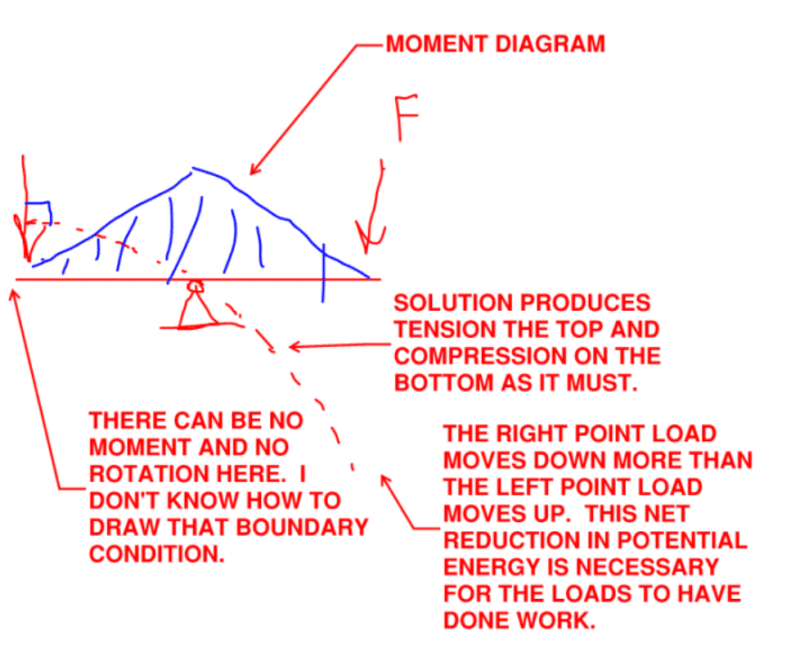
Given the following structure can you tell, without calculating, in which direction point A will move after deformation:
A) up
B) down
C) will not move
... and why? Point A is not a hinge. No structural analysis programs allowed.
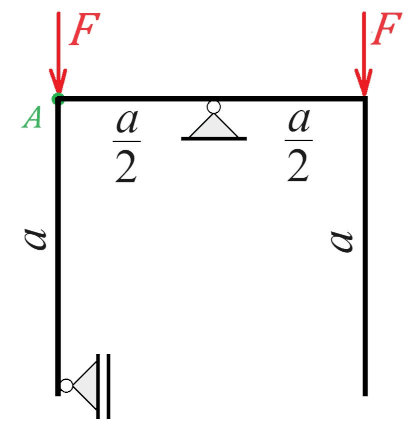
Here is an interesting and funny statics problem, to exercise engineering brains and cheer up.
Given the following structure can you tell, without calculating, in which direction point A will move after deformation:
A) up
B) down
C) will not move
... and why? Point A is not a hinge. No structural analysis programs allowed.






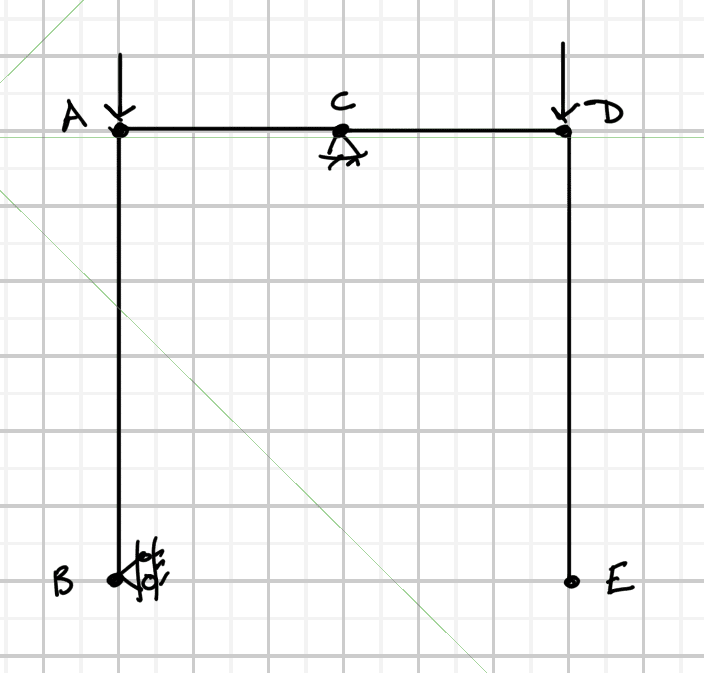
![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)