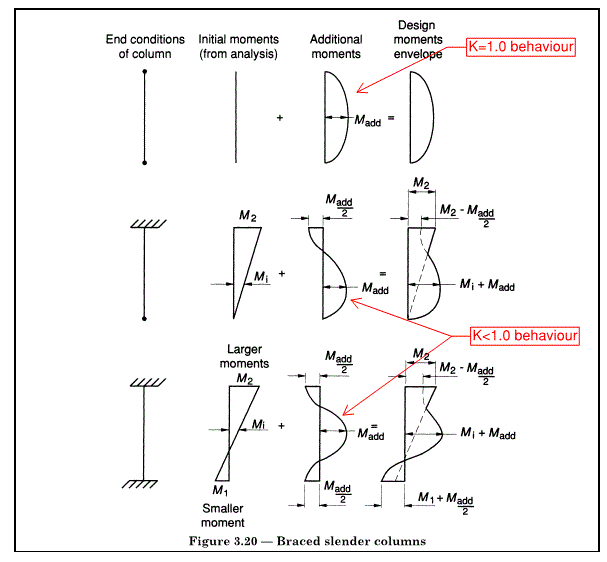
-
2
- #1
One thing that I've often been curious about is the buckling behaviour of a nominally pinned column under compression with a typical 'pinned' base plate.
Examples:
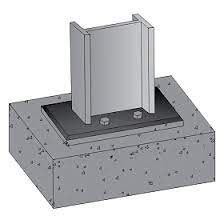
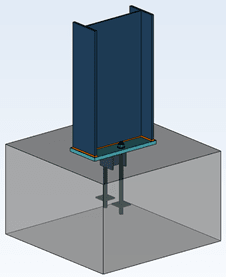
For both of these I would consider these as 'pinned' connection and model them as such. Thus I'd would get zero moment transfer and effectively length of 1 if top of the column is braced but with no rotational restraint. As I understand it this is a pretty typical analysis approach under most codes and in most jurisdictions.
My question is:
Is this overly conservative? Would the compression and flat base plate not provide a degree of fixity and thus improve the critical buckling load? Here I define here a baseplate that is resting on a foundation but not restrained from uplift as a SEPPERABLE BASE PLATE.
It would surprise me if there isn't already plenty of literature on this matter. But I've never seen it. So I'd though I'd test it. And since I don't have a test laboratory at hand I figure I'd use FEA.
TEST APPROACH
-Non-linear plastic FEA analysis using NASTRAN
-Tri linear model of stress-strain curve used
-Iterative approach to converge on buckling solution (NASTRAN does have non-linear buckling analysis but not nonlinear PLASTIC buckling analysis)
-An additional lateral load of 1% of axial load was added to trigger the buckling. (This value is arbitrary but considered reasonable and conclusions not sensitive to this.)
TEST DETAILS
-Steel section: HEB160 S275 (EUROPEAN STEEL)
-Section length: 6600mm
-Minor axis translationally fixed, translationally fixed at the top, rotationally free.
-Base plate modelled in 3 ways; perfectly pinned; able separate but not slide AND; rigidly connected to foundation.
-Nominal mesh size - 50mm
CODE BUCKLING LIMIT:
Ncx = ~780kN (without any capacity reduction factor, both codes AS4100 and Eurocode within 2%)
FEA RESULTS
PINNED: Ncx = ~800kN
BASE PLATE (with sepparation): Ncx =~1150kN (equivalent le = 0.83)
BASE PLATE (RIGID): Ncx =~1150kN (equivalent le = 0.83)
As can be seen no discernible difference (<1% tolerance) between the rigidly connected base plate and a base plate with no uplift restraint.
CONCLUSION
In some/many circumstances it is not unreasonable to consider a typical column and base plate arrangement as 'fixed' for consideration of its buckling effective length. Without doing exhausting further testing I would suggest that this is reasonably representative for columns of 'intermediate slenderness' where inelastic buckling dominates.
ADDITIONAL TESTING
I was a little perturbed by the lack of discernible difference between a rigidly fixed base plate and one that is able to separate from its support. I hypothesised that this was due to inelastic buckling dominating before any appreciable rotation could occur at the base. This was tested by doubling the length of the HEB160 to 13200mm. To summarise this additional testing:
PINNED BASE = 275kN (Unreduced capacity in code 250kN)
BASE PLATE ON SURFACE = 460kN (equivalent le = 0.77)
FIXED BASE PLATE = 500kN (equivalent le = 0.74)
It was satisfying to see that for more slender columns the back calculated effective length approached the theoretical Euler elastic theoretical length. It was also satisfying to confirm that a fully fixed base base does exhibit better performance (as expected) compared to a separable base plate.
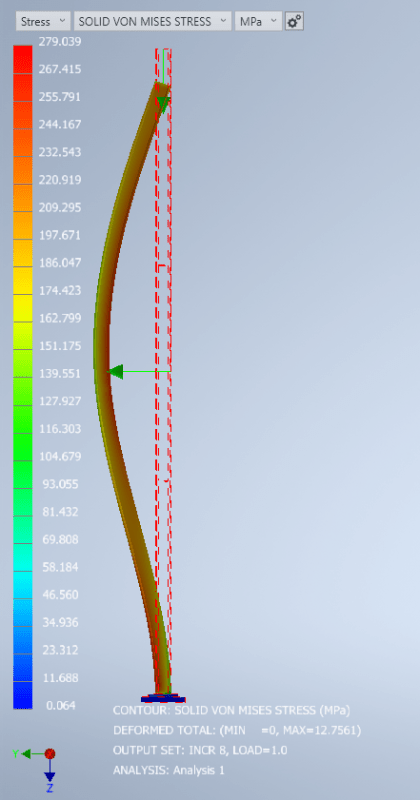
And here is a pretty FEA picture to keep everybody happy:
Examples:


For both of these I would consider these as 'pinned' connection and model them as such. Thus I'd would get zero moment transfer and effectively length of 1 if top of the column is braced but with no rotational restraint. As I understand it this is a pretty typical analysis approach under most codes and in most jurisdictions.
My question is:
Is this overly conservative? Would the compression and flat base plate not provide a degree of fixity and thus improve the critical buckling load? Here I define here a baseplate that is resting on a foundation but not restrained from uplift as a SEPPERABLE BASE PLATE.
It would surprise me if there isn't already plenty of literature on this matter. But I've never seen it. So I'd though I'd test it. And since I don't have a test laboratory at hand I figure I'd use FEA.
TEST APPROACH
-Non-linear plastic FEA analysis using NASTRAN
-Tri linear model of stress-strain curve used
-Iterative approach to converge on buckling solution (NASTRAN does have non-linear buckling analysis but not nonlinear PLASTIC buckling analysis)
-An additional lateral load of 1% of axial load was added to trigger the buckling. (This value is arbitrary but considered reasonable and conclusions not sensitive to this.)
TEST DETAILS
-Steel section: HEB160 S275 (EUROPEAN STEEL)
-Section length: 6600mm
-Minor axis translationally fixed, translationally fixed at the top, rotationally free.
-Base plate modelled in 3 ways; perfectly pinned; able separate but not slide AND; rigidly connected to foundation.
-Nominal mesh size - 50mm
CODE BUCKLING LIMIT:
Ncx = ~780kN (without any capacity reduction factor, both codes AS4100 and Eurocode within 2%)
FEA RESULTS
PINNED: Ncx = ~800kN
BASE PLATE (with sepparation): Ncx =~1150kN (equivalent le = 0.83)
BASE PLATE (RIGID): Ncx =~1150kN (equivalent le = 0.83)
As can be seen no discernible difference (<1% tolerance) between the rigidly connected base plate and a base plate with no uplift restraint.
CONCLUSION
In some/many circumstances it is not unreasonable to consider a typical column and base plate arrangement as 'fixed' for consideration of its buckling effective length. Without doing exhausting further testing I would suggest that this is reasonably representative for columns of 'intermediate slenderness' where inelastic buckling dominates.
ADDITIONAL TESTING
I was a little perturbed by the lack of discernible difference between a rigidly fixed base plate and one that is able to separate from its support. I hypothesised that this was due to inelastic buckling dominating before any appreciable rotation could occur at the base. This was tested by doubling the length of the HEB160 to 13200mm. To summarise this additional testing:
PINNED BASE = 275kN (Unreduced capacity in code 250kN)
BASE PLATE ON SURFACE = 460kN (equivalent le = 0.77)
FIXED BASE PLATE = 500kN (equivalent le = 0.74)
It was satisfying to see that for more slender columns the back calculated effective length approached the theoretical Euler elastic theoretical length. It was also satisfying to confirm that a fully fixed base base does exhibit better performance (as expected) compared to a separable base plate.
And here is a pretty FEA picture to keep everybody happy: