I have an existing structure I'm analyzing and I'm just not matching something. It's a parking deck, live load = 40 psf. Beam is 20" wide x 26" deep, pan joist system is 6" side x 18" deep with 4" slab (6" x 14" + 4" slab). The Beam span is 57' and the tributary width is 28'. The effective prestress force is 350 kips. At the center of the beam positive auxiliary rebar consists of 2#5 and 2#6 bars. At the support negative auxiliary rebar consists of 3#7 and 2#8 bars. I'm getting a capacity of 712 k-ft positive and 872 k-ft negative. I am getting a DEMAND of 630 k-ft positive and 1262 k-ft negative. This can't be right. I'm just checking the existing loads, I haven't put the proposed loads or anything on there. d=23.75". I'm not sure what I'm missing, I may be burnt out and missing something to simple that I may be booted from the forum but any help would be greatly appreciated.
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Existing Post tension beam doesn't meet what the existing loads would require 4
- Thread starter jplay2519
- Start date
- Status
- Not open for further replies.
KootK said:All I really stated initially is that PT drape helps resists load and should be accounted for in some fashion, which is obvious. Otherwise, we wouldn't have the Golden Gate bridge to admire.
hokie66 said:So, I take it that you have accepted that ultimate strength computations are not affected by drape, at least in the context of prestressed concrete?
Yes. Previously, I mentioned the example of the Golden Gate bridge. I thought that a salient example at the time. In order to get my world view fully adjusted, I feel it necessary to answer my own questions regarding that example. What was missing there, I think, was
a) a proper appreciation of the self-equilibrating nature of Pe & Balancing loads and;
b) Recognition that the PT anchorage situation is markedly different for the golden gate bridge.
To clarify, I've sketched up:
a) A fictional version of the Golden Gate that is more like a PT beam, where drape doesn't matter and;
b) A fictional version of a PT beam that is more like the Golden gate bride, where drape matters.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
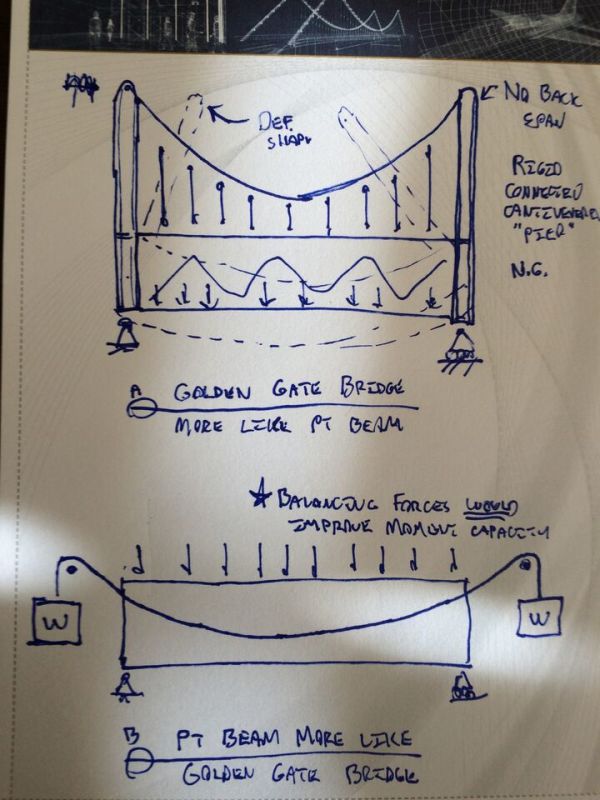
hokie said:A prestressing strand in a pretensioned member, with the strand flat, provides the same ultimate capacity as a draped strand of the same size and with the same effective depth.
That is true at midspan, but the flat strand provides greater ultimate capacity at every other point in the span than the draped strand.
It should also be noted that the flat strand provides greater camber than a draped strand with the same maximum effective depth.
BA
So, based on the information presented in my last few posts, the relationship between load balancing effects and ultimate strength is as follows:
Load balancing effects are present in the ultimate condition and affect the ultimate strength that we count on. However, those load balancing effects are perfectly offset by the the moments generated by the anchorage forces acting on the member. The net effect on ultimate load carrying capacity is that there is no effect at all.
My original, flawed, assumption was that load balancing effects were assisting with load resistance in the ultimate state but were ignored as matter of choice / conservatism. Statements like those shown below have contributed to my misunderstanding. They make somewhat more sense to me now that my understanding has evolved some.

You see variations of this a lot in the literature. Load balancing effects are used to resist load in the ultimate state. They're just offset by other effects. Our procedures for calculating ultimate bending capacity account for all that but, unfortunately for me, do not make that accounting transparent. So, really, the salient point in the above statement should really be to not account for the load balancing effects twice (rapt's point somewhere above.

Again, this statement gives me the false impression that load balancing effects represent a capacity improvement that has been deliberately left on the table. Perhaps it's a matter of terminology that's resulted in my confusion with with this one.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
Load balancing effects are present in the ultimate condition and affect the ultimate strength that we count on. However, those load balancing effects are perfectly offset by the the moments generated by the anchorage forces acting on the member. The net effect on ultimate load carrying capacity is that there is no effect at all.
My original, flawed, assumption was that load balancing effects were assisting with load resistance in the ultimate state but were ignored as matter of choice / conservatism. Statements like those shown below have contributed to my misunderstanding. They make somewhat more sense to me now that my understanding has evolved some.

You see variations of this a lot in the literature. Load balancing effects are used to resist load in the ultimate state. They're just offset by other effects. Our procedures for calculating ultimate bending capacity account for all that but, unfortunately for me, do not make that accounting transparent. So, really, the salient point in the above statement should really be to not account for the load balancing effects twice (rapt's point somewhere above.

Again, this statement gives me the false impression that load balancing effects represent a capacity improvement that has been deliberately left on the table. Perhaps it's a matter of terminology that's resulted in my confusion with with this one.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
@hokie: does mean that:
1) You reviewed my diatribe and agree with every scrap of it or;
2) You noticed that I noticed that I was wrong and you're happy to leave it at that?
I'm hoping that it's the former.
I just stepped ofo of my elliptical machine and realized that I'm screwed again. If Pe moments offset load balancing effect moments at all locations, then there's no net curvature change and therefore no "lift" in the slab. And that can't be right.
Really, I'm just getting started. I suspect that there's much more ground to be covered once I try to extend these same principles to continuous members.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
1) You reviewed my diatribe and agree with every scrap of it or;
2) You noticed that I noticed that I was wrong and you're happy to leave it at that?
I'm hoping that it's the former.
I just stepped ofo of my elliptical machine and realized that I'm screwed again. If Pe moments offset load balancing effect moments at all locations, then there's no net curvature change and therefore no "lift" in the slab. And that can't be right.
Really, I'm just getting started. I suspect that there's much more ground to be covered once I try to extend these same principles to continuous members.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
Well. Done. Elliptical's actually driving me a little nuts. It gets me up close to some TJI's that have apparently been flange cut to deal with unwanted continuity. I frickin' hate that. Separate thread to follow.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
KootK said:If Pe moments offset load balancing effect moments at all locations, then there's no net curvature change and therefore no "lift" in the slab. And that can't be right.
Upon further consideration, moments due to Pe and balancing effects only cancel out when moments are taken about the tendon axis. For other locations, like the section centroid, balancing loads effects will remain uncancelled and impacting curvature so as to generate lift.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
KootK,
A tendon draped in a parabolic curve, when stressed, will exert a uniform uplift on the concrete member. That is what T.Y. Lin meant by load balancing. One difference between a prestressed tendon and a freely suspended cable is that the tendon relies on the member to supply the horizontal reaction whereas the cable relies on external reactions.
If the concrete starts to crush at midspan, the stress in the tendon can no longer be sustained and the member fails. That is why load balancing cannot contribute to ultimate load.
BA
A tendon draped in a parabolic curve, when stressed, will exert a uniform uplift on the concrete member. That is what T.Y. Lin meant by load balancing. One difference between a prestressed tendon and a freely suspended cable is that the tendon relies on the member to supply the horizontal reaction whereas the cable relies on external reactions.
If the concrete starts to crush at midspan, the stress in the tendon can no longer be sustained and the member fails. That is why load balancing cannot contribute to ultimate load.
BA
BA Retired said:A tendon draped in a parabolic curve, when stressed, will exert a uniform uplift on the concrete member.
No argument there. That's kinda where I started.
BA Retired said:One difference between a prestressed tendon and a freely suspended cable is that the tendon relies on the member to supply the horizontal reaction whereas the cable relies on external reactions.
Just like my Golden Gate bridge sketches above, right?
BARetired said:If the concrete starts to crush at midspan, the stress in the tendon can no longer be sustained and the member fails. That is why load balancing cannot contribute to ultimate load.
This may sound odd given my recent difficulties but I disagree. You know... tepidly.
Per the sketch that I posted above, and have repeated below, I believe that the balanced load effects are implicitly built into our procedure for ultimate moment capacity. If you removed the load balancing effects, ultimate bending capacity would need to be reduced as a as result.
Logically, if concrete crushing meant that we could no longer rely on the tension in the tendon, all that we'd be left with for moment capacity would be the portion attributed to the non-prestressed reinforcement. And that certainly isn't reflected in our procedure for determining ultimate flexural capacity.
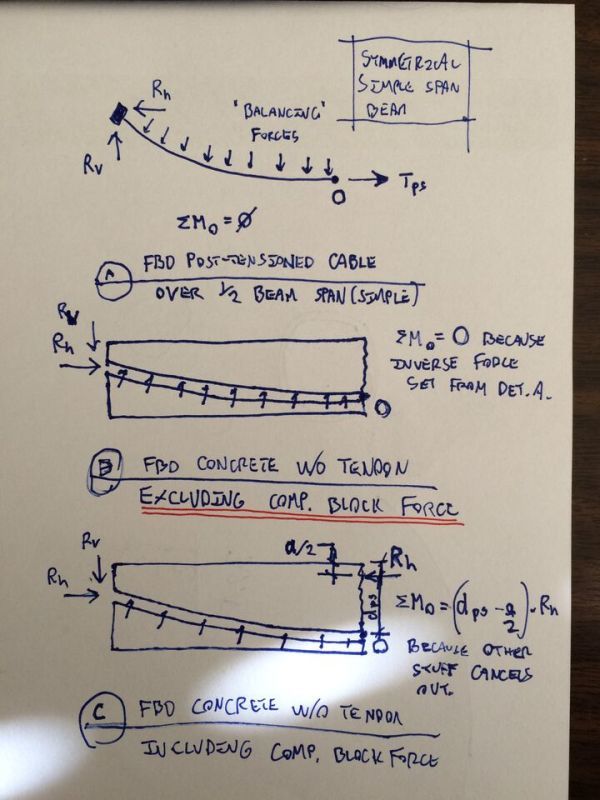
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
KootK said:Per the sketch that I posted above, and have repeated below, I believe that the balanced load effects are implicitly built into our procedure for ultimate moment capacity. If you removed the load balancing effects, ultimate bending capacity would need to be reduced as a result.
If the tendons are flat, i.e. without drape, at the same effective depth as you show at midspan, the prestress force would then be applying an equal and opposite moment at each end of the member, namely P.e which would cause an upward deflection of PeL/8EI; if you call that load balancing, then the load it is balancing is a uniform moment across the span without external reactions, not a gravity load balancing.
If the tendons are flat at the neutral axis, there would be no balancing of any kind but the ultimate moment capacity would still be the ultimate tendon force times the depth to the middle of the stress block.
BA
@BA: I would consider the flat tendon scenario to be a unique, and obviously somewhat trivial, case of load balancing where the equivalent balanced load is zero. That said, I still believe that the derivation that I posted above would apply as follows:
1) With no tendon curvature, the transverse balancing load effect would be non-existent and thus it would create no moment about point O.
2) The horizontal anchorage force would also create no moment about point O because the anchorage and point O would be vertically aligned.
3) The vertical anchorage force would be zero and thus also create no moment about point O.
4) All summed, we again have a self-equilibrated M=0 system in which the net effect of the balanced load forces and anchorage forces on ultimate moment is no effect at all. And, if that's correct, it would be great as a universally applicable principle is the most confidence inspiring kind in my opinion.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
1) With no tendon curvature, the transverse balancing load effect would be non-existent and thus it would create no moment about point O.
2) The horizontal anchorage force would also create no moment about point O because the anchorage and point O would be vertically aligned.
3) The vertical anchorage force would be zero and thus also create no moment about point O.
4) All summed, we again have a self-equilibrated M=0 system in which the net effect of the balanced load forces and anchorage forces on ultimate moment is no effect at all. And, if that's correct, it would be great as a universally applicable principle is the most confidence inspiring kind in my opinion.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
Word, words and more words. I was responding to the following:
The procedure for determining ultimate moment capacity in a prestressed member is identical to that of a conventionally reinforced member and has nothing to do with balanced load effects.
Why would ultimate bending capacity need to be reduced if the load balancing effects were removed? Can you provide an example of that?
BA
KootK said:Per the sketch that I posted above, and have repeated below, I believe that the balanced load effects are implicitly built into our procedure for ultimate moment capacity. If you removed the load balancing effects, ultimate bending capacity would need to be reduced as a as result.
The procedure for determining ultimate moment capacity in a prestressed member is identical to that of a conventionally reinforced member and has nothing to do with balanced load effects.
Why would ultimate bending capacity need to be reduced if the load balancing effects were removed? Can you provide an example of that?
BA
BA said:The procedure for determining ultimate moment capacity in a prestressed member is identical to that of a conventionally reinforced member and has nothing to do with balanced load effects.
The procedure does not involve balanced load effects but that's only because they cancel out. The mechanism by which ultimate loads are resisted does involve balanced load effects, however, per my derivation.
BA said:Why would ultimate bending capacity need to be reduced if the load balancing effects were removed?
To see the effect, take my detail C above and remove the balanced load effect. To maintain equilibrium, the moment resistance would decrease by the amount that the balanced load effect previously contributed to the system.
BAretired said:Can you provide an example of that?
No, because it's not possible. That was the 'proof' that I proposed with details A and B. The balancing effects and anchorage forces form a self-equilibrating system that has no net effect on ultimate moment capacity. I'm not suggesting that we need to change our method for calculating ultimate flexural capacity. I'm simply clarifying that a) our procedure assumes that balancing forces are alive and kicking in the ultimate condition b) load balancing forces are in fact alive and kicking in the ultimate condition.
BA said:Word, words and more words
You're preaching to the choir. And nobody's posted more graphical supporting material here than me. All of my latest arguments have been predicated on my derivation (A/B/C) being correct. It was my hope that it would be more fruitful for folks to debate the validity of that underlying, graphical derivation rather than debate the consequences of that derivation. I really am trying to reduce extraneous wordsmithing.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
@jplay: Until recently, I'd forgotten about the VSL post-tensioned concrete guides. I thought that you might enjoy them. First off, taken together, they constitute a pretty solid free reference on PT. More importantly, the PT possibilities that they illustrate are pretty inspiring in my opinion. I'm not sure how much of the fancy stuff actually comes to pass but it's pretty dang cool none the less. My PT experience has been limited to pretty mundane stuff (slabs/beams/transfers/tanks).
VSL Slabs
VSL Buildings
VSL Foundations
VSL Detailing
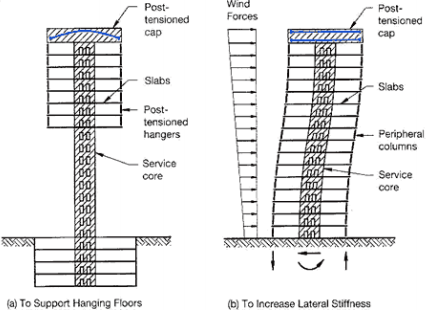

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
VSL Slabs
VSL Buildings
VSL Foundations
VSL Detailing


I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
-
1
- #58
Kootk,
We all have bad days!
Prestressing by itself creates a self-equilibrating stress state. In a weightless member, the centroid of the prestress force (tension) will be the same as the centroid of the compression force in the concrete at any point along the member and in a determinate member, that will be at e from the centroid where e is the tendon eccentricity from the concrete centroid. Thus there is no "lever arm" between the compression and tension forces. For an indeterminate member, it will be offset from e by Msec / P.
The concept of "balanced load" is simply a method of visualizing and calculating the effects of the change in tendon curvature. Yes, it induces a curvature in the member, equivalent to the moment from the balanced load = wl^2/8 and this is exactly equal to P.e. They are simply 2 methods of calculating the same thing. In some texts they are not called balanced loads, they are called Equivalent Loads (eg Gilberts book) which is less misleading! Leonhardt, while developing the formula for an upward load u = V 8 f / L^2 for the calculation of prestressing effects does not even give it a name as far as I can tell, just suggesting that it makes the calculation of the prestressing effects much more simple than calculating the eccentricities of a parabolic tendon.
For complicated cable profiles and where the Prestress force varies significantly, calculating P.e and using curvatures to calculate the secondary prestress effects is a lot easier as there may not be a logical balanced load profile.
Once you have the theoretical weightless system with P and C at the same height, as you then add load, the compression zone changes and its centroid moves away from the pure prestress position creating a lever arm. As more and more load is added, it eventually cracks the concrete (assumed 0 tensile strength for crack control and ultimate calculations) and the compression centroid moves up further increasing the lever arm even more. At the same time the force in the tendon is increasing due to either strain compatibility for bonded PT or due to the elongation of the whole tendon for unbonded. So you have an increasing P and an increasing lever arm as you continue to add load. Eventually it gets to the ultimate condition and you have the maximum stress you are going to get in the tendons (and any other reinforcement) and the maximum lever arm possible and this gives you your ultimate strength.
We all have bad days!
Prestressing by itself creates a self-equilibrating stress state. In a weightless member, the centroid of the prestress force (tension) will be the same as the centroid of the compression force in the concrete at any point along the member and in a determinate member, that will be at e from the centroid where e is the tendon eccentricity from the concrete centroid. Thus there is no "lever arm" between the compression and tension forces. For an indeterminate member, it will be offset from e by Msec / P.
The concept of "balanced load" is simply a method of visualizing and calculating the effects of the change in tendon curvature. Yes, it induces a curvature in the member, equivalent to the moment from the balanced load = wl^2/8 and this is exactly equal to P.e. They are simply 2 methods of calculating the same thing. In some texts they are not called balanced loads, they are called Equivalent Loads (eg Gilberts book) which is less misleading! Leonhardt, while developing the formula for an upward load u = V 8 f / L^2 for the calculation of prestressing effects does not even give it a name as far as I can tell, just suggesting that it makes the calculation of the prestressing effects much more simple than calculating the eccentricities of a parabolic tendon.
For complicated cable profiles and where the Prestress force varies significantly, calculating P.e and using curvatures to calculate the secondary prestress effects is a lot easier as there may not be a logical balanced load profile.
Once you have the theoretical weightless system with P and C at the same height, as you then add load, the compression zone changes and its centroid moves away from the pure prestress position creating a lever arm. As more and more load is added, it eventually cracks the concrete (assumed 0 tensile strength for crack control and ultimate calculations) and the compression centroid moves up further increasing the lever arm even more. At the same time the force in the tendon is increasing due to either strain compatibility for bonded PT or due to the elongation of the whole tendon for unbonded. So you have an increasing P and an increasing lever arm as you continue to add load. Eventually it gets to the ultimate condition and you have the maximum stress you are going to get in the tendons (and any other reinforcement) and the maximum lever arm possible and this gives you your ultimate strength.
@rapt:
As far as the raw facts go, I agree with all of your last post. It is consistent with, and is a natural extension of, the derivation that I presented above (details A/B/C). What I still disagree with, somewhat, is the perspective taken. Everything that follows will be stated with unbonded PT in mind, to the extent that does or doesn't matter.
To me, this implies that Pxe is the real physical phenomenon and balanced load effects are a convenient construct for "visualizing and calculating the effects of the change in tendon curvature". I believe that it's the other way round: the balanced load effect is really and truly applying transverse load to the member, in service and at ultimate, and it is Pxe that is the convenient construct for visualization and calculation.
At the ends of a member, the center of compression starts off at the anchorages. The physical action that shifts the center of compression to coincide with the tendons as we move along the length of a member is the balancing load effect. That's what gets it done as it were.
At the start of this thread, I was trying to double dip with regard to the balancing load. And that was wrongheaded. However, I still find statements to the effect of "balancing loads have nothing to do with ultimate flexural capacity" to be rather misleading. I believe that what people really mean, or should mean, when they make such statements, is:
1) Our standard calculation procedure does not explicitly include balancing load effects and/or;
2) Balancing load effects should be included once in the formulation, not twice.
Were it not for the balancing load effects, when we calculated ultimate flexural capacity of a member, the post-tensioning force would have to be located at the elevation of the anchorages rather than at the elevation of the tendon. Viewed in that sense, the balancing load effects have a significant impact on ultimate flexural capacity.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
As far as the raw facts go, I agree with all of your last post. It is consistent with, and is a natural extension of, the derivation that I presented above (details A/B/C). What I still disagree with, somewhat, is the perspective taken. Everything that follows will be stated with unbonded PT in mind, to the extent that does or doesn't matter.
rapt said:The concept of "balanced load" is simply a method of visualizing and calculating the effects of the change in tendon curvature...and this is exactly equal to P.e. They are simply 2 methods of calculating the same thing.
To me, this implies that Pxe is the real physical phenomenon and balanced load effects are a convenient construct for "visualizing and calculating the effects of the change in tendon curvature". I believe that it's the other way round: the balanced load effect is really and truly applying transverse load to the member, in service and at ultimate, and it is Pxe that is the convenient construct for visualization and calculation.
At the ends of a member, the center of compression starts off at the anchorages. The physical action that shifts the center of compression to coincide with the tendons as we move along the length of a member is the balancing load effect. That's what gets it done as it were.
At the start of this thread, I was trying to double dip with regard to the balancing load. And that was wrongheaded. However, I still find statements to the effect of "balancing loads have nothing to do with ultimate flexural capacity" to be rather misleading. I believe that what people really mean, or should mean, when they make such statements, is:
1) Our standard calculation procedure does not explicitly include balancing load effects and/or;
2) Balancing load effects should be included once in the formulation, not twice.
Were it not for the balancing load effects, when we calculated ultimate flexural capacity of a member, the post-tensioning force would have to be located at the elevation of the anchorages rather than at the elevation of the tendon. Viewed in that sense, the balancing load effects have a significant impact on ultimate flexural capacity.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
Kootk,
Just trying to make sure I understand what you are suggesting, so I will go through what I think your steps are
If we assume a single determinate span of length L and a rectangular section of depth D with the prestress force P anchored at mid depth. And then the tendon drapes down by the amount e parabolically to midspan from each end.
Assume the compression centroid depth at ultimate is dc and prestress force increases by deltaP at ultimate to be P + deltaP.
We will forget about capacity factors etc at this stage, assume they are 1 for ease of calculation.
balanced load = wp = 8 P e / L^2
1 Calacuate capacity at end of span at the anchorage
M*anch = (P + deltaP) * (D/2 - dc) (basically Tension force * lever arm)
2 Calculate capacity at midspan
M*midspan = M*anch + wp l^2 / 8
Is this what you are suggesting?
Just trying to make sure I understand what you are suggesting, so I will go through what I think your steps are
If we assume a single determinate span of length L and a rectangular section of depth D with the prestress force P anchored at mid depth. And then the tendon drapes down by the amount e parabolically to midspan from each end.
Assume the compression centroid depth at ultimate is dc and prestress force increases by deltaP at ultimate to be P + deltaP.
We will forget about capacity factors etc at this stage, assume they are 1 for ease of calculation.
balanced load = wp = 8 P e / L^2
1 Calacuate capacity at end of span at the anchorage
M*anch = (P + deltaP) * (D/2 - dc) (basically Tension force * lever arm)
2 Calculate capacity at midspan
M*midspan = M*anch + wp l^2 / 8
Is this what you are suggesting?
- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 9
- Views
- 9K
- Question
- Replies
- 5
- Views
- 8K
- Question
- Replies
- 1
- Views
- 6K
- Replies
- 12
- Views
- 10K
- Replies
- 3
- Views
- 649

![[elephant2] [elephant2] [elephant2]](/data/assets/smilies/elephant2.gif) the elliptical machine
the elliptical machine