Existing Post tension beam doesn't meet what the existing loads would require 4

[jplay2519]

I have an existing structure I'm analyzing and I'm just not matching something. It's a parking deck, live load = 40 psf. Beam is 20" wide x 26" deep, pan joist system is 6" side x 18" deep with 4" slab (6" x 14" + 4" slab). The Beam span is 57' and the tributary width is 28'. The effective prestress force is 350 kips. At the center of the beam positive auxiliary rebar consists of 2#5 and 2#6 bars. At the support negative auxiliary rebar consists of 3#7 and 2#8 bars. I'm getting a capacity of 712 k-ft positive and 872 k-ft negative. I am getting a DEMAND of 630 k-ft positive and 1262 k-ft negative. This can't be right. I'm just checking the existing loads, I haven't put the proposed loads or anything on there. d=23.75". I'm not sure what I'm missing, I may be burnt out and missing something to simple that I may be booted from the forum but any help would be greatly appreciated.

 

[KootK]

We're the CIA, not the Mafia...But personally I tend to say what I think, rather than based on the country of origin of whoever I am responding to.

I don't doubt it. However, you fellows do tend to:

1) Travel as a pack.
2) Get real excited about long term concrete deflections and bonded prestress.
3) Generally support one another.

It's not a bad thing. Quite the opposite. If there were a Canuck Sons of Aggregate MC, I'd sign up in a bloody heartbeat.

On this particular thread, I'm not even sure what the point of contention is now.

That's an easy one. The point of contention is whether or not balancing load effects have any bearing on member ultimate flexural capacity. Although, that said, I feel like that topic has borne about as much fruit as it's likely to. I'm now more interested in other related topics... like the effect of drape. FYI: OP gave me explicit permission to hijack his thread a some time ago.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[Ingenuity]

KootK,

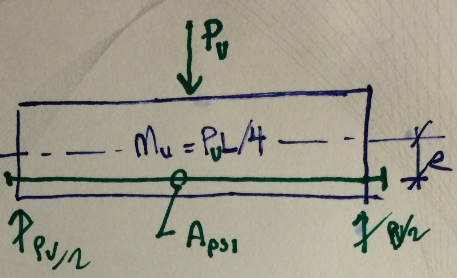
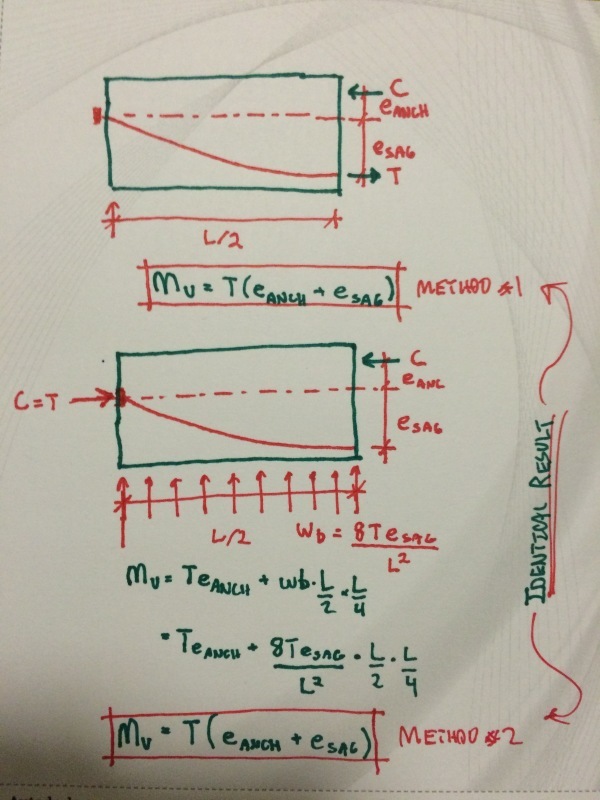
Detail 1 and Detail 2 of your sketches directly above have identical flexural moment DEMANDS at ultimate. The drape does not change the demand.

Detail 2 has more favorable flexural SERVICE stresses in the concrete compared to Detail 1, under external midpsan load of P, including equivalent loads due to prestress.

Your M/V diagrams are at SERVICE level loads under the action of EXTERNALLY applied load P, PLUS prestress. These M/V diagrams are not correct at ULTIMATE conditions.

 

[rapt]

Kootk,

Thinking back to an earlier reply of yours above, you related all of this to the Golden Gate Bridge. That is a suspension structure. A cable structure.

A PT member, bonded or unbonded, is not designed as a cable structure, it is designed as a flexural member. Basically a reinforced concrete member with steel in it that has an initial tension in it when connected to the concrete.

In the case of an unbonded tendon, that steel does not have strain compatibility with the concrete around it, hence the reason why ACI requires a large amount of bonded streel to be added to make the member act like a flexural member in the post-cracking load range. Otherwise it would act like a cable structure once the concrete cracked and go into catenary action, which would not be nice for a flexural member.

In your last post above, you still have net M and V = 0 for the draped cases! That would imply that the ultimate applied moments have been negated by the prestress.

PS Of the 6 main people who have replied to this post, the 'Aussie Mafia", I think only 2 are Australian born and trained, and of those one has been living and working in Canada and USA and USA Territories for about the last 20 years. Two others are now living in Australia but were born and trained in USA and UK respectively for the majority of their engineering lives and I think the other 2 are fully USA. So it looks like I am the Mafia, though I am in the CIA with IDS!

 

[Ingenuity]

I don't doubt it. However, you fellows do tend to:

1) Travel as a pack.
2) Get real excited about long term concrete deflections and bonded prestress.
3) Generally support one another.

Interestingly, hokie66 appears to be a US-educated engineer (Virginia Tech) who has practiced in Australia. RAPT and IDS are Australia-based but with international experiences (UK and Middle East?), and myself I was educated in Australia, and have practiced in Sydney, Canada for a few years, before moving to the US more than 20 years ago.

So quite a cross-section of experiences amongst the 'pack', Eh!

 

[rapt]

Ingenuity,

Now I am going to disagree with you (a little)

1 & 2 have identical flexural moment CAPACITY and DEMANDS at ultimate AT MIDSPAN.

1 has the same capacity at all points as it does at midspan, so it has excess capacity as you move away from midspan where there is reducing demand.

2 has reducing capacity as you move away from midspan as the effective depth of the tendon reduces but still more than demand.

RE service stresses,
1 and 2 have the same service performance at midspan.

1 has better service stress performance on the bottom away from midspan (more negative effect from the prestress as it is constant as you move away from midspan) but possible transfer stress problems in the top towards the support due to the tension in the top caused by the eccentric prestress at the supports.

Kootk
3 is definitely better as a continuous member always is better. But the Area of prestress required will not be less than Aps1 / 2, it will be equal to Aps1 / 2 as the moments will be halved for the arrangement you have defined.

In a Simply supported beam, raising the anchorages at the end above the concrete centroid will not increase the balancing effect as the eccentric anchorages will induce an applied +ve effective moment at each end at the ends exactly equal to the expected increase in balancing effect of the harped profile, completely negating the increase expected (reverse to the effect you have shown for the straight tendon at the ends).

 

[Ingenuity]

1 & 2 have identical flexural moment CAPACITY and DEMANDS at ultimate AT MIDSPAN.

I agree, but I did only state that the DEMANDS are the same. And they are the same DEMANDS at similar locations for both Detail 1 and Detail 2, along the full span.

RE service stresses,
1 and 2 have the same service performance at midspan.

1 has better service stress performance on the bottom away from midspan (more negative effect from the prestress as it is constant as you move away from midspan) but possible transfer stress problems in the top towards the support due to the tension in the top caused by the eccentric prestress at the supports.

For the 'theoretical' case referenced (fixed point load at midpsan) the Detail 2 stresses better 'balance' the load vs prestress, leaving only P/A, but I get your point.

 

[jplay2519]

Great discussion guys. I'm trying to get some classes and software so I can dig more into this and learn more about PT. I'm following most of the conversation and appreciate it. Since I'm not well versed in PT it's good to see both sides and to see both sides answer the responses.

@Kootk Thanks for the documentation. I'll be using those in my learning as well.

 

[KootK]

Fine. The next time that I'm toiling away in a thread and the Australian Concrete Mafia (ACM) shows up, I'll immediately switch my internal label to the Multicultural Concrete Mafia All Having Significant Ties to the Australian Subcontinent (MCMAHSTAS). The acronym's a bit ungainly but, hey, whatever it takes to maintain political correctness.

Detail 1 and Detail 2 of your sketches directly above have identical flexural moment DEMANDS at ultimate. The drape does not change the demand. Your M/V diagrams are at SERVICE level loads under the action of EXTERNALLY applied load P, PLUS prestress. These M/V diagrams are not correct at ULTIMATE conditions.

In your last post above, you still have net M and V = 0 for the draped cases! That would imply that the ultimate applied moments have been negated by the prestress.

I believe that you may have misinterpreted my sketches. If you read the titles carefully (my hand writing sucks), my diagrams are net actions on the concrete alone. Obviously, I agree that nothing, including tendon drape, changes the actual demand on the member as a whole. However, the presence of the tendons and their drape does effect the ultimate moment and shear applied to the concrete, examined in isolation. My idea with the sketches was to confirm my understanding that tendon drape effectively moves load from the point of application the columns without really involving the concrete. I suppose that I've implicitly examined a hypothetical case where 100% of the ultimate loads have been balanced. In a real member, the balancing would be less than that but similar principles would still apply.

You guys keep coming back to permutations of AT SERVICE LOADS. I find it strange as I take the following to be self-evident:

1) Draped tendons apply transverse forces to the concrete.
2) #1 is as true in the ultimate condition as it is at serviceability. Perhaps a little more so.

Are we not in agreement on these basics?

Thinking back to an earlier reply of yours above, you related all of this to the Golden Gate Bridge. That is a suspension structure. A cable structure. A PT member, bonded or unbonded, is not designed as a cable structure, it is designed as a flexural member.

I debunked the golden gate analogy myself above. That's what my sketch on the subject was about. I see the fundamental difference being the fact that, with the bridge, the cables are not anchored to the beam element but, rather to something external. I agree that PT members are not designed as cable structures. But, in many respects, I believe that they could be.

Early in this thread, I discovered a significant flaw in my thinking. To correct that, I've basically reevaluated PT member behavior from the ground up, starting with statics. As such, I don't want the particulars of "how we design PT concrete" to cloud my developing understanding of "what is the fundamental character of PT concrete". I feel that has been a problem with regard to the focus on the service state versus the ultimate state. It's the same damn balancing load effect at work in both states. The only difference is our procedural handing of the effect at service versus ultimate.

3 is definitely better as a continuous member always is better. But the Area of prestress required will not be less than Aps1 / 2, it will be equal to Aps1 / 2 as the moments will be halved for the arrangement you have defined.

I figured that it would be slightly less than half because the concrete stress block depth would be reduced. It sort of depends on whether or not your looking at it from a balancing load perspective or a conventional ultimate moment capacity perspective though. For 100% balancing, it would be half exactly. For ultimate flexural capacity, a little less than that. I'm still having trouble reconciling the two for indeterminate structures. It's... complicated. Either way, it's a minor point I think.

In a Simply supported beam, raising the anchorages at the end above the concrete centroid will not increase the balancing effect as the eccentric anchorages will induce an applied +ve effective moment at each end at the ends exactly equal to the expected increase in balancing effect of the harped profile, completely negating the increase expected (reverse to the effect you have shown for the straight tendon at the ends).

Yup. That was exactly the point of my derivation (detals A&B) on October 25th. Frankly, I've been a bit surprised that nobody's expressed any real interest in that. While I've no doubt that it's out there someplace, I've not yet seen another general proof of the concept. Most people and publications seem to just state it as fact and leave it that. At the risk of tooting my own horn, I thought that my proof was rather clever, particularly given that it requires next to no mathematics.

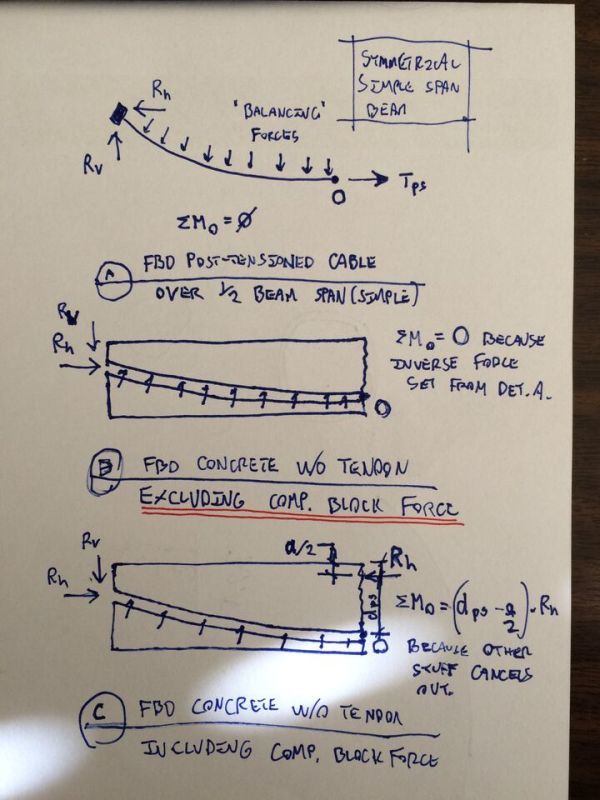
In detail B below, I've examined the equilibrium of the concrete without the PT tendon and, importantly, without the compression block reaction at the section cut. Because the forces that the tendon impose on the concrete are the inverse of those imposed by the concrete on the tendon, I again take the moment summation about point O to be zero. I propose this as non-rigorous proof (to myself) that balancing forces and anchorage reactions form a self-equibrilating system that, taken in concert, do nothing to improve bending capacity.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[IDS]

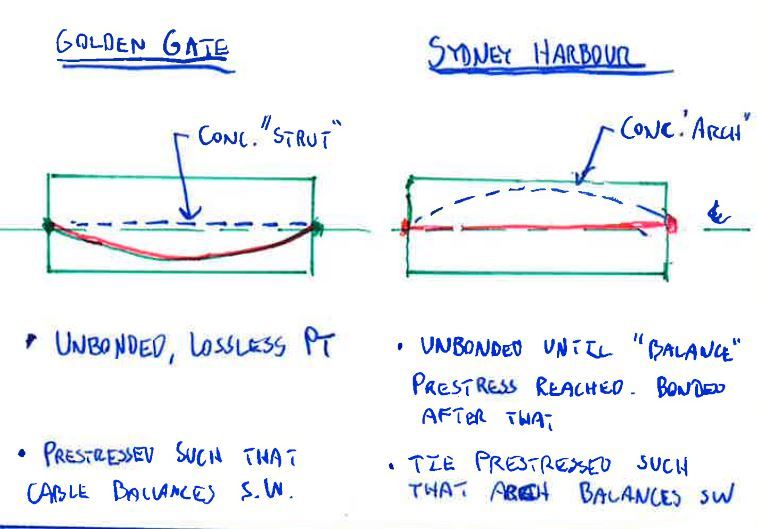
I think the GGB analogy is actually still useful, because after the cables have been anchored to the concrete (with the patented zero-loss anchoring system) the structure becomes an ordinary post-tensioned beam (except for the zero friction ducts) with balanced loads. Also it clarifies the difference between the draped system and the horizontal cable system with Infinite Debonding System (patent applied for). The latter system I will now call the Sydney Harbour Bridge system, because if you started off with an unreinforced concrete beam with external horizontal restraints at the bottom it would carry the load in arching. If you then replaced the external restraint with horizontal tendons (with IDS) you would end up with a prestressed beam with horizontal tendons.

The differences and similarities between the two structures are:

[ol 1]
[li]In both the bending moment in the concrete is the same at every section (zero).[/li]
[li]The axial force in the concrete is constant in the GGB system and varying from zero at the ends to same as GGB at mid-span in the SHB system.[/li]
[li]In the GGB the shear forces are carried entirely through the tendons, but in the SHB the shear forces are carried entirely through the concrete (in arching, rather than through shear deformation).[/li]
[/ol]

An important point (I think) is that you can only balance one load, but at this load the two structures are both acting as balanced load mechanisms. The only difference is that in the GGB the shear forces are carried by catenary action in the steel, and in the SHB the shear is carried by arching in the concrete.

For any increased load the moment is carried entirely by bending stresses in the concrete in a draped debonded system (because the tendon force does not increase), or jointly by the concrete and increased force in the tendons in a bonded system. In both cases the increased shear is carried through the concrete.

I think this is consistent with what everybody has said, but if not, please let me know.


p.s. Strictly speaking, Australia is a continent, not a sub-continent.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[rapt]

Kootk,

Mafia back again. Still do not see that discussion in your Oct 25 posts but we will leave that one.

OK, so we are now purely discussing "Equivalent Balanced Load" effects, under the prestress force at the time of stressing. Not due to any other forces induced in the tendon due to applied loads causing member curvature and increases in tendon force! And not looking at section capacity or member capacities.

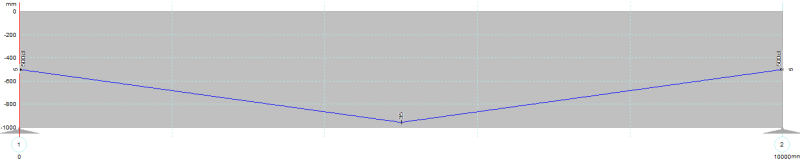
The tendons in the 2 diagrams below will result in the same equivalent balanced load effects, though one has a perfectly straight tendon and one has a harped tendon!

That is because the equivalent load is NOT simply caused by the change in slope of the tendon. It is caused by the change of slope of the tendon relative to the centroidal axis of the concrete. In the first diagram, the centroidal axis is constant and the tendon eccentricity changes. In the second diagram, the tendon is perfectly straight with no angle changes, but the concrete centroidal axis changes slope. Assuming the relative slopes between the tendon and the concrete are the same in both cases and the prestressing force is the same, both will result in exactly the same Mp diagram and exactly the same Equivalent uplift force at midspan.

Its effect is a moment diagram equal to P.e at any location along the tendon. For nice simple tendon profile eccentricities from the concrete centroid where the profile eccentricity matches the BM diagram of a load type, this can be represented by an "Equivalent Balanced Load". All this Equivalent Balanced Load does for you is give you an easy way to calculate P.e at each point. Yes, it creates stresses that negate the effect of an equal and opposite applied load to the structure, simply leaving you with an axial compression stress condition under that loading, but that is because the P.e created = -Mapp.

But the concept of Equivalent balanced Load" does not extend beyond that. It is an easy way to visualise the Pe effect of the tendon relative to loads, or to calculate a tendon profile to match a load condition.

The 3rd diagram takes this one step further with a harped tendon in a cranked beam. The stress condition in this beam is pure axial compression. There is no eccentricity even though the tendon profile is Harped. The centroid is also, so they negate each other.

This logic is described in good PT books. Possibly no modern books, but the real ones e.g. Guyon's Limit State Design of Prestressed Concrete, Leonhardt's Prestressed Concrete Design and Construction, TY Lin's Prestressed Concrete plus many others including some modern ones. Also a lot of courses on PT will cover it.

 

[KootK]

Strictly speaking, Australia is a continent, not a sub-continent.

Granted. However, I was really jonesing for McMahstas as the acronym. So bad ass.

Not due to any other forces induced in the tendon due to applied loads causing member curvature and increases in tendon force!

Well, yeah. Since the top, I've limited my scope to non-bonded PT.

And not looking at section capacity or member capacities

I'm happy to look at capacities and have not excluded them from my scope. My derivation above focused on using balanced load effects to calculate ultimate flexural capacity.

That is because the equivalent load is NOT simply caused by the change in slope of the tendon.

While I disagree with your conclusion here, know that I found your three examples very enlightening. I'll tackle them one at a time.

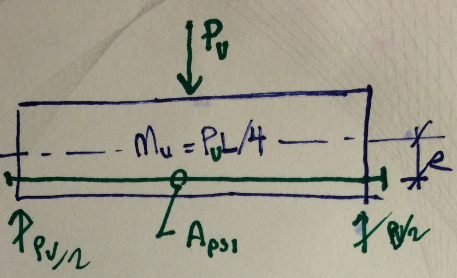
#3) This is an extremely salient example for demonstrating the internally equilibrated system that forms between the tendon and the concrete. The tendon does create a balancing load effect but that effect is perfectly offset by the P-delta action of the anchorage forces.

#1) I now see that this example is virtually identical to #3 in all of the ways that matter with respect to the balancing load effect. It could essentially be thought of as example #3 with some extra concrete thrown in. The balanced load effect is the same as it is for #3. The P-delta action of the anchorage forces is the same as it is for #3.

#2 This one caused me some heart palpitations for a while. That was until I realized that this one is not an example of balancing load effects. I feel that it fails to meet the fundamental criteria necessary to qualify as balancing load effect:

a) The effect is not generated by tendon curvature.
b) Forces transverse to the member's longitudinal axis are not generated.
c) Load is not "deposited" by the tendons at the supports.

Scenario two is no more an example of balanced load effects than is the beam shown below. In both instances, anchorage force eccentricity results in upwards curvature. However, in neither case is that exemplary of the load balancing effect phenomenon.

But the concept of Equivalent balanced Load" does not extend beyond that. It is an easy way to visualise the Pe effect of the tendon relative to loads, or to calculate a tendon profile to match a load condition.

Based on the examination presented above, I am still not convinced of this. I previously proved that balancing loads could be used to calculate ultimate capacities for the very simple case of a simply supported member. My strong suspicion is that, with appropriate modification to the technique, balancing loads could be used to determine the ultimate capacity of a system of any complexity.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[rapt]

Kootk,

1 Unbonded prestress does increase in stress under ultimate conditions. If you understood anything about PT design you would understand that. Under curvature of the member, the tendon elongates thus increasing the tension in the tendon. It is just not related to the concrete strain at any point in the member, it is related to the overall member length change at the depth of the tendon. That is why I had to qualify it.

2 1 above does not have any Pdelta effect as you call it. How can it be the same as for 3.

3 Balanced load effect is just one way of calculating Pe. Both 1 and 2 have the same Pe. They both generate the same Equivalent Balanced Load. Balanced load is related to the eccentricity of the tendon from the concrete centroid. Not just the tendon curvature. The tendon in 2 does have a change in curvature relative to the concrete centroid. It produces an Equivalent Balanced Load, exactly the same as the Equivalent balanced Load in 1.

4 You cannot predict ultimate capacity using balanced loads!

 

[KootK]

Unbonded prestress does increase in stress under ultimate conditions.

Not very much it doesn't. So little, in fact, that we don't bother to account for it in our procedure for calculating ultimate moment capacity.

If you understood anything about PT design you would understand that.

Ah yes... there's that delightful bedside manner again.

1 above does not have any Pdelta effect as you call it. How can it be the same as for 3.

Number one does have the P-delta effect. You just have to recognize that it's about the tendon, not the concrete. See details A&B of my little "proof", repeated below (second batch of sketches).

3Both 1 and 2 have the same Pe. They both generate the same Equivalent Balanced Load. Balanced load is related to the eccentricity of the tendon from the concrete centroid. Not just the tendon curvature. The tendon in 2 does have a change in curvature relative to the concrete centroid. It produces an Equivalent Balanced Load, exactly the same as the Equivalent balanced Load in 1.

Would you call the beam shown in the first sketch below (prismatic/flat tendon) an example of balancing load? I doubt it. If not, how do you distinguish between that scenario and your scenario #2? To me, they both just look like beams acted upon by an eccentric, axial, anchorage force. And that's not balancing load.

4 You cannot predict ultimate capacity using balanced loads!

Except that I already did. Algebraically no less. See my derivation, repeated below (third batch of sketches). As yet, no one's refuted it in any way.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

@Doug: I wanted to come back to the GGB/SH stuff as you've made some interesting observations there. Keep in mind that I've only got a KootK mental construct of what you've described. It may not be entirely accurate.

1. In both the bending moment in the concrete is the same at every section (zero).

This is definitely true for GGB. I find it murky for SH. SH has no concrete stress other than the arch compression. But then the arch compression could be construed as a flexural stress in the sense that it is a compression field eccentric to the centroid of the member.

2. The axial force in the concrete is constant in the GGB system and varying from zero at the ends to same as GGB at mid-span in the SHB system.

Agreed for GGB. Not so sure for SH. As a tied arch, I would think that SH would still have a substantial axial force where the arch meets the tie.

3. In the GGB the shear forces are carried entirely through the tendons, but in the SHB the shear forces are carried entirely through the concrete (in arching, rather than through shear deformation).

Agreed

4. An important point (I think) is that you can only balance one load, but at this load the two structures are both acting as balanced load mechanisms. The only difference is that in the GGB the shear forces are carried by catenary action in the steel, and in the SHB the shear is carried by arching in the concrete.

Agreed. You can only balance one load perfectly. For all other loads, you'd be under-balanced, over-balanced, and/or differently balanced.

5. For any increased load the moment is carried entirely by bending stresses in the concrete in a draped debonded system (because the tendon force does not increase), or jointly by the concrete and increased force in the tendons in a bonded system. In both cases the increased shear is carried through the concrete.

Agreed.

If I understand correctly, the ultimate capacity of both GGB and SH could be conceived as:

1) Balanced load contribution from catenary/arch up to balanced load plus;
2) Flexural contribution of section beyond balanced load.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[hokie66]

This is all a bit over my head, but just wanted to point out one thing. Don't know whether it changes your argument or not, but the Sydney Harbour Bridge is a thrust arch, not tied.

 

[IDS]

Hokie/KootK - probably the Sydney Harbour Bridge wasn't that great a choice for the analogy, but the thinking was:

- Start with something where the roadway is vertically connected to a member that transfers the load to the support, but with the load transfer member for the SHB working in compression rather than the tension in the cables of the GGB.

- Transfer the external anchorage to an anchorage into the deck, so in the same way that the GGB was converted into a post-tensioned beam, with the anchor load carried by the concrete in uniform compression, the idea was that the compressive external restraint force at the ends of the actual bridge would be converted to a horizontal tie force in the prestress strands.

The problem is that to get the balanced load mechanism to work with uniform compression in the concrete the prestress force has to be continuously varying from a maximum at mid-span to zero at the support (so varying the force rather than the eccentricity), so whereas we could convert the GGB into a post-tensioned beam quite neatly, it doesn't really work with the SHB.

But really the point was: if we look at load balancing as the moment generated by an eccentric horizontal force balancing the moment due to the vertical gravity force, then we can have either a constant force with varying eccentricity, or a varying force with constant eccentricity, or anything in between.

A couple of other points:

Regarding the force in the draped tendon when the load was increased from the balance load to the ultimate load, I suggested that in the debonded case the force would remain constant, on the basis that it was anchored at the concrete centroid. In fact the cable will pass entirely through zones where the concrete strain due to the increased load is tensile, so there will be increased tensile strain in the tendon, especially after cracking of the concrete, but this strain will be distributed uniformly along the tendon, so the increase in strain at mid-span will be much less than for the bonded case. (Also there will be some position of the anchorages, above the neutral axis, where there will be no increase in length of the cable due to the increased load).

Regarding calculation of the ultimate moment including the load-balancing moment, I agree that you could add the load-balancing moment, and the moment about the concrete centroid due to concrete stresses and increase in tendon stresses. In effect you would be just subtracting the moment due to tendon eccentricity, then adding it back in again, as the balanced load moment.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[rapt]

Hokie,

Don't worry, the Golden Gate Bridge is a pure suspension bridge with all loads transferred from the deck by hangers to the tension cables acting in catenary action over the towers to the anchor points well back from the towers. The only compression members are the Towers, and they are vertical! As it is designed and built, it acts nothing like a flexural beam with unbonded tendons.