Agent666
Structural
- Jul 2, 2008
- 3,080
Hi All
Couple of questions about how people deal with the EC2 parabolic-rectangular (or any other non rectangular) compression block in practice/practical design, especially when dealing with non-rectangular sections or bi-axial bending where the width of the block is changing with respect to depth from the extreme compression fibre:-
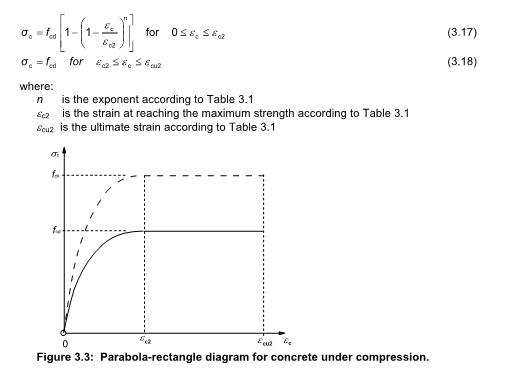
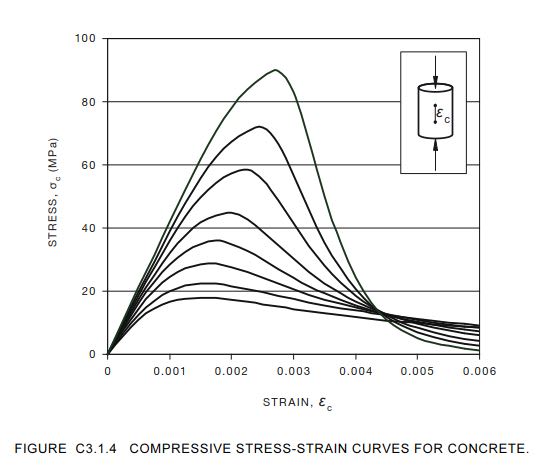
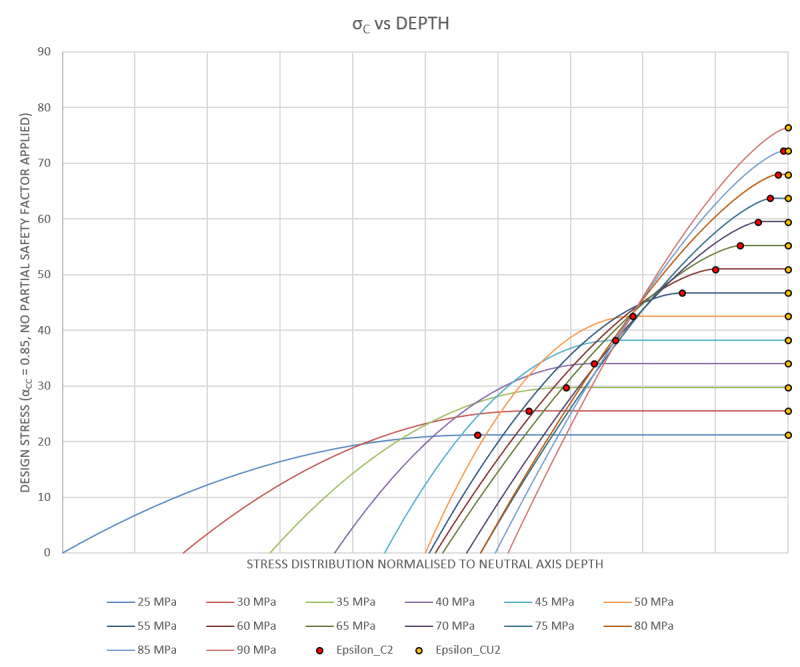
For a rectangular section (i.e. beam) with flexure about one axes only, its quite easy to resolve the parabolic distribution to an equivalent rectangular stress block for the purposes of calculating the ultimate capacity of a section, i.e. same area and centroid via integrating appropriately the 3.17 equation in EC2.
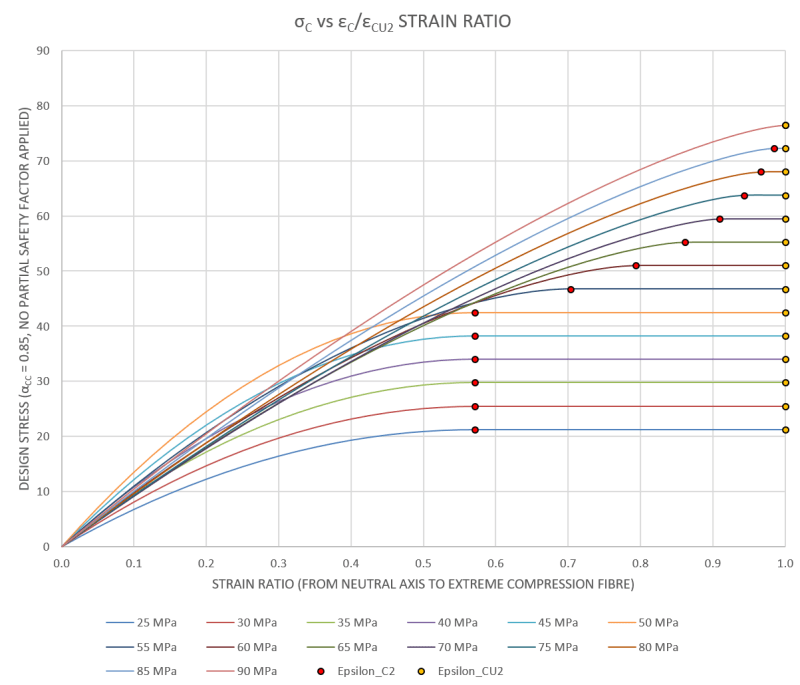
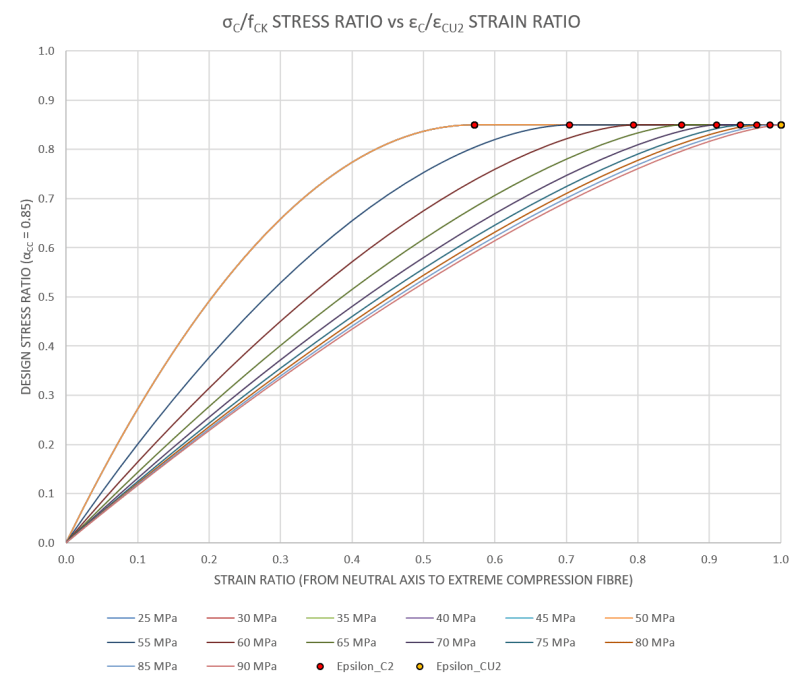
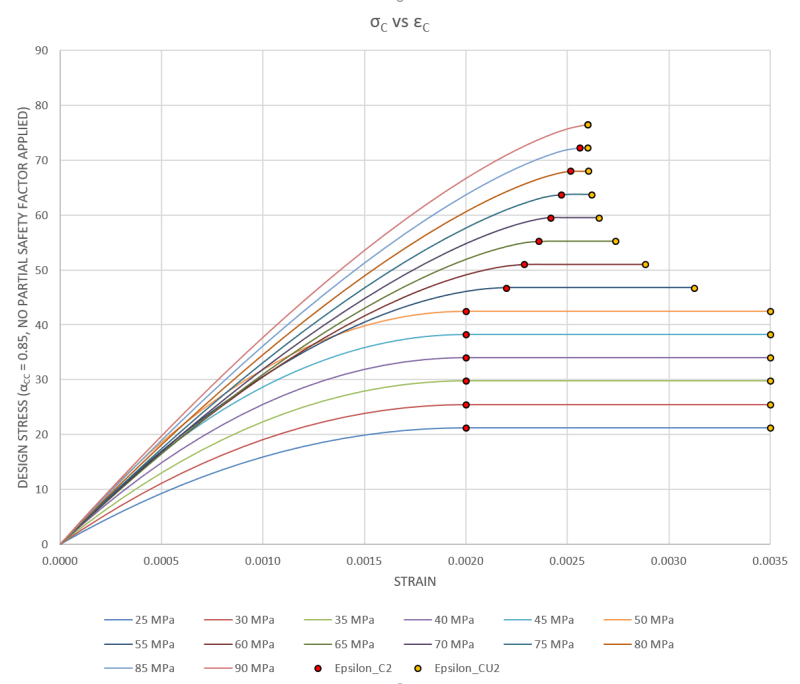
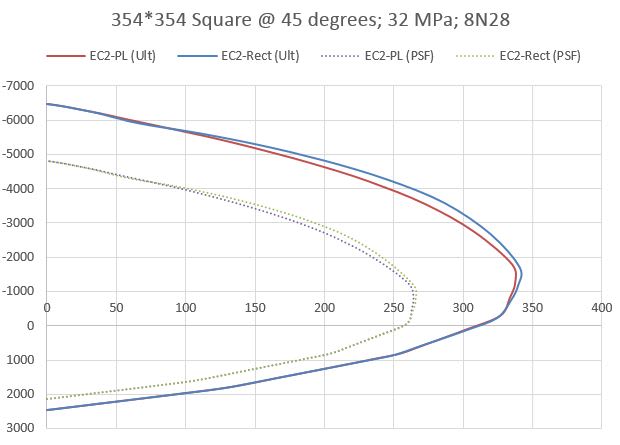
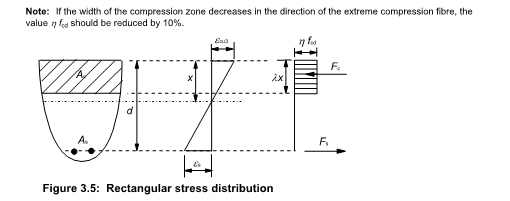
This only works for rectangular sections with one principle axes moment. For anything non rectangular (say a circular section), or bi-axial bending in a rectangular section (i.e. column), do people typically just use the rectangular stress block from EC2 and apply the 10% reduction to η (the reduction in f_ck) noted in clause 3.1.7(3) and not 'go there' with the parabolic curve as it all gets too hard.
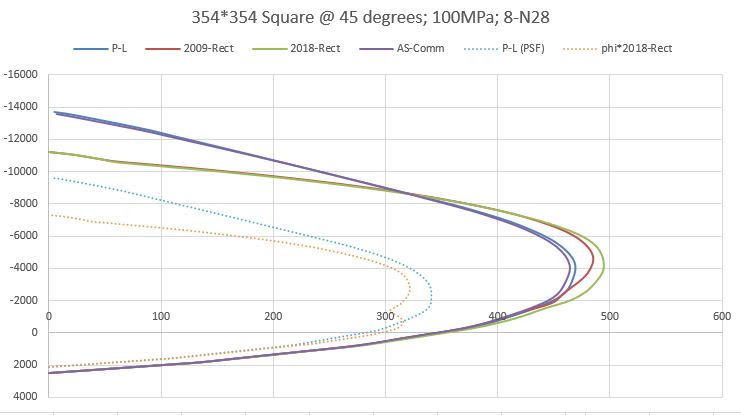
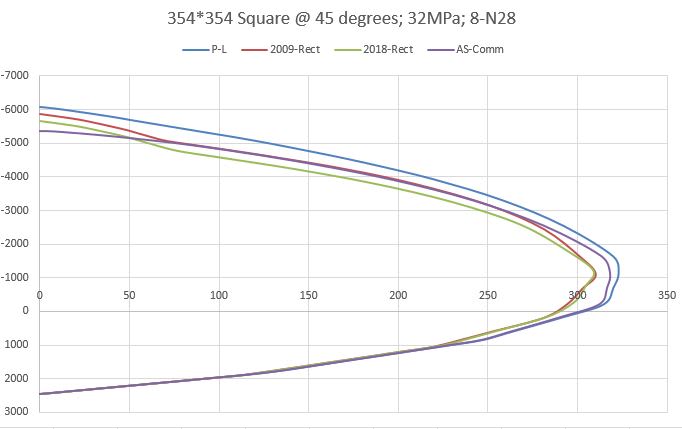
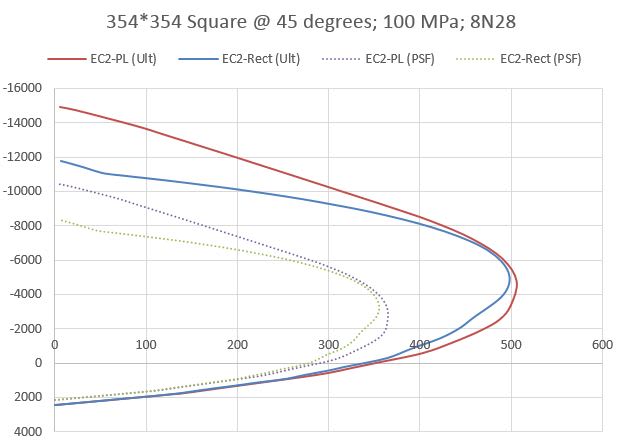
If doing things by hand I'd simply do it this way as its close enough for ultimate capacity, but for spreadsheets you can obviously go to the effort of working things out using the parabolic or bi-linear relationship and apply the EC2 parabolic distribution to the non-rectangular section and work out the area and centroid (presumably need to integrate the 3.17 relationship over the curve and the section shape (i.e. find the volume and centroid of the resulting 3D stress block in the section).
I can't imagine this is too hard, though my integrating skills were put to the test just doing the 2D problem for a rectangular section, and have never attempted finding the centroid and volume of a 3D shape like this!
So how do people deal with this in practice, we are told these more advanced curves are better/more accurate, etc, etc... but is it all just too hard to do in practical design unless you are using some software that already does these things for you?
Also is anyone aware of any generalised solutions for the volume and centroid of the parabolic-rectangular stress block for 1) circular or 2) rectangular sections with biaxial actions?
Couple of questions about how people deal with the EC2 parabolic-rectangular (or any other non rectangular) compression block in practice/practical design, especially when dealing with non-rectangular sections or bi-axial bending where the width of the block is changing with respect to depth from the extreme compression fibre:-

For a rectangular section (i.e. beam) with flexure about one axes only, its quite easy to resolve the parabolic distribution to an equivalent rectangular stress block for the purposes of calculating the ultimate capacity of a section, i.e. same area and centroid via integrating appropriately the 3.17 equation in EC2.
This only works for rectangular sections with one principle axes moment. For anything non rectangular (say a circular section), or bi-axial bending in a rectangular section (i.e. column), do people typically just use the rectangular stress block from EC2 and apply the 10% reduction to η (the reduction in f_ck) noted in clause 3.1.7(3) and not 'go there' with the parabolic curve as it all gets too hard.

If doing things by hand I'd simply do it this way as its close enough for ultimate capacity, but for spreadsheets you can obviously go to the effort of working things out using the parabolic or bi-linear relationship and apply the EC2 parabolic distribution to the non-rectangular section and work out the area and centroid (presumably need to integrate the 3.17 relationship over the curve and the section shape (i.e. find the volume and centroid of the resulting 3D stress block in the section).
I can't imagine this is too hard, though my integrating skills were put to the test just doing the 2D problem for a rectangular section, and have never attempted finding the centroid and volume of a 3D shape like this!
So how do people deal with this in practice, we are told these more advanced curves are better/more accurate, etc, etc... but is it all just too hard to do in practical design unless you are using some software that already does these things for you?
Also is anyone aware of any generalised solutions for the volume and centroid of the parabolic-rectangular stress block for 1) circular or 2) rectangular sections with biaxial actions?