Modern Steel Construction Steel Quiz 12

[SteelPE]

I was looking at the steel quiz in the 10/17 issue of MSC. I was able to pick up the problem quickly as I'm sure others have. However, I had a slightly different answer, I came to the conclusions that the framing plan shown had beams that required themselves for support and therefore would not work. However the article simply states that the configuration is difficult to erect. Is the framing plan shown even structurally stable utilizing simple structural theory?

 

[atrizzy]

The ninja bomb has something to do with it, I think...
It's just that instead of an external load the applied loads are all internal (between one member and another) and the friction force holds them together. Your throwing it at your brother's head would be analogous to knocking one of the reciprocal members off of another with a lateral force.

 

[chicopee]

I am not a structural guy, however, I can visualize a catastrophic failure of a roof with that system similar to the catastrophe of the Hartford civic center space frame roof.

 

[Huevo]

Just business as usual with an indeterminate structure organizing itself to resist load.

Assuming small deflections, I would not say that it is indeterminate but rather quite determinate.

 

[BAretired]

I believe that the structure is statically determinate, contrary to some of the comments above. If plan dimensions are provided, all reactions can be obtained by statics alone. An iterative process is unnecessary to solve the problem.

BA

 

[KootK]

Assuming small deflections, I would not say that it is indeterminate but rather quite determinate.

Huh. It seems that the reciprocal framing plot just won't stop thickening. Like delicious Thanksgiving gravy.

I disagree and believe that the system is indeterminate and that the reactions can only be found by equilibrium when you have symmetry in play. Here's my reasoning by way of thought experiment:

As I mentioned above a few times now, this system has the characteristic of being quite similar to two moment spliced, orthogonal crossing beams. Hopefully that is not in dispute. And, just like two crossing beams, the loads distribute based on relative stiffness.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

I disagree. The reactions are not related to stiffness. The problem is determinate.

For example, suppose each beam is 10' long and the square opening in the middle is 5'x5' such that each beam is supported at one end by an external support and at the other end by another beam. In all cases, the reaction occurs at midpoint of the supporting beam.

If all beams are loaded with uniform load W then the total load on the grid is 4W. Each of the four reactions is W due to symmetry.

Assume that only Beam B1 carries uniform load W. The others are not loaded. Beam B1 bears on B2 which bears on B3 which bears on B4 which bears on B1. The reaction of B4 on B1 is P. B1 reaction is W/2 + P/2 which falls at the midpoint of B2. B2 exerts a reaction of W/4 + P/4 on B3 which in turn dumps W/8 + P/8 on B4.

B4 reacts with W/16 + P/16 on B1, but we called that P, so:
P = W/16 + P/16
Solving, P = W/15 and the reaction of B1 can be found to be R = 8W/15
The remaining three reactions are 4W/15, 2W/15, and W/15 for B2 to B4 respectively.
The sum of all reactions is W as expected.


BA

 

[KootK]

Each of the four reactions is W due to symmetry.

Right. But does this not invalidate your example since the symmetric situation is the one unique case where equilibrium alone can yield a solution?

Take your geometrically symmetric example and run these two thought experiments on it:

1) All members W21.

2) The North-South members Wx21; the East-West members 2X4 SPF.

Think the four reactions are still W for both cases? I don't. And that implies indeterminacy.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

Just realized that your example is two seperate examples, one symmetrically loaded and one not. I'll have to leave that for another day. It's a bit of a mouthful for digesting tonight.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

Yes KootK, there are two examples, one with all beams loaded, the other with only one beam loaded.

If the problem is statically determinate, the reactions must be the same even if the beam size is variable. If a 2x4 SPF is capable of carrying the load, then the external reactions must be equal with all beams equally loaded.

BA

 

[KootK]

If the problem is statically determinate, the reactions must be the same even if the beam size is variable.

Right, but my contention is that the problem is not statically determinate.

If a 2x4 SPF is capable of carrying the load, then the external reactions must be equal with all beams equally loaded.

Is the distribution below not valid with unequal reactions and symmetric loading?

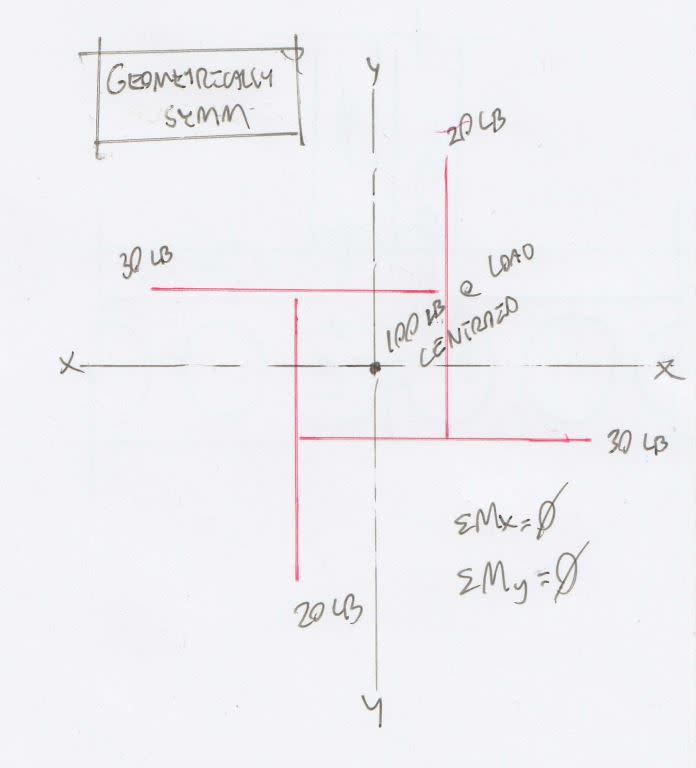
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

In your latest example, the external equilibrium is satisfied but you have not specified how the 100# load gets into the system. If the load is applied uniformly on each beam, i.e. 25# each, I believe the external reactions will be equal by statics. If the load is applied unsymmetrically, say 50# each to B1 and B3 and zero load to B2 and B4, I'm not so sure the external reactions would be equal. It could be determined by statics but my poor old brain doesn't feel like tackling that problem right now.

To take your example a bit further, you could have external reactions of 50# and 0# instead of 30# and 20# which would still satisfy external equilibrium.

BA

 

[BAretired]

Beams have been numbered B1 through B4 in the attached sketch. As noted, the only applied load is W on B1 which is assumed to occur at 0.75L from the left end where L is the beam length. The external reactions are labeled R1, R2, R3 and R4 which apply to B1 through B4 respectively. The reaction of B1 to B2 is assumed to be P which is to be determined by statics.

Beams B2, B3, and B4 have a beam reaction applied at midspan from B1, B2 and B3 respectively. Consequently, their reaction at each end is half of that load.

All beams are simple spans, so the calculation is relatively simple.
It was found that for load W at the location shown:
R1 = 0.3W
R2 = 0.4W
R3 = 0.2W
R4 = 0.1W

R1 + R2 +R3 +R4 = W as expected.

If all four beams have a load W acting at 0.75L from the external end, the principle of superposition can be used to find that each external reaction is equal to W.

BA

 

[BAretired]

If load W is placed only on B1 and B3 at 0.75L from the end, using superposition, reactions are R1+R3 or R2+R4 which means they are all equal, namely W/2. The sum of all four external reactions is 2W as expected.

BA

 

[KootK]

I am finding your argument pretty persuasive BA. And you definitely get an A+ for effort. Although I do think it cruel of you to use my own sketches to dismantle my theories. You're retired... you shouldn't even have Bluebeam damn it!

I think DETstr should step up and adjust her RISA model to run a test case of my specification:

- All members 10'
- Oculus N-S dim 2'
- Oculus E-W dim 4'
- Load applied at one of the oculus corner connections
- Case I: all members W8x21
- Case II: the N-S members switched to 2x4 SPF

How about it DETstu? I don't normally attempt to assign others homework but I'm not yet a RISA jockey and I'm so damn busy that I'm working at 9:30 pm on a Wednesday... There's a big, shinny magenta star in it for you?





I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[Huevo]

As I mentioned above a few times now, this system has the characteristic of being quite similar to two moment spliced, orthogonal crossing beams. Hopefully that is not in dispute. And, just like two crossing beams, the loads distribute based on relative stiffness.

This is very much in dispute for me at least.

I don't agree that the orthogonal crossing beams with moment connections behaves at all similar to the reciprocal frame.

FWIW I also strongly believe that the timber moment splice posted above is also determinate.

The key to determinacy was if the member forces could be obtained without the use of a stiffness function. Symmetrical or not, the member forces can be found without the use of a stiffness function for the reciprocal frame in this discussion. This of course assumes that you also base your argument on there being small deflections and boundary conditions that prevent dubious tension ring and catenary behavior.

 

[KootK]

I don't agree that the orthogonal crossing beams with moment connections behaves at all similar to the reciprocal frame.

Really, not at all? You place a load among some members, none of which extends the full distance between supports. And somehow, like magic, that load is transferred out to the supports. That doesn't sound anything like splicing to you?

FWIW I also strongly believe that the timber moment splice posted above is also determinate.

I never suggested otherwise so we're in agreement there.

Symmetrical or not, the member forces can be found without the use of a stiffness function for the reciprocal frame in this discussion.

Can they? That really is the question. And perhaps they can. As I mentioned earlier, I'm coming around to BA's reasoning. That said, one must recognize the important logical distinction between being able to generate a solution (one of many perhaps) and being able to generate the solution (unique). BA's adroitly demonstrated that (a) solution can be found without invoking stiffness. In my mind,however, it has not yet been demonstrated that he has found a unique solution. And that's whole thing with indeterminate structures after all. There are infinite solutions that satisfy equilibrium when that is the only criterion applied. That's why I posted my latest sketch showing the statically admissible unequal reactions: to highlight that it's not enough just to find one solution; we need to also exclude all of the others.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[nonplussed]

Not sure if this counts as a reciprocal frame or not but here's a cool stair I saw while in Europe.

 

[TehMightyEngineer]

Not reciprocal as the last beam in the spiral doesn't load up the first. Very cool framing though.

Professional Engineer (ME, NH, MA) Structural Engineer (IL)
American Concrete Industries

https://www.facebook.com/AmericanConcrete/

 

[KootK]

So I decided to do my own modelling. The RISA file is attached for anyone who would like to critique it.

- At run time, I get a program complaint of "Z reactions do not sum to match Z loads". I'd be curious to know if anyone can resolve that as, to some degree, it casts a bit of doubt on the solutions.

- Presumably, because of the runtime error just mentioned, I'm unable to report joint reactions. They can be gotten indirectly via shear diagrams.

- I believe that this test supports the hypothesis that these are statically determinate systems. The response parameters, such as the moments shown below, do shift slightly from one model to the next. However, that's a very slight shift over what is about a 100 fold increase in vertical displacement.

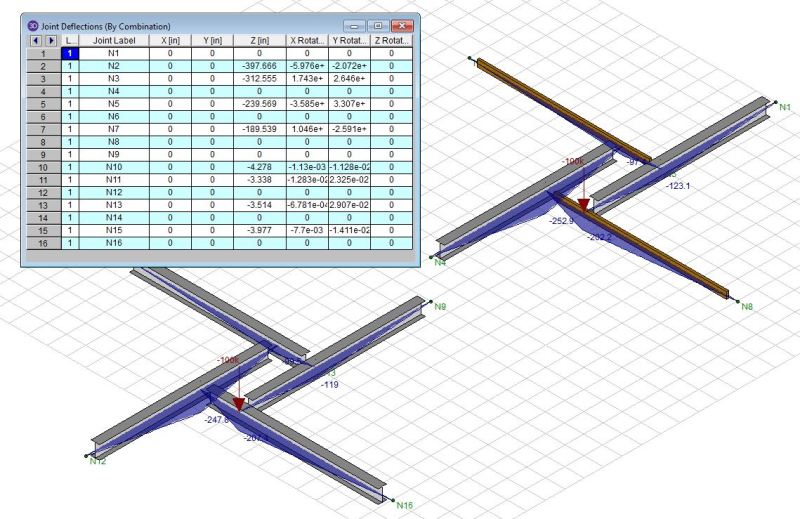
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

The model's picking up some undesired torsion, particularly the wood version. Anybody know a simple solution to that? Updated model attached.

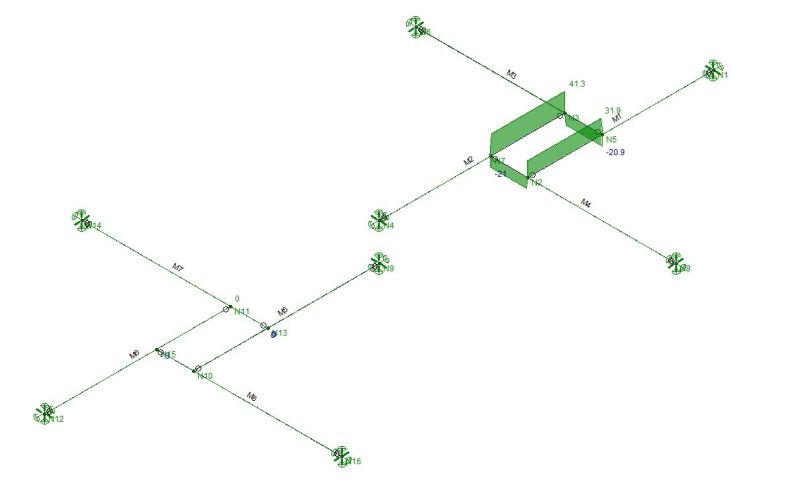
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.