Multiple single segment with dynamic modifier

[Wuzhee]

Hello,

This probably has been discussed before, but what's the difference between the two callouts below?

!EDIT! : profile applies between A <-> B. Forgot to add that under fcf.
MSS without datums

MSS with dynamic, w/o datums.

 

[3DDave]

Scaling was considered and rejected for what appears to be excellent reasons.

An S curve cannot have a dynamic tolerance zone? I missed where it says that. If the curve in figure 11-38 was an S curve then it could not have a dynamic tolerance even though the axis remains constant? A constant location? It does have a reversal.

It's also a bit weird to claim that constant location is required when there are examples that clearly show the zone shifted and rotated. The proportions of the closed shape are definitely not kept.

 

[Burunduk]

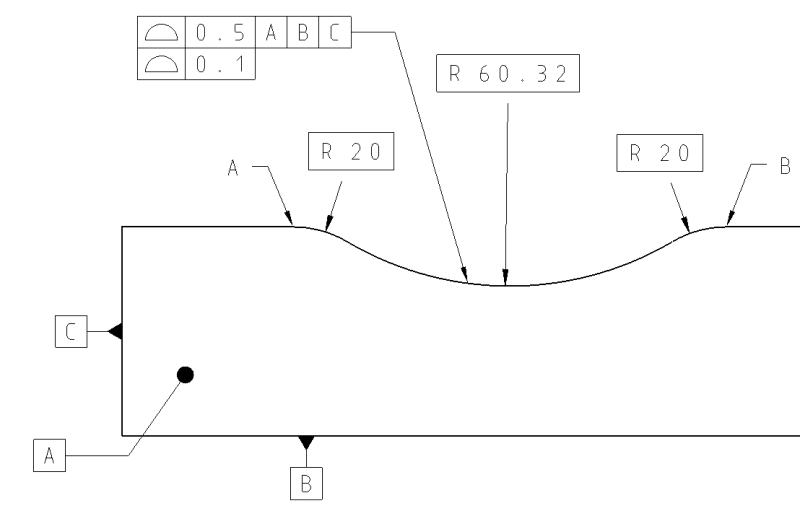
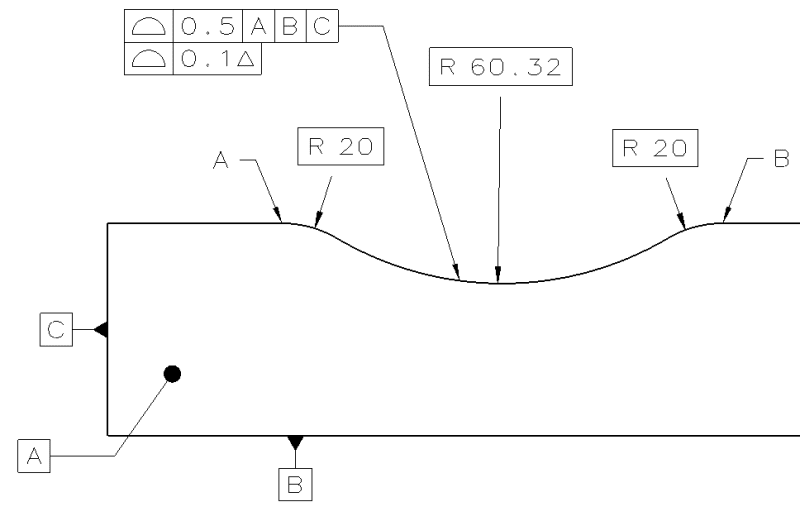
Constant location is in the context of the multiple single segment profile with the bottom segment being the dynamic profile, with datum references, used as a refinement of form, location and orientation.
Figure 11-37 represents what happens to a closed shape tolerance zone in such a case. All the conditions given in 11.10.3 are met. The location of the tolerance zone in the A, B DRF doesn't change by the process in which the tolerance zone progresses from the true profile (expands or contracts). It would not be so if the tolerance was applied only to the bottom or top arc instead of all-around.

11–38 shows a surface of revolution, so regardless of its exact shape,'S' or not, it doesn't suffer from the contradiction between constant location and the tolerance zone being allowed to offset. I described that contradiction for open shapes ('S' included). This contradiction is most obvious for a planar tolerance zone.