Eng-Tips is the largest engineering community on the Internet
Intelligent Work Forums for Engineering Professionals
-
Congratulations waross on being selected by the Tek-Tips community for having the most helpful posts in the forums last week. Way to Go!
Multiple single segment with dynamic modifier
- Thread starter Wuzhee
- Start date
You failed to expand anything. Anyway I'm not the one who fails to see that coincidence doesn't mean equivalence. There is multiplication without addition.
2 meters + 2 meters + 2 meters is 6 meters, while 2 meters time 3 meters is 6 square meters.
Did your college forget to mention that units matter? Any class on dimensional analysis (hint - it's not Geee Deee and Teee)
2 meters + 2 meters + 2 meters is 6 meters, while 2 meters time 3 meters is 6 square meters.
Did your college forget to mention that units matter? Any class on dimensional analysis (hint - it's not Geee Deee and Teee)
3DDave said:
Or 6 meters. Depends on whether the calculation is for length or area.
6 meters is more related to the topic being discussed - a special case for which 2 types of transformation are equivalent, like 2 times 3 and 2 added 3 times.
But why do I still expect you to understand a context?
"If it was length, one would be a scalar without units"
That's true, and that is added to a series of your recent phenomenal displays of incomparable mathematical expertise.
I only wonder why you haven't pointed out the specific mathematical difference between translation and progression for the special case of a plane, which is now the topic. I expected you to describe that difference in terms of vectors' directions and magnitudes.
That's true, and that is added to a series of your recent phenomenal displays of incomparable mathematical expertise.
I only wonder why you haven't pointed out the specific mathematical difference between translation and progression for the special case of a plane, which is now the topic. I expected you to describe that difference in terms of vectors' directions and magnitudes.
"Nothing translates."
Sorry, this one is a bit less impressive (I hope greenini approves this wording).
If the transformation moved all points of the planes of the tolerance zone the same distance and in the same direction in a coordinate space, this is translation. You can call it other names if it suits additional definitions, but nevertheless it conforms to the definition of translation. So if translation is constrained, the operation is invalid.
What matters is not the name you choose to call it, but what it is mathematically.
Sorry, this one is a bit less impressive (I hope greenini approves this wording).
If the transformation moved all points of the planes of the tolerance zone the same distance and in the same direction in a coordinate space, this is translation. You can call it other names if it suits additional definitions, but nevertheless it conforms to the definition of translation. So if translation is constrained, the operation is invalid.
What matters is not the name you choose to call it, but what it is mathematically.
- Thread starter
- #88
![[roll1]](/data/assets/smilies/roll1.gif "[roll1] [roll1]")
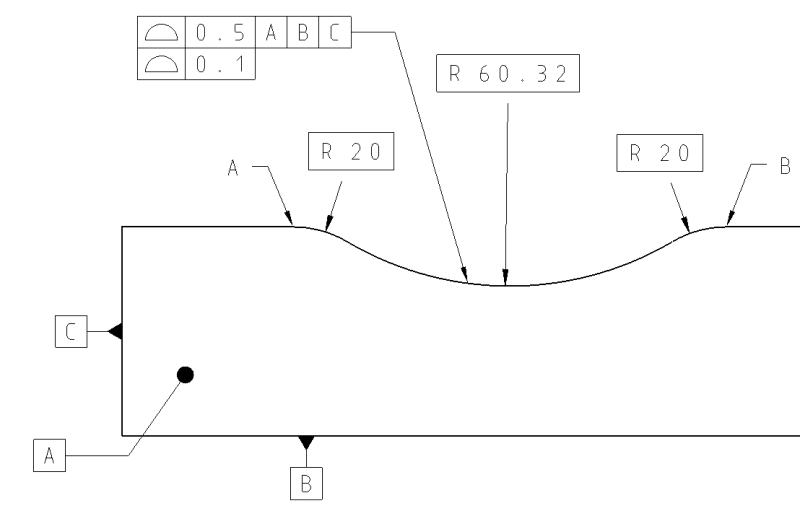
So, in figure 11-37 the sides translate and the arcs progress?
Or do all surfaces progress?
Or do the arcs translate and scale?
Which of these is supported by the description?
"When the dynamic profile tolerance modifier is applied, the zone is permitted to progress (expand or contract normal to the true profile) while maintaining the specified constant width (distance between the boundaries)."
Is there the word "translate" or "scale" in that sentence?
One must eliminate any interpretation using the word translate.
Or do all surfaces progress?
Or do the arcs translate and scale?
Which of these is supported by the description?
"When the dynamic profile tolerance modifier is applied, the zone is permitted to progress (expand or contract normal to the true profile) while maintaining the specified constant width (distance between the boundaries)."
Is there the word "translate" or "scale" in that sentence?
One must eliminate any interpretation using the word translate.
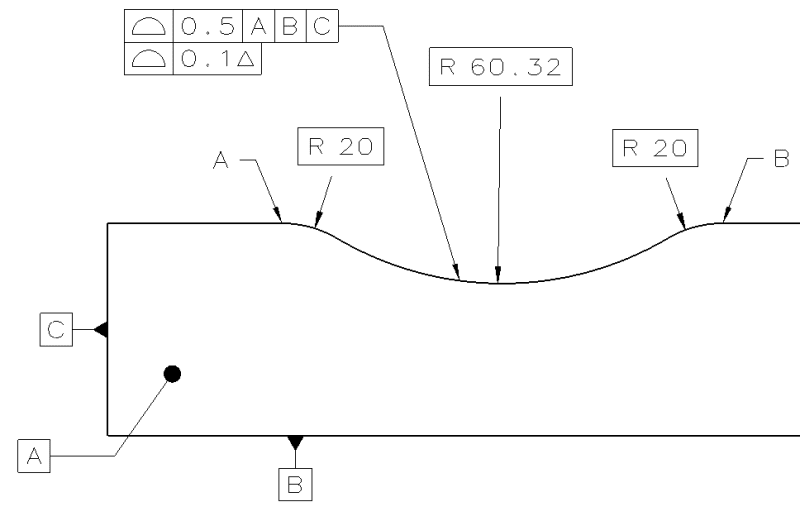
The entire opening is toleranced by profile in each segment, and the entire all-around tolerance zone is treated as a whole and not dissected to portions. The dynamic profile tolerance zone is allowed to progress but not translate, which means it is scaled without changing the original shape and proportions. The location of the complete tolerance zone relative to the DRF doesn't change in the process.3DDave said:
Progressing isn't scaling and scaling isn't a uniform operation. I missed where the phrase "as a whole" appears.
Are you proposing 3 rules:
1) If it is planar then only translation
2) if it is closed then it is scaling
3) if it is open, but not planar, then it's offset
Except the figures rule out #2 as the correct interpretation and #1 is an incorrect understanding that happens to look like #3.
Since it happens as a group then are the flats translated or are the scaled or are they offset or is there some other term you would like to add?
Are you proposing 3 rules:
1) If it is planar then only translation
2) if it is closed then it is scaling
3) if it is open, but not planar, then it's offset
Except the figures rule out #2 as the correct interpretation and #1 is an incorrect understanding that happens to look like #3.
Since it happens as a group then are the flats translated or are the scaled or are they offset or is there some other term you would like to add?
For what it's worth, this is how ISO explains the concept in their 1101:2017. They call it Offset Zone (OZ). No closed contour is needed to explain it. The constraints of the tolerance zone are explained as
a relation of the tolerance zone to the theoretically exact feature (TEF). The presence or absence of datum feature references in the OZ profile callout affects the constraints of the TEF.
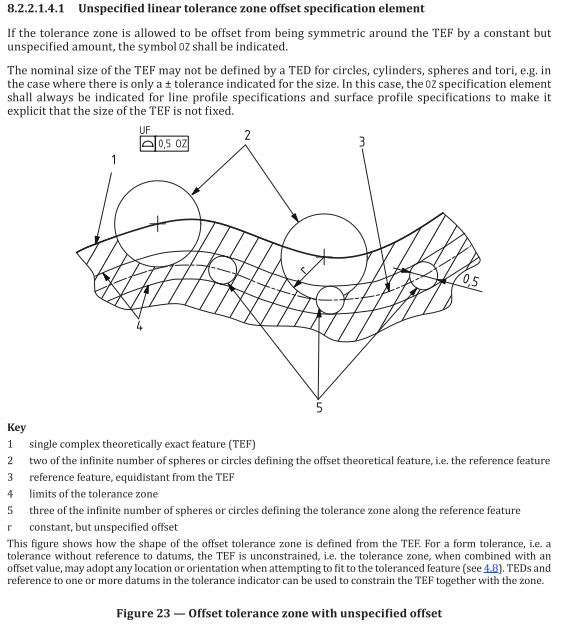
a relation of the tolerance zone to the theoretically exact feature (TEF). The presence or absence of datum feature references in the OZ profile callout affects the constraints of the TEF.
Scaling can be uniform or non-uniform and obviously in the context of progression per the dynamic modifier I meant uniform scaling, i.e. change of size with constant proportions of the shape (as I mentioned).3DDave said:
Is it new to you that each tolerance zone is a separate, complete entity that is not disassembled to elements?3DDave said:
Burunduk and 3DDave,
Dynamic profile was originally described in terms of scaling the tolerance zone (in early drafts). Then it was determined that this wasn't quite the mechanism that was needed. One disadvantage was that scaling requires a well-defined point to scale relative to, and the "center" point is only well-defined on simple (i.e. symmetric) closed shapes. Another disadvantage was that when scaled, the tolerance zone doesn't keep a consistent thickness unless the true profile is a simple (i.e. symmetric) shape. It was decided that progression was a better mechanism - it isn't ideal in every way, but it is consistent with other things in Y14.5. Runout zones don't scale - they progress (because the FIM concept is equivalent to the zone progressing). Also, unequally disposed and unilateral profile zones are progressed and not scaled. With progression, dynamic profile is quite easy to add to the existing profile definitions (the constraint-based ones, anyway). If it was scaling, this would be very difficult. We made sure that they defined it in a way that would be clear and straightforward to mathematize ;^).
Thanks to pmarc for posting the ISO 1101 offset zone definition - it's basically (pardon the pun) the same thing as dynamic profile, just defined with different terminology and an additional sphere to represent the offset.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Dynamic profile was originally described in terms of scaling the tolerance zone (in early drafts). Then it was determined that this wasn't quite the mechanism that was needed. One disadvantage was that scaling requires a well-defined point to scale relative to, and the "center" point is only well-defined on simple (i.e. symmetric) closed shapes. Another disadvantage was that when scaled, the tolerance zone doesn't keep a consistent thickness unless the true profile is a simple (i.e. symmetric) shape. It was decided that progression was a better mechanism - it isn't ideal in every way, but it is consistent with other things in Y14.5. Runout zones don't scale - they progress (because the FIM concept is equivalent to the zone progressing). Also, unequally disposed and unilateral profile zones are progressed and not scaled. With progression, dynamic profile is quite easy to add to the existing profile definitions (the constraint-based ones, anyway). If it was scaling, this would be very difficult. We made sure that they defined it in a way that would be clear and straightforward to mathematize ;^).
Thanks to pmarc for posting the ISO 1101 offset zone definition - it's basically (pardon the pun) the same thing as dynamic profile, just defined with different terminology and an additional sphere to represent the offset.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
I'd prefer "uniform offset" vs "progression" as it matches the typical vocabulary.
Scaling is how mold-shrink works and isn't those.
Uniform offset is how profile of surface, profile of line, circularity, cylindricity, total runout, and circular runout, work. For a refinement of profile to work differently than profile does would be really odd.
In the production of parts except by casting (for which a separate document fails to deal with shrinkage if I recall correctly) tool wear and oversize tools produce offset errors, not isotropic scaling variation.
Scaling would typically be noted by a percent deviation from ideal with only one dimension controlling the acceptance for the entire feature.
Scaling is how mold-shrink works and isn't those.
Uniform offset is how profile of surface, profile of line, circularity, cylindricity, total runout, and circular runout, work. For a refinement of profile to work differently than profile does would be really odd.
In the production of parts except by casting (for which a separate document fails to deal with shrinkage if I recall correctly) tool wear and oversize tools produce offset errors, not isotropic scaling variation.
Scaling would typically be noted by a percent deviation from ideal with only one dimension controlling the acceptance for the entire feature.
3DDave,
I agree that the term "progression" isn't ideal - it could have been described as uniform offset.
There would be some applications for a scaling tolerance, and maybe this will be added to the standard sometime in the future (I don't know of any current plans). I agree that offset-related variation would be more commonly encountered in most design and manufacturing situations.
One of the things that resonated with me about dynamic profile was the connection to total runout. This isn't stated anywhere in the standard, but it's there. I would say that dynamic profile is sort of a generalization of total runout, or that total runout is a subset of dynamic profile ;^). It's the same type of zone, only dynamic profile is not restricted to surfaces of revolution with a datum axis. In theory, you could inspect dynamic profile as FIM of a dial indicator, if you had a way of sweeping the indicator along the true profile.
I remember that there was a difference of opinion in the committees on whether or not total runout could be applied to a cone or curved surface. They show circular runout on these shapes, but not total runout, and the text doesn't say one way or another. I never had a problem with it myself, but some people were concerned over situations where the "true profile" had directly toleranced dimensions (like the included angle on a conical feature). Now we don't have to worry about that anymore, and we can just leave the runout definitions the way they are. If we need a progressing/offsetting zone on a cone or curved surface, we can use dynamic profile.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
I agree that the term "progression" isn't ideal - it could have been described as uniform offset.
There would be some applications for a scaling tolerance, and maybe this will be added to the standard sometime in the future (I don't know of any current plans). I agree that offset-related variation would be more commonly encountered in most design and manufacturing situations.
One of the things that resonated with me about dynamic profile was the connection to total runout. This isn't stated anywhere in the standard, but it's there. I would say that dynamic profile is sort of a generalization of total runout, or that total runout is a subset of dynamic profile ;^). It's the same type of zone, only dynamic profile is not restricted to surfaces of revolution with a datum axis. In theory, you could inspect dynamic profile as FIM of a dial indicator, if you had a way of sweeping the indicator along the true profile.
I remember that there was a difference of opinion in the committees on whether or not total runout could be applied to a cone or curved surface. They show circular runout on these shapes, but not total runout, and the text doesn't say one way or another. I never had a problem with it myself, but some people were concerned over situations where the "true profile" had directly toleranced dimensions (like the included angle on a conical feature). Now we don't have to worry about that anymore, and we can just leave the runout definitions the way they are. If we need a progressing/offsetting zone on a cone or curved surface, we can use dynamic profile.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Ok, progression is not scaling, but it has this in common with uniform scaling: The size of the shape changes, while the proportions are kept. In the case of progression, the orientation and location are also kept. This is basically (pardon the pun here, too) what the documented rules say for the dynamic zone. Clearly for a planar tolerance zone the location can't be kept during uniform offset, arguably it is neither kept for an arc of a less than 180°. Then it is impossible to apply the same rules to all shapes.
Progression doesn't necessarily retain proportions. For an S-curve the concave part of the curve becomes smaller while the convex part becomes larger.
For any parametric curve, the convention is evaluating the normal vector from t=0 to t=1 at each t and generate a new point on the offset curve by a vector of uniform magnitude. This applies to straight lines, constant radius arcs, or any other higher order curve that might generate straight lines or constant radius arcs or splines/b-splines, or t-splines of any desired path.
In the slot examples there would be a common intersection point for all the different boundaries if proportions were kept; essentially a vanishing point for projective geometry. This is not the case.
For any parametric curve, the convention is evaluating the normal vector from t=0 to t=1 at each t and generate a new point on the offset curve by a vector of uniform magnitude. This applies to straight lines, constant radius arcs, or any other higher order curve that might generate straight lines or constant radius arcs or splines/b-splines, or t-splines of any desired path.
In the slot examples there would be a common intersection point for all the different boundaries if proportions were kept; essentially a vanishing point for projective geometry. This is not the case.
For an S proportions are not kept, but neither is the constant location as required for the dynamic tolerance zone. For a closed shape the proportions are kept and so is the location. The intent was most likely to keep the proportions constant, that's why scaling was considered by the committee before it was decided in progression, as Evan indicated.
- Status
Similar threads
- Question
- Locked
- Question
- Locked
- Question
- Locked
- Question