structuree
Structural
- Feb 20, 2022
- 10
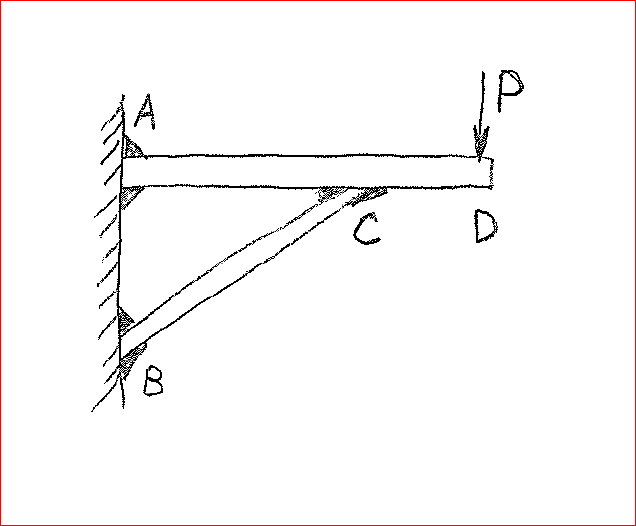
I'm trying to get my head around how pinned vs fixed connections appear in practise. I'm struggling to identify whether a connection will result in an induced moment. It doesn't always seem as straightforward in practise as it does in theory.
For example, I am aware that typically a connection with 2 x bolts would be designed as pinned, and you wouldn't consider it as taking any moment, but you add 4 or 6 bolts, and you're probably trying to crank moment into the connection. Where is the line drawn?
For example, I am aware that typically a connection with 2 x bolts would be designed as pinned, and you wouldn't consider it as taking any moment, but you add 4 or 6 bolts, and you're probably trying to crank moment into the connection. Where is the line drawn?



![[ponder] [ponder] [ponder]](/data/assets/smilies/ponder.gif)