-
1
- #1
LFRIII
Mechanical
- Sep 2, 2022
- 20
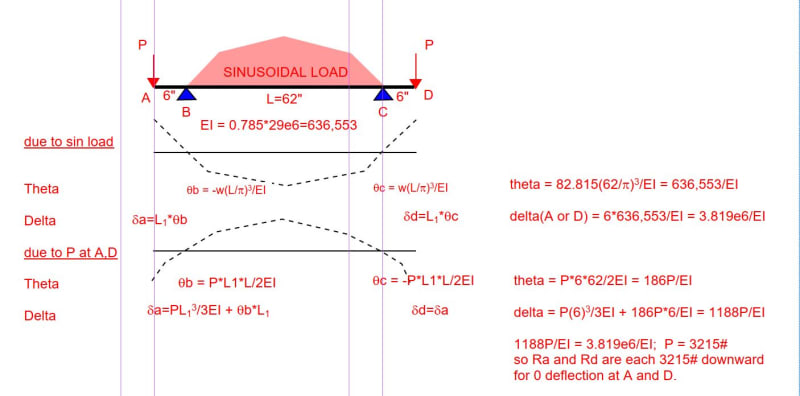
I am trying to solve the following problem which is in the method of superposition section of my Strength of Materials textbook. I am stuck and am wondering if anyone could point me in the right direction.
A beam of length 3L is supported by four supports, A, B, C, and D from left to right. The distance between any two supports is L. Between the two middle supports, B and C is a uniformly varying load with maximum intensity of w. Find reactions Ra and Rd.
I started by eliminating the two redundant reactions at A and D and used Case 10 Simple Beam with Uniformly Varying Load (see attached) to find the slope at points B and C. Then used Case 9 Simply Supported Beam with Couple Moment at End to find the moments a points B and C. From there I have tried many things without success.
The book gives the answer: Ra = wl/45; Rb = wl/36.
If anyone can help with this, I would appreciate it.
[URL unfurl="true"]https://res.cloudinary.com/engineering-com/image/upload/v1726255246/tips/Beam_Deflection_Formulae_iqr6vc.pdf[/url]
A beam of length 3L is supported by four supports, A, B, C, and D from left to right. The distance between any two supports is L. Between the two middle supports, B and C is a uniformly varying load with maximum intensity of w. Find reactions Ra and Rd.
I started by eliminating the two redundant reactions at A and D and used Case 10 Simple Beam with Uniformly Varying Load (see attached) to find the slope at points B and C. Then used Case 9 Simply Supported Beam with Couple Moment at End to find the moments a points B and C. From there I have tried many things without success.
The book gives the answer: Ra = wl/45; Rb = wl/36.
If anyone can help with this, I would appreciate it.
[URL unfurl="true"]https://res.cloudinary.com/engineering-com/image/upload/v1726255246/tips/Beam_Deflection_Formulae_iqr6vc.pdf[/url]