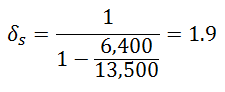hamza41
Civil/Environmental
- Jul 7, 2015
- 59
Hello,
I'd like to check the stability of RC columns against the reactions of a space frame. The columns' height is 12 m and their diameter is 60 cm. The issue is to decide the effective length factor value to adopt for this case to determine the critical buckling load Pc.
At first sight, the structure is sway as no bracing elements are present.
The question is: can I consider my structure as nonsway if it complies with the following condition (10-10) of ACI 318-11 and adopt an effective length factor of 1 instead of 2, or is this conditon only available for the determination of the Moment magnification procedure ?
Thank you.
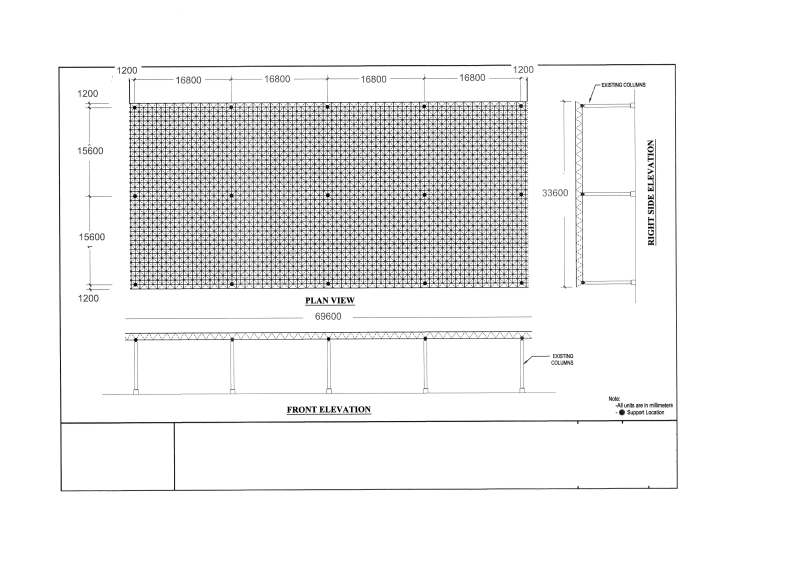

I'd like to check the stability of RC columns against the reactions of a space frame. The columns' height is 12 m and their diameter is 60 cm. The issue is to decide the effective length factor value to adopt for this case to determine the critical buckling load Pc.
At first sight, the structure is sway as no bracing elements are present.
The question is: can I consider my structure as nonsway if it complies with the following condition (10-10) of ACI 318-11 and adopt an effective length factor of 1 instead of 2, or is this conditon only available for the determination of the Moment magnification procedure ?
Thank you.