SeasonLee
Mechanical
- Sep 15, 2008
- 918
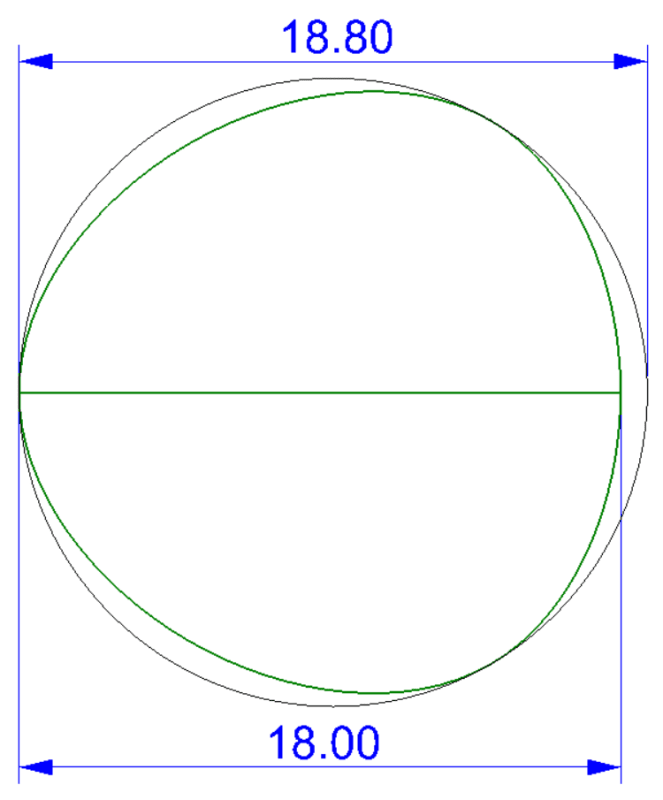
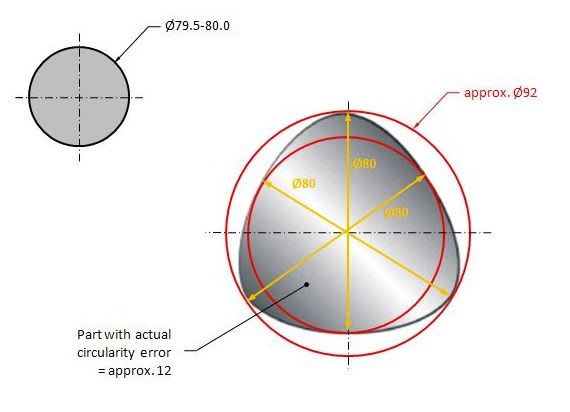
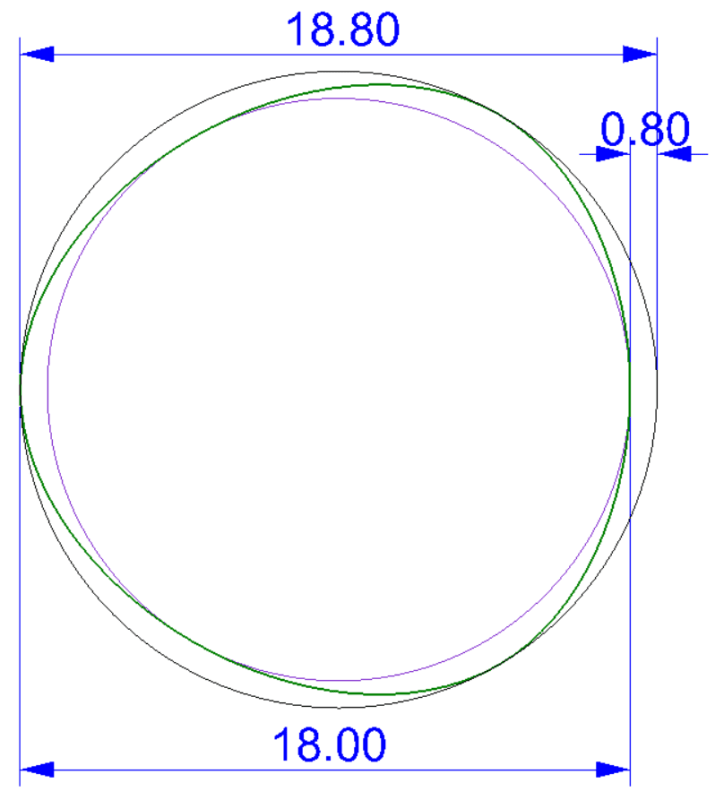
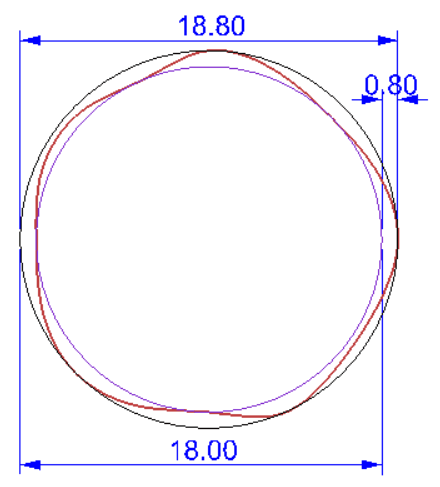
The figure below is a straightness callout on a shaft with a MMC modifier, but here I'm not talking about straightness, but circularity and cylindricity.
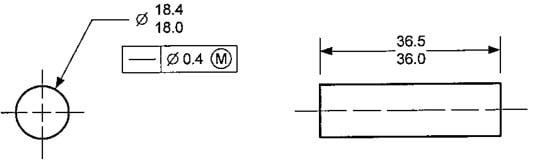
May I ask What are the maximum errors of circularity and cylindricity respectively.
Thanks for your help in advance
Season

May I ask What are the maximum errors of circularity and cylindricity respectively.
Thanks for your help in advance
Season