pandeydhiraj
Mechanical
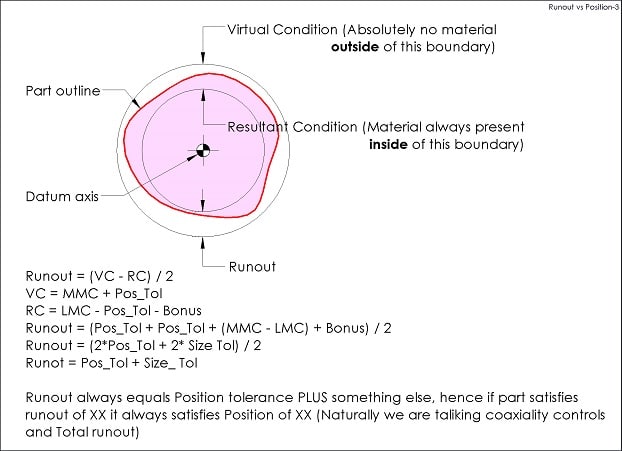
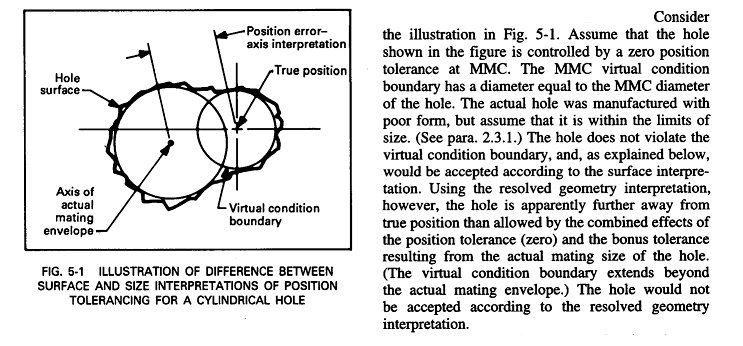
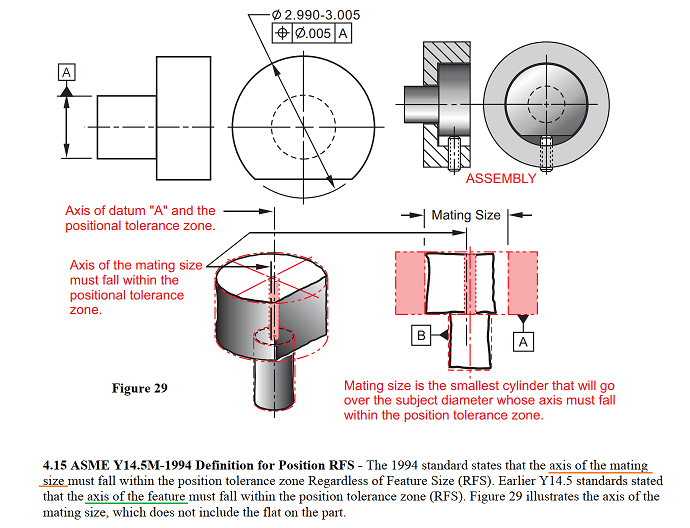
In any case can Position Tolerance and Run-Out can be applied together to a Feature of Size or plane surface.
I know both are location control doesnot make sense if applied to same feature, but just want to make sure about this thing.
Thanks
Dhiraj
I know both are location control doesnot make sense if applied to same feature, but just want to make sure about this thing.
Thanks
Dhiraj