FREE BODY DIAGRAM 1

[elinah34]

Hey,
I have a conceptual design, and I need to first check its potential strength.
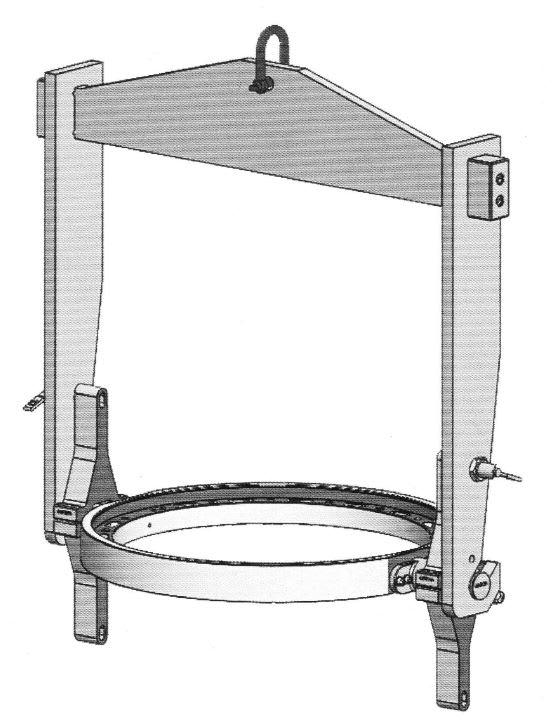
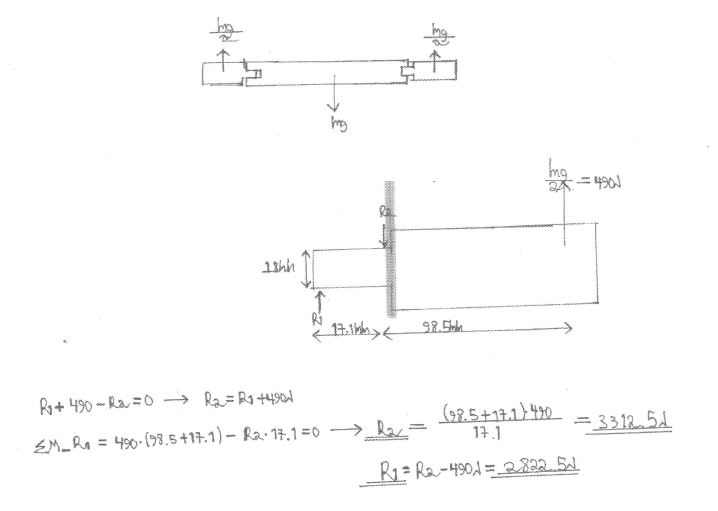
Here is a schematic picture of the conceptual design:

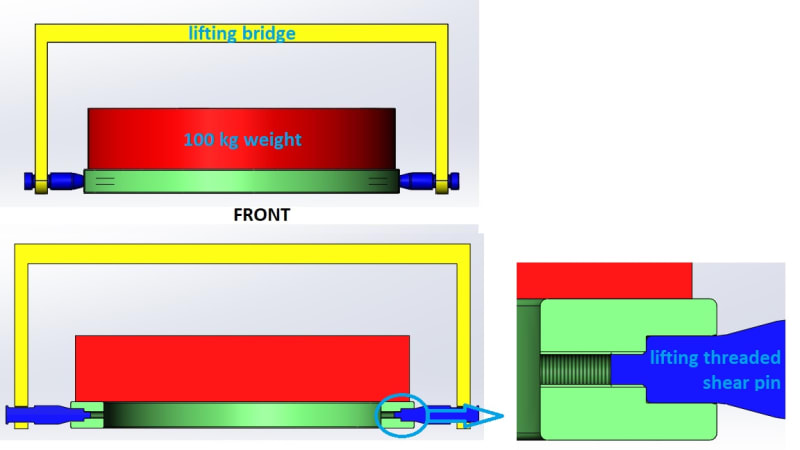
I have a lifting bridge for lifting the weight through its interface which has 2 Shear pins for taking the shear.
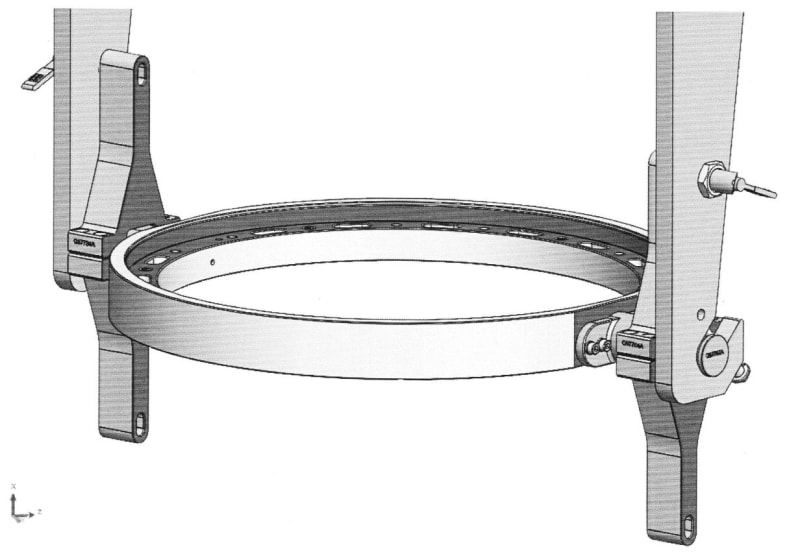
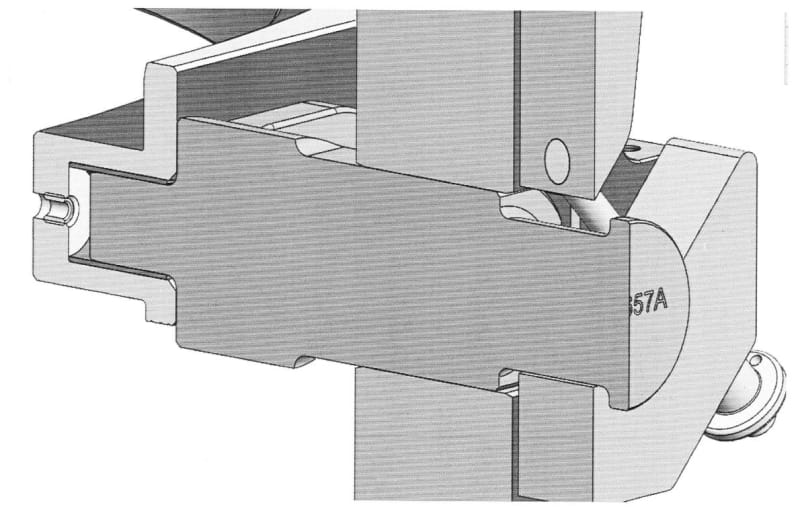
The Shaft/Hole fit (marked in purple in the picture below) is H7/g6, so there is a transition fit.

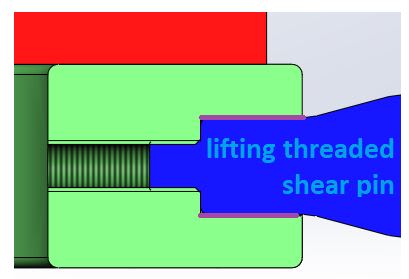
By the way, the thread is loose while the Shaft/Hole fit is tight, so theoretically the Shaft/Hole interface is the one to take the loads due to bending and not the thread, which is there only to axially secure the threaded pin in its place.
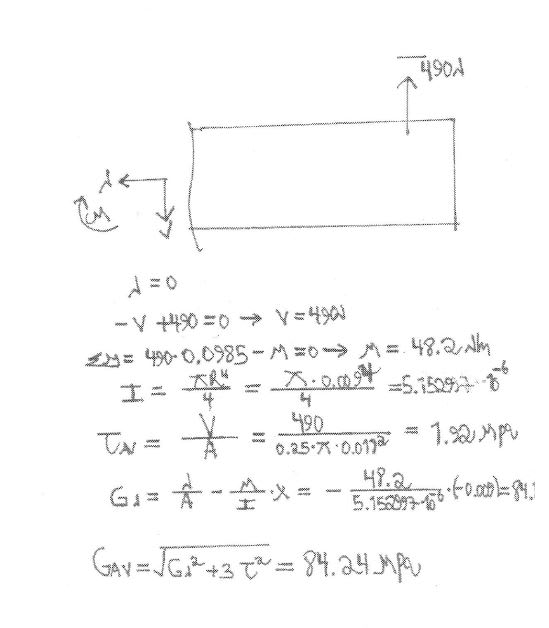
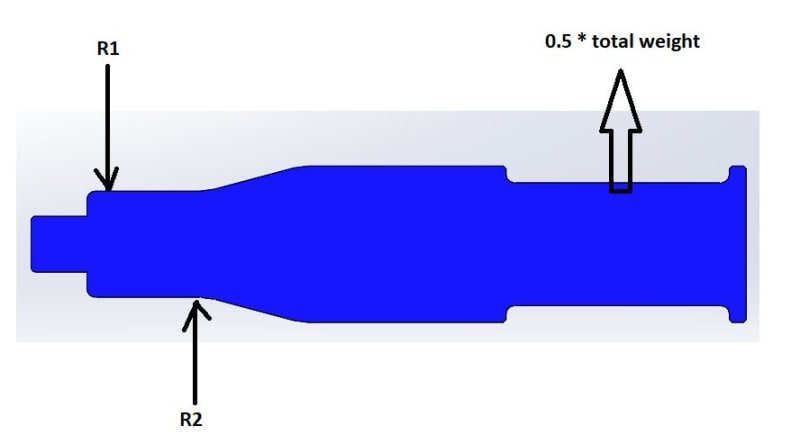
I tried to have a FBD (Free Body Diagram) of the threaded pin part, which I suppose is the critical one.
Here is a picture of my FBD:

Here I try to find the internal (in the critical cut) forces and moments by equilibrium:

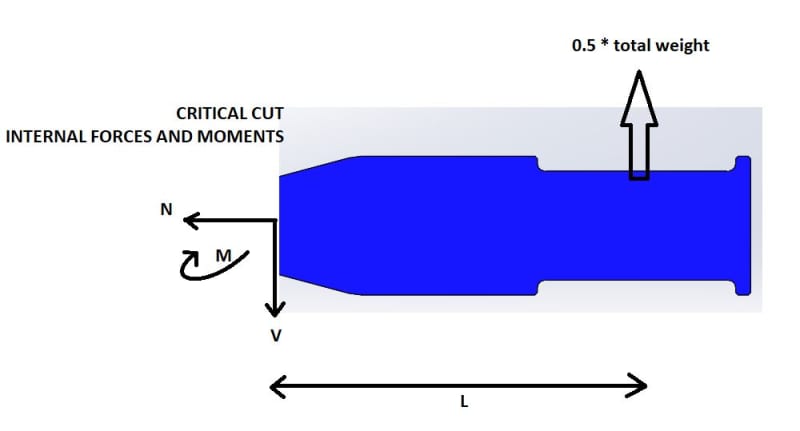
After finding V and M I find the shear stress and the normal stress using V/A and (M/I)*R correspondingly, and using von mizes relation sqrt(sigma^2 +3*tau^2) brings me to 80 Mpa.

The problem is that in the analysis I get around 25 Mpa.
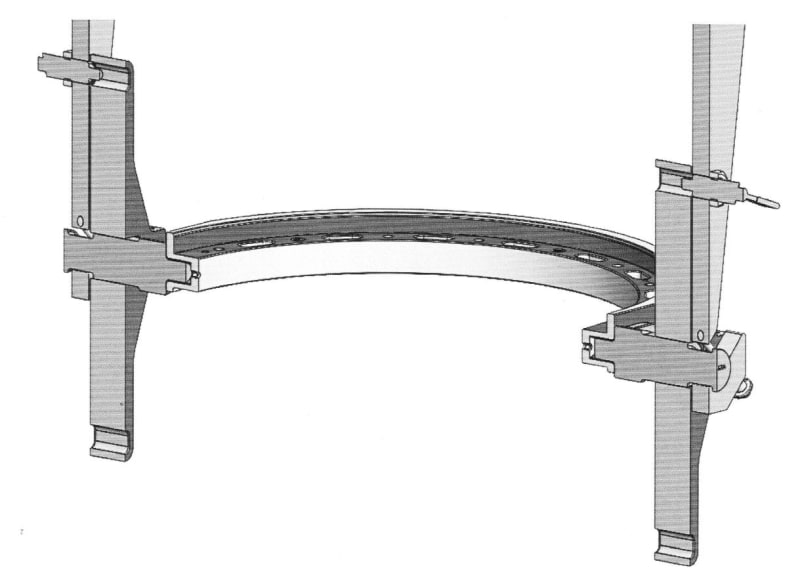
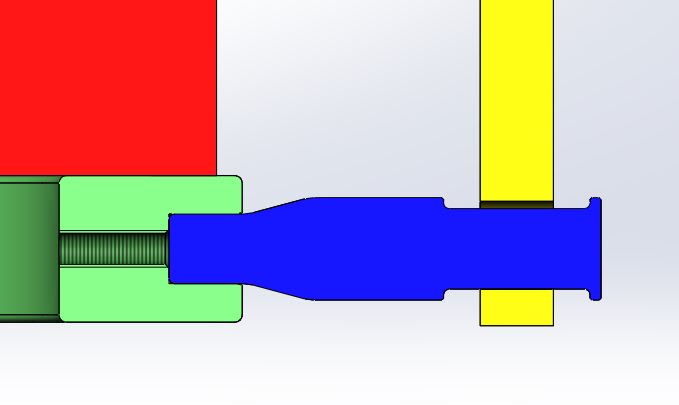
I have to point out that I already checked a configuration in which there isn't a thread at all (as in the picture below), and the results didn't change.

So I am interested to know which one might be mistaken - the calculation or the analysis?
I just hope you can help me by checking the calculation process I made.

Thanks

 

[rb1957]

why have a thread if the blue shaft is a tight fit in the green socket ?

is the blue shaft adjustable ? within the tight fit of the green socket ??

are you taking care to leave a space at the vertical face of the blue shaft ?
if not, then ...
1) this face is another loadpath for moment, and
2) you'll end up stripping threads (if you keep turning after the vertical face has seated.

you could consider a "jam nut", on the OML of the blue shaft.

another day in paradise, or is paradise one day closer ?

 

[elinah34]

rb1957
I am sorry but I don't understand your probably useful comments. What about the FBD? Any comments?

 

[BrianE22]

Any dimensions? Could be your first FBD is mostly correct. I think I would model it as a cantilever with a moment applied to the left end and R2 as shown.

 

[rb1957]

before you worry about the FBD, you have to worry about real things.

how does the thread work if there is a tight fit between the blue shaft and the green socket ?

if the blue in green is a permanent install, then the tight fit would work (I'd go for thermal interference).
But then you don't need the thread ?

if the blue in green has to dismantle, then you Can't have a tight fit.
So you should look to mechanical restraints, like cross bolts.

describing the moment restraint within the socket as a couple is "simplistic", and I'd rather keep it as a moment.

another day in paradise, or is paradise one day closer ?

 

[elinah34]

There is no interference, H7/g6 is a "sliding" fit, so dismantling shouldn't be a problem.
About moment instead of couple - I didn't say both reactions are identical, hence it's not a pure moment (a couple) but reaction forces as might be in the real case. In my opinion the bushing can't provide the pin with moment as suggested earlier, but only forces.
A moment as a reaction would be taken into account if, for example, the parts would be welded to each other.

 

[desertfox]

One problem I see is if the lifting pins are round and locate in the lifting frame, then what stops the loads along with the pins rotating within the liftingframe, put another way what holds the load horizontal while it’s being lifted?

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[elinah34]

desertfox
A good remark, and since I didn't model everything it seems missing. But in reality there is a plunger that does the work.

 

[rb1957]

a real world problem with a two point lift.

as to fits ... I read this "By the way, the thread is loose while the Shaft/Hole fit is tight".

can you expand this comment ... "After finding V and M I find the shear stress and the normal stress using V/A and (M/I)*R correspondingly, and using von mizes relation sqrt(sigma^2 +3*tau^2) brings me to 80 Mpa. The problem is that in the analysis I get around 25 Mpa."

are you saying a hand calc gets you 80MPa but FEA gets you 25 MPa ?
or worse are you saying the "answer" is 25 MPa ?? (if so the direction about homework)

what do you mean with "since I didn't model everything it seems missing" ?

relevant to your FBD ... what's the distance between R1 and R2 ?
a) the width of the blue/green overlap (as though the blue shaft has "cocked" in the (large) green socket hole, and is contacting at the extreme ends) ? or
b) 1/3 of the width ? (why would I think this ??)



another day in paradise, or is paradise one day closer ?

 

[desertfox]

Hi well if there is a plunger supporting the load then the load weight is not necessarily a two point lift, can you show the plunger on the model please.

Further we can’t check the 25Mpa without knowing size of pins etc, in principle the FBD a appears correct however the practicality of the lift frame and pins isn’t the best way forward. For example the concentricity of the thread to the
the toleranced pin diameter is critical because if the thread concentricity is out by more than the clearance between the bore and the pin then you won’t be able to assembly the pins to lift it. This statement also holds true for the tapped hole and the bore on load you are trying to lift.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[3DDave]

That free-body diagram - the one that shows reaction loads where gaps will be?

 

[SWComposites]

What “analysis” was used to get 25 MPa?

 

[elinah34]

Here are some photos of the design.
You can see that the lifting pin has a supporting flange with bolts.
But the Engineer who is in charge of the safety required calculating it as if there are no bolts and there is no support by the flange.
The motivation is making sure that improper use of the device may not immediately lead to a failure.

Here is a calculation of the stress in the critical cut under the assumptions above (reauired by safety).

 

[Compositepro]

It would all workout better if you used a taper fit rather than a clearance fit, with a straight start and hole.

 

[elinah34]

Compositepro, why?

 

[3DDave]

Since the bolts are on the neutral axis they don't help much. The thread is shown in bending, unlike the original problem statement; not an ideal condition as it creates a stress concentration, possibly 5 to 10 times the expected stress.

It looks to me like this arrangement will twist the ring and then the pin will sit at a substantial angle in the cradle.

Is this a copy of an existing product?

 

[rb1957]

yes, it looks sort of magical, but then I don't think we're seeing the complete story.

ok, your calc is 84 MPa, looks reasonable. why do you "think" the answer is 25 MPa ?

another day in paradise, or is paradise one day closer ?

 

[rather_be_riding]

I think you're close enough for a bush job on this one already but for the sake of debate I think your reaction will actually occur on the 'face' of the pin which mates with the outer ring diameter. I would treat the spigot end as a fail-safe should the 4? external fasteners fail to hold that joint tight.

This approach makes no difference to your hand calc which seems correct enough to me although I'd probably set my inital free-body diagram up a little differently as a result. It does make a difference to how tight the spigot fit needs to be (not very) and whether you develop concerning stress concentrations at the section step.

Why is the socket bushed? Curiousity only.

 

[desertfox]

Well it appears we agree with the analysis, however I still don’t understand how the whole bottom ring doesn’t rotate along with the flanged pins, sorry for my ignorance.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[rather_be_riding]

The pins are held in place by 4 SHCS (two each side) to the ring so the ring can't rotate relative to the pins. The pin in turn is restrained from rotation by the torque arm (clamped to the pin just inboard of the hook) which can be fixed in what appears to be two positions 180 degrees apart by the index plunger on the hook.