struct_eeyore
Structural
- Feb 21, 2017
- 268
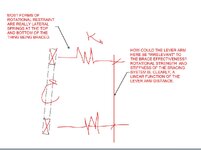
I have a series of wood trusses terminating on the interior of the building which have some very tall heels (13'+)
There is no shear transfer by design here - although some might occur in reality.
I'm leaning towards sheathing this section full height, but am wondering if that might be overkill - in lieu of X-bracing.
(truss profile is hatched in figure below)
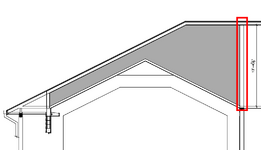
There is no shear transfer by design here - although some might occur in reality.
I'm leaning towards sheathing this section full height, but am wondering if that might be overkill - in lieu of X-bracing.
(truss profile is hatched in figure below)