Miami Pedestrian Bridge, Part IX 33

[JAE]

A continuation of our discussion of this failure. Best to read the other threads first to avoid rehashing things already discussed.

Part I
thread815-436595

Part II
thread815-436699

Part III
thread815-436802

Part IV
thread815-436924

Part V
thread815-437029

Part VI
thread815-438451

Part VII
thread815-438966

Part VIII
thread815-440072


Check out Eng-Tips Forum's Policies here:
faq731-376

 

[jrs_87]

May 16, 2019 ENR article by Scott Judy and Richard Korman

https://www.enr.com/articles/46867-spreading-cracks-on-fiu-bridge-failed-to-alarm-project-team

 

[Ingenuity]

In the May 16, 2019 ENR article linked by jrs_87 it has this quotation from Bill Gamble:

William L. Gamble, professor emeritus of civil and environmental engineering at the University of Illinois in Urbana, told ENR that he was “dumbfounded, greatly surprised and appalled” at the documents detailing the meeting, adding: “Yes, reinforced concrete structures often crack, but no, the cracks should not be large and growing day by day.

“I still find it hard to believe that anyone who had taken, and passed, a course on reinforced concrete design and behavior could not be greatly concerned,” he added. “Cracks that one can stick the end of a tape measure into are a collapse waiting to happen.”

Bold emphasis added by me.

 

[gwideman]

[Revised to add image of spreadsheet calcs, which correct a miscalculation in previous version. Basic conclusion remains the same].

OK structural people, could you take a look at this and tell us whether I've understood the following?

If I'm right, the crucial page of calculations that verifies sufficient strength of the strut-to-deck nodes seems to have some conspicuous problems.

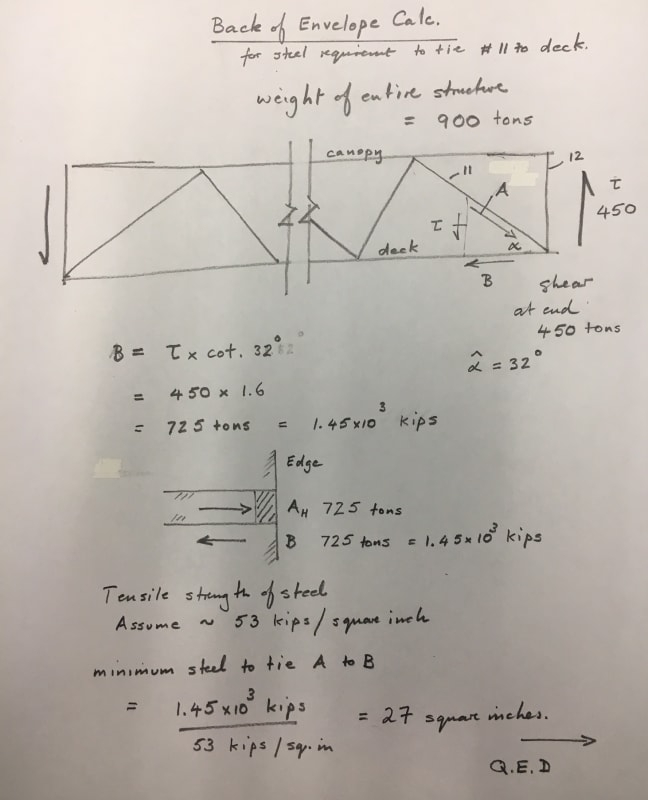
The other puzzle is that there are several areas where the number and spacing stirrups was done to keep the diagonals from rupturing, yet nothing about the amount of re-bar to take the shear loads at these locations.

I and others had been puzzled by not finding the calculations where the assessments of horizontal shear forces at 11/12/deck are compared to horizontal shear resistance provided across that plane by concrete friction and rebar.

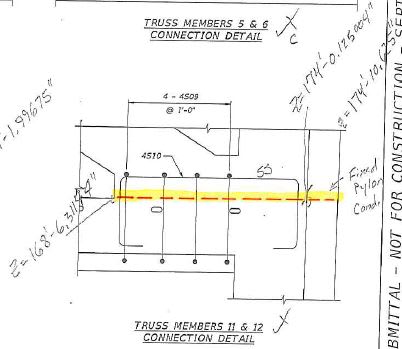
The relevant page appears to be: UCPP_Final_Calculations_Superstructure (1).pdf PDF Page 1284 (labeled 1283) where there are three tables listing and calculating several variables for each of the deck-to-member nodes.

It's a bit of a chore to understand all the variables, but they are described on pages PDF 1295 and following, though the example there is for vertical shear planes, and page 1284 is about horizontal shear planes.

(I also found a PDF 2012 copy of the AASHTO bridge manual which covers the same material, and is searchable for variable names:

http://www.ddzph.com/wp-content/upl...ge-Design-Specifications-6th-Ed-US-东大自平衡.pdf)

Description of variables and reasoning:

bvi: width of interface (21")

Lvi: Length of interface. For most of the nodes this matches the lengths shown on the drawings on PDF pages 1440 and 1441. Oddly, the lengths used for the end nodes are conspicuously shorter than the length on the drawings, but do correspond to the length over which the rebar is distributed, plus a modest amount. That oddity would underestimate the cohesion component of stress resistance, but that's zeroed out by c = 0.

Acv = bvi x Lvi Area of interface

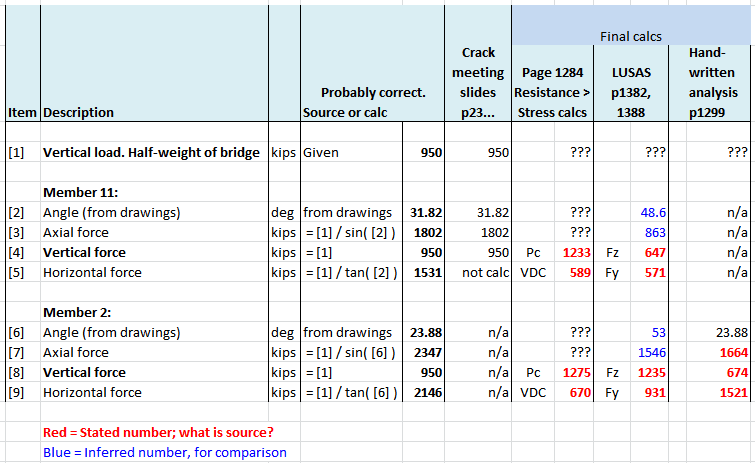
Pc: Compression force perpendicular to the shear interface. So in this case, the vertical component of Compression force in the diagonals. For the end diagonals 2 and 11, we would expect this to be half the bridge weight, or 950 kips. For 2 and 11, Pc is overstated at around 1250 kips, which I will come back to.

VDC, VLL, VPT, VTU+TD. These are apparently components of horizontal stress. VDC (stress due to dead load of structural components and any nonstructural attachments) looks extremely understated for members 2 and 11. Given a vertical load of 950 kips, and member angles less than 45 degrees, the horizontal component VDC has to be more than 950, not 589. And if Pc is supposedly around 1250, then VDC has to be more than that. (And in previous calcs I have shown it to be even higher.)

Vui: This is a crucial variable -- the total horizontal stress to be resisted.
Vui = the sum of VDC, VLL, VPT, VTU+TD multiplied by their respective load factors (provided in the "Load Factors" table.)

Needless to say, if VDC is understated, then so is Vui, by an even larger amount since DC load factor is 1.25.

Avf: Area of rebars passing through the shear plane. Avf tells the number of rebars, which are all #7 whose cross section is 0.6 sq-in. These correspond to the bars seen on PDF page 1448. None of the rebar area Avf figures look correct, and several of them are negative!

Since one of the purposes is to determine whether the rebars are sufficient, the fact negative rebar areas were not noticed seems to me a rather significant indication of the level of scrutiny this vitally important calculation underwent.

Lest we disbelieve that Avf is maybe not what I just described, continue on to the third table on the page.

Here the crucial variable is Vni, Nominal Interface Shear Resistance. One of the most crucial design checks is that shear resistance is greater than shear force, or Vni > Vui.

Vni = c x Acv + mu (Avf x fy + Pc) where

c (cohesion coefficient) = 0 for this analysis (making Acv moot, as previously noted)

mu = coefficient of friction = 1

Avf = area of rebar passing through the interface

fy = 60 ksi (shear resistance of rebar per area)

Pc = force normal to interface = 1233 for member 11. So note that overstating Pc by 30% means the shear resistance will be overstated by 30%

So Vni = 1 (-2.28 X 60 + 1233) = 1096.

Note that this matches the third table, showing that the calculation blithely subtracted the shear resistance of the negative rebars, verifying that Avf is indeed what I surmised!

The negative rebars error understates the shear resistance, hence would have made the bridge safer, but it also shows that effectively the shear resisting rebars were simply not calculated at all. So the calculations supposedly "validate" that all the shear resistance can come from the concrete friction resulting from the normal force, with no rebars.

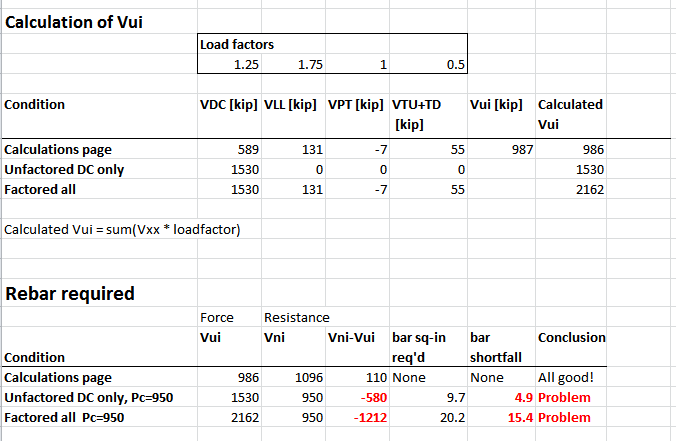
The following image shows several versions of the calculation of the shear force (Vui), and the implications when compared to Vni (shear resistance), and resulting rebar requirement.

Of note:

1. So far as I can tell, the bridge should have been designed according to the "factored all" row, in which case the provided 4.8 sq-in of rebar is 15.4 sq-in short of the requirement.

2. But as a better idea of whether the bridge should be able to stand up at all, we might neglect the live load, and the load factor, and just use raw VDC as the horizontal shear. That would result in a requirement for 9.7 sq-in of rebar, double what was provided. (The calculations page conservatively omits any reliance on concrete cohesion, so presumably there some additional shear resistance from that source not counted here.)

Summary:

[ul]
[li] The horizontal shear force VDC was stated as 589, clearly less than the 950 it would be for a 45 degree member (ie: no-calc reality check should fail), and hugely less than the 1531 I calculated for #11's actual angle of 32 degrees. [/li]
[li][/li]
[li] The horizontal shear resistance concrete friction component was overstated by 30% by overstating Pc. (But that error was reduced by the contribution of the "negative rebars".)[/li]
[li][/li]
[li] The rebar area was negative, which essentially means that so far as the calculations are concerned, the rebars were unnecessary for shear resistance, a clearly absurd result.[/li]
[/ul]

These problems appear so conspicuous that it seems hard to believe that these are the calculations actually used, or that these issues went unnoticed. Hence my interest in having someone with a structural background take a look.

 

[FortyYearsExperience]

An undergraduate engineering student from my time as a student, without any computing device, would easily have been able to arrive at the following result on the back of an envelope:

I think this tells us what has happened to college education in this field since the introduction of computers. Nobody today can "see" where the maximum forces and stresses in a structure are located. Engineers today wait for the color coded printout, without understanding that a back of the envelope calc. MUST be done in all cases to check that the order of magnitude is correct.

Tragedies will continue until colleges go back to teaching the old method of visualization and hand calculation of structural forces and stresses.

 

[FortyYearsExperience]

The calculation below took less than 10 minutes. The calculation is an "order of magnitude" check. It ignores live load, to provide a rapid check for absolute minimum steel required to tie diagonal 11 load to the deck load.
The calculation confirms the calculation above almost exactly. One could add factors and the like, but the correct answer is somewhere close to 28 square inches of steel needed to tie the compressive forces in diagonal 11 to the tensile forces running in the deck. NOT the 5 square inches actually provided.

 

[gwideman]

... 23.4 sq-in...

Thanks for commenting. As it happens I was in the process of tidying the spreadsheet I used, and discovered that I had applied the load factor for VDC twice. I have corrected that error in the post you commented on.

The general conclusion is the same. Just that the 23.4 sq-in should be "only" 15.4 sq-in.

And I think your sketch assumes that shear resistance is provided only by the steel, at 53 kips/sq-in, whereas the calculations page (and my calcs) get 950 kips of resistance from concrete friction under load of 950 kips, and use 60 kips/sq-in for the steel.

For what it's worth, 950 kips would be equivalent to 16 sq-in of steel. So that puts us both in the same ballpark.

 

[FortyYearsExperience]

Thanks for your interesting and thoughtful observations.

I believe however that the shear force between the tie and the deck is 1,450 kips, not 950 kips. (= one half weight of bridge, times cotan 32 degrees).

Also, I am puzzled that you find a reduction in shear can permissibly be attributed to concrete friction. The way I understand the shear capacity of reinforced concrete is to ignore the concrete when analyzing the steel. Then, do a separate check to see if the concrete can withstand the compression. In this case, I believe it cannot withstand the compression, but my check ends with the steel because it is hugely inadequate.

Appreciate any further thoughts.

 

[gwideman]

I believe however that the shear force between the tie and the deck is 1,450 kips, not 950 kips. (= one half weight of bridge, times cotan 32 degrees).

First, I think the 950 kips you're looking at is for Vni (resistance) not for shear force.

So the figure for plain horizontal force that I used was 1531 (not 1450), as follows:

I actually did it in two steps: 950 kips vertical --> 1802 kips diagonal --> 1531 kips horizontal. (This way I could match the diagonal force with a slide in the FIGGs "crack meeting" presentation).

However, to go directly:

Angle = 31.82 deg

Cotan(31.82 degrees) = 1.6115

Vertical force = 950

950 x 1.6115 = 1531 horizontal shear force.

 

[gwideman]

Also, I am puzzled that you find a reduction in shear can permissibly be attributed to concrete friction. The way I understand the shear capacity of reinforced concrete is to ignore the concrete when analyzing the steel.

I have very little background in this kind of analysis for actual materials. I'm just following what I recall from a first course in static forces, plus the calculations laid out on the referenced calculations page 1284, plus the description of the method in the AASHTO manual excerpt on pages 1295 and following.

So all I've really demonstrated is that the intended calculations suffer from wrong input data and wrong execution of the formulas that should have been calculated, producing results that seem so wrong (like negative rebar area) that they should have immediately triggered alarm.

I am not qualified to have an opinion on whether this was a suitable approach in the first place.

I think I have learned in this exercise that the shear resistance is seen to be composed of three parts:

1. Rebar shear resistance.
2. Friction at the shear interface (perpendicular force x friction coefficient)
3. Cohesion of the concrete, which is apparently not well characterized and thus controversial (and in calculations under discussion here, omitted).

I could certainly see how steel is the only component useful in tension. And maybe for assessing shear, there's a very conservative approach that again assumes the entire shear resistance would come from steel. But apparently that's not the approach taken here.

 

[FortyYearsExperience]

FIGG's calculations are extremely opaque, and this is evidently one of the sources of the problem. They could not even explain to themselves, in a checkable form, what they were calculating and why.

 

[gwideman]

FIGG's calculations are extremely opaque, and this is evidently one of the sources of the problem. They could not even explain to themselves, in a checkable form, what they were calculating and why.

Well I found the calcs a bit opaque at first. But after looking up what all the variables mean, it seems straightforward. It's also the same set of steps used on pdf page 1299, and also on the slides in the FIGG "cracks" meeting, albeit examining different shear planes. I infer that people who work with these variables everyday would find this easy to follow.

Though it is curious that the cracks meeting presented an examination (meeting PDF slides page 27 and following) of a different shear interface, rather than using the ones for which calculations were already available. (And as I've discussed earlier, the slides appear to overstate the shear interface areas, the perpendicular ("clamping") force and the rebars crossing the interface.)

 

[TheGreenLama]

I would even question the use of the 4 - #7 stirrups as contributing to the area of shear steel, the way they are detailed. The requirement states that the steel should cross the expected shear plane perpendicularly, AND that the steel be fully developed on either side of that plane. It's not clear from the design drawings how far the stirrups extend above the top of deck. Simply extending them above the deck construction joint (1" or 2" or 3") is not enough. To be fully developed (90-deg. bend) they'd need to extend at least 11" above the deck. And, if you wanted to use the steel coming from the diagonal for this purpose (that's assuming those J-bars are placed properly and fully developed), because they're crossing the shear plane at an angle, I would reduce the effective area based on the angle of the incoming diagonal--say use only 32/90 of those bars.

Is it clear where FIGG is pulling the numbers from for doing these calcs? I've looked through parts of the calcs only briefly. Page after page of tabular data cause my eyes to glaze over. Any thoughts on why 2 computer models were done. I haven't looked at the FEA at all, except to note that it's undated, done by someone else (not the LARSA modeler), and models only stage 1 of construction.

 

[FortyYearsExperience]

I would even question the use of the 4 - #7 stirrups as contributing to the area of shear steel, the way they are detailed. The requirement states that the steel should cross the expected shear plane perpendicularly, AND that the steel be fully developed on either side of that plane.

I entirely agree. There is, in reality, zero amount of steel provided to tie diagonal 11 to the deck.

 

[jrs_87]

Reinforced concrete beam resisting bending - BE of Reinforced Concrete with Prof Ibell Pt2

https://youtu.be/GPOAelSOLFs?t=69

Insightful explanation of how to control failure mode of reinforced concrete beams.

Has anyone here seen any evidence the emergency center-line shims were actuality installed and when? Is it possible the shim jack was being operated in conjunction with the PT rod operation? Obviously the diagram would have to be lifted some order of magnitude to fit the shim effectively.

Bear with me for a moment... I have faith in Figg in so far as engineering goes. I argue they think just like us and it rarely is useful to underestimate people. When they decide it's necessary to shim center-line, implement an "exoskeleton" to add confinement to 11/12 node, and get CIP tied in ASAP, I believe them on that. These recommendations suggest they knew what was wrong even if candor may have been lacking to some extent.

It's my opinion most structure engineers and construction managers would have resisted group-think and taken action to get road closed immediately upon examining that diagonal no matter what. It's just by fate none on this project quite reached that level. Possibly because closing the road was paramount to realizing structure was doomed and un-repairable.

 

[jrs_87]

GWIDEMAN: Here are some excellent lectures to assist in your quest.

https://www.youtube.com/channel/UCIL0NyWPPAqrikLb6hJMA8Q/videos

Video lectures are by David Garber, PhD, assistant professor at FIU (coincidence, link not submitted to be provocative)

 

[MikeW7]

I must have missed this earlier, but FIU is a research hub for ABC - Accelerated Bridge Construction - and does research sponsored by the US Dept of Transportation. David Garber, mentioned by jrs_87 above, is an Assistant Professor of Structural Engineering and a member of the Accelerated Bridge Construction University Transportation Center.

Whenever "FIU" has been mentioned in conjunction with the design of this bridge, I just assumed it meant the university administration, but now it looks like the bridge may have been intended to be some sort of recruiting showpiece for the FIU Engineering Department. In any case, I wonder how many of their faculty have left after this debacle.

EDIT ADD: This Miami Herald Article from 2018 March 15 reported that a university spokesman said, just after the span was installed, that the FIU ABC center was not formally involved in the bridge project. Below is a section from the article:

FIU’s engineering school has become a hub for accelerated bridge construction training and research in recent years.

In 2010, after recognizing the need for more engineers trained in the method, FIU started a center focused on the approach. It has drawn 4,000 people to its webinars since launching in 2011, according to a center website, and in 2016 became one of just 20 programs nationwide to receive federal funding amounting to $10 million over five years.

The center’s director, Atorod Azizinamini, recognized by the White House in 2016 as one of the world’s leading bridge engineers, said the method is safer and more efficient than conventional construction.

[highlight #E9B96E]“We are able to replace or retrofit bridges without affecting traffic, while providing safety for motorists and workers who are on site,” he said in a 2016 press release about the program. “The result is more durable bridges.”[/highlight]​

 

[gwideman]

At this point I'm fairly satisfied that, as described in my earlier post, UCPP_Final_Calculations_Superstructure (1).pdf PDF Page 1284 (labeled 1283) is where the stress resistance is supposedly checked against the stress demand, and wrongly passed due to wrong input numbers.

So I agree with:

Is it clear where FIGG is pulling the numbers from for doing these calcs?

... that one point of interest now is where did those numbers come from?

In summary, the numbers that I think are of most interest are the red ones in the following table:

Here I show what I think are the correct values for key variables, and the four calculations that we've seen presented. (I've included the calculations pertaining to member #2, because it allows comparison to the handwritten notes page.)

Clearly the biggest puzzle is how the half-weight of the bridge was not the number used in the key calculations. The angles of the members were also wrong with a comparably harmful effect on the calculations.

A related issue is how the rebar area on page 1284 came out negative, which is impossible. That didn't help the bridge to pass muster, but it does imply incorrect formulas behind the result table, and thus a flawed process in setting up this critical design-check report and also the checking of it, both of which would make illuminating lessons.

 

[TheGreenLama]

Some general thoughts on approach and speculation on load disparities.
Two different shear planes, two different approaches to design.

Shear Plane 2 (as imagined on p.1298 of calcs)

External loads are applied to hand-drawn free body diagram.
Easy to visualize. Easy to get a feel for relative load magnitudes.
Presume loads are taken from 2D LARSA.


Shear Plane 1 (as shown on p.1381 of calcs)

Member 11-12 area is modeled as a 3D block in the FEM.
From within this concrete block a "slice" is defined.
Loads are extracted for this "slice", taken as gospel, and used for design.
No attempt made to gauge relative magnitudes of extracted values to real world numbers.

From the table on p.1283, Acv (concrete shear area) = 882 sq in, with Lvi = 42 in
This 42 in corresponds only to the area where the #7 stirrups are situated.
Could it be that Shear Plane 1 was checked using only the load over this area, excluding the Member 12 area?
Could it be that Shear Plane 1 was checked for fixed pylon case?
Could it be that the unaccounted for Member 11 load, which needs to be designed for, is just not crossing this plane slice due to modeling irregularities?
[Edit: Using this internal slice method to extract loads, is it conceivable that the longitudinal PT in the deck is impacting (i.e. incorrectly reducing) the design shear load on this internal slice?]

And, Gwideman, I agree that when looking at this puzzle it's good to incorporate Member 2 in the summaries, for comparison purposes.

 

[gwideman]

p1298 of calcs... Shear Plane 1... Presume loads are taken from 2D LARSA.

(aka PDF page 1299)

I agree that the free body diagram is satisfyingly visualizable. But it uses a vertical load of only 674 kips (and correspondingly low axial force).

p1381 of calcs ... Could it be that Shear Plane 1 was checked using only the load over this area, excluding the Member 12 area? Could it be that Shear Plane 1 was checked for fixed pylon case?

(aka PDF page 1382)

I wondered those points too. But the vertical load on #12, while substantial, would surely be only a small fraction of the 950 kips half-weight of bridge.
And somewhat countering the pylon speculation is that the interface length chosen is only 5'-5.8", which includes the entire dashed red line, excluding the fixed pylon.

I did search the entire calculations PDF for the key numbers I've highlighted previously in red, and found none of them. (And when looking for "647" for example, I searched for "647", and also "646.", on the basis that the page 1382 calc might round up.)

 

[jrs_87]

Member 11 is offset from diaphragm support. Would areas I marked in orange also be subject to shear? Does anyone know where the steel for this is detailed? And would not the PT bars have messed with this?

Also, does not the offset of 11 and diaphragm greatly reduce vertical vector of clamping force against shear in yellow area? The diaphragm on south size was much larger because it did not share space with CIP wire stay pylon/tower.