Miami Pedestrian Bridge, Part XIII 81

[JAE]

A continuation of our discussion of this failure. Best to read the other threads first to avoid rehashing things already discussed.

Part I
thread815-436595

Part II
thread815-436699

Part III
thread815-436802

Part IV
thread815-436924

Part V
thread815-437029

Part VI
thread815-438451

Part VII
thread815-438966

Part VIII
thread815-440072

Part IX
thread815-451175

Part X
thread815-454618

Part XI
thread815-454998

Part XII
thread815-455746


Check out Eng-Tips Forum's Policies here:
faq731-376

 

[FortyYearsExperience]

*The debate above is focused on the supposedly "correct" angle that the dry joint should have followed.
*Referring to the drawings below, the debate seems to be that the dry joint should have followed the orange plane, and not the blue plane.
*This debate is irrelevant because the failure did not occur along the blue plane; and, the orange plane would have made no difference.
*The joint failed along the two red planes identified in the Side elevation and the Top View.
*Specifically, the surfaces that failed under sheer load are the two surfaces identified as having dimensions b x c
*If you calculate how much steel is required to hold 1500 kips in strut #11 from moving northwards, you will find it needs about 25 square inches of steel.
*If you study the drawings, you will find perhaps 5 square inches of steel crossing the red planes (b x c) that might act as an anchor against strut #11 moving northwards. The concrete itself adds no resistance, because across these red planes, there is no clamping force.
QED

 

[ldeem]

For the folks with a lot of concrete experience - what do you think of a shear key in such a critical cold joint?

I have read though some of the reports online and would like to learn something from this to improve my own designs. So far the main takeaway I have is that where critical constriction processes are needed (such as roughing the surface) to call it out instead of referencing standards.
The second takeaway I have is using shear keys any time I have a critical cold joint.

 

[Earth314159]

Forty years of experience,

I am not quite sure what you mean. The failure plane was the blue plane. Figg actually did a calc on the pink planes in their presentation just before the collapse. It was not a critical link in the chain. They missed the blue plane which was the weak link in the load path.

There is a clamping force from the transverse PT that rests shear friction through the pink planes. The is also a tonne of bars in the deck and diaphragm. The shear stress is substantially less since there are two shear planes. The mu value is also much higher since is part of a monolithic pour.

 

[Earth314159]

Ideem,

It is good practice in such a situation to use keyways. Our code does not have a means of calculating the shear friction at a keyway. It is part cold joint and part monolithic. It adds capacity but calculating the shear resistance is not necessarily easy.

Beware, using keyways can cause issues as well. The contractor can accidentally leave the wood blocks in place which makes the joint worse off. I don't like keyways where they aren't a significant benefit. I use to see them at strip footing and wall joints but these joints have low shear and it isn't necessary. That practice has tended to fall to the wayside.

 

[FortyYearsExperience]

Figg actually did a calc on the pink planes in their presentation just before the collapse. It was not a critical link in the chain.

Figg's calcs are worth nothing. That is why there was a collapse killing six innocents in the first place.

If you look at the cracking that was observed (see 1st photo below), you see that it passes through the two pink planes at 45 degrees (see 2nd drawing below).

There are NO photographs of the cracks passing through the blue plane - obviously, because none were observed.

Also, my point is that there is missing an amount of about 25 square inches of steel to TIE back strut #11 to the deck. Strut #11, with 15000 kips (15 million pounds) is simply not connected to the deck for any tensile forces. You can almost see strut #11 moving northwards in real time for want of being tied to the deck. This is proof positive.

There was not "a tonne of bars" crossing the pink plane. If you look at the relevant drawings, there were maximmum five (5) square inches of steel crossing the pink plane, and all of those were too short to develop any tensile load in those bars.

 

[Earth314159]

Forty Years of Experience,

The calculations done by Figg on the pink failure plane were not incorrect. It just wasn't the critical failure plane. They calculated the strength of the wrong link in the chain. It is the pour joint that is critical. The area is less, the steel through the joint is less and the mu value is less. The north end of the failure plane near #12 did punch but that was because there was a concentration of vertical steel in #12. The primary failure plane was the blue plane. The vertical steel in #12 was what held it together until the PT in #11 was re-tightened.

There is tonnes of capacity in the pink plane. It was never an issue. The #11 diagonal itself would fail in shear before the pink plane.

 

[Tomfh]

Earth,

Yep. Shear friction is upper bound, yet people treat it as lower bound.

You can’t just consider one failure surface. You have to consider all of them.

 

[TheGreenLama]

Earth, you are 100% correct. It's amazing that we're still arguing failure planes at this point in the thread.

My question w/ the FHWA 73, on page 84 in Table 3, they list Avf available for shear capacity. At all nodes they consider the bent #6 & #7 bars as engaged and fully developed. I would question this finding and argue against incorporating these bars into any Avf shear capacity. Or maybe if you were to use them, use them only at some fraction of their whole. IMO, they are not properly developed on either side of the shear failure plane, as required by code.

 

[FortyYearsExperience]

It just wasn't the critical failure plane.

If the pink plane was not the critical failure plane, then:

1. How come the photographs show catastrophic failure across that plane?

2. How come there are no photographs of catastrophic failure across the blue plane?

 

[Earth314159]

You can’t just consider one failure surface.

You are correct. I wouldn't such otherwise. However, there are literally an infinite number of possible failure planes. As an engineer you have to rationalize the failure planes that need to be checked. I am also not suggesting you shouldn't or don't need to check the pink planes of failure.

 

[Earth314159]

If the pink plane was not the critical failure plane, then:

1. How come the photographs show catastrophic failure across that plane?

2. How come there are no photographs of catastrophic failure across the blue plane?

1) I already answered this earlier. #12 has a concentration of vertical steel which helps transfer loads across the blue plane but this is just below #12 and not the rest of the shear plane. That is why you get localized punching at #12.

2) There are photographs of catastrophic failure across the blue plane.

 

[FortyYearsExperience]

2) There are photographs of catastrophic failure across the blue plane.

Really? Can you pass those on? I have studied all the photographs carefully. They are not in the record.

 

[3DDave]

Forty - what do you consider as "the blue plane"?

 

[Earth314159]

Fortyyearsexperience,

Check out page 96 of the OSHA report. This photos is other places as well.

https://www.osha.gov/doc/engineering/pdf/2019_r_03.pdf

 

[Vance Wiley]

Regarding your comment about using keys - would not an equally balanced key design with half area in one member and equal area in the other member leave only half the area for shear? Of course, with one part as a finite area and the other as a deck with relatively unlimited area, the key could be all of the smaller member and be a formed socket the size of the node. The benefit then would seem to be the contribution of the bearing at the loaded side of the socket.
My point would be to check the shear in whatever section remains to resist shears.
Thank you.

 

[Earth314159]

HI Vance Wiley,

I am not sure a fully understand. However, when I do a key design I will use 2x4s spaced at 7" centres (or 2x6 spaced at 11" centres) oriented perpendicular to the shear force. That way, the shear is forced to go through about the same amount of monolithic concrete from the first and second pour. I am not sure if that what you means by an equally balanced key design. If you have just one big key, it is just pushing out one end and you are back to the same/similar problem. If that you what you are saying, then I agree.

 

[FortyYearsExperience]

Check out page 96 of the OSHA report. This photos is other places as well.

Earth314, the photographs at page 96 show that the failure plane was on a combination of the blue plane and the pink plane. Close to the green plane shown below.

However, the fact is that we have a horizontal force in strut #11 of 1,500 kips going north. For equilibrium, we must have enough resistance to hold 1,500 kips onto the deck going south. Therefore, we must find 25 square inches of steel configured to pull in a southerly direction into the plane of the deck. Those 25 square inches must somehow CONNECT to the load in strut #11. The vertical bars in strut #12 have no southerly component and so don't count towards this requirement.

Is it being suggested that by roughing up the surface of the concrete at the blue plane cold joint before pouring strut #11, this would be sufficient to eliminate the need for 25 square inches of steel pulling south?

 

[Vance Wiley]

Shear Friction issues.
This was previously posted and deleted so I could clarify items. Here it is again.

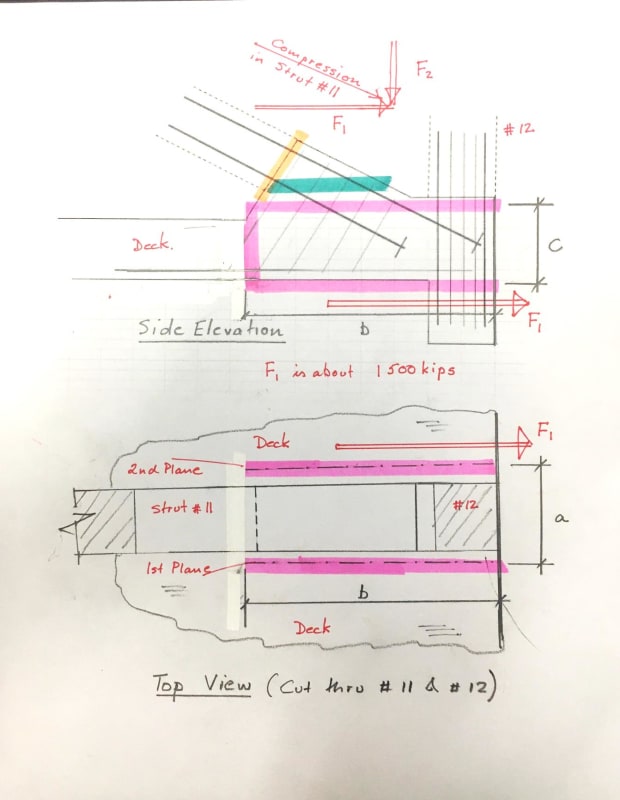
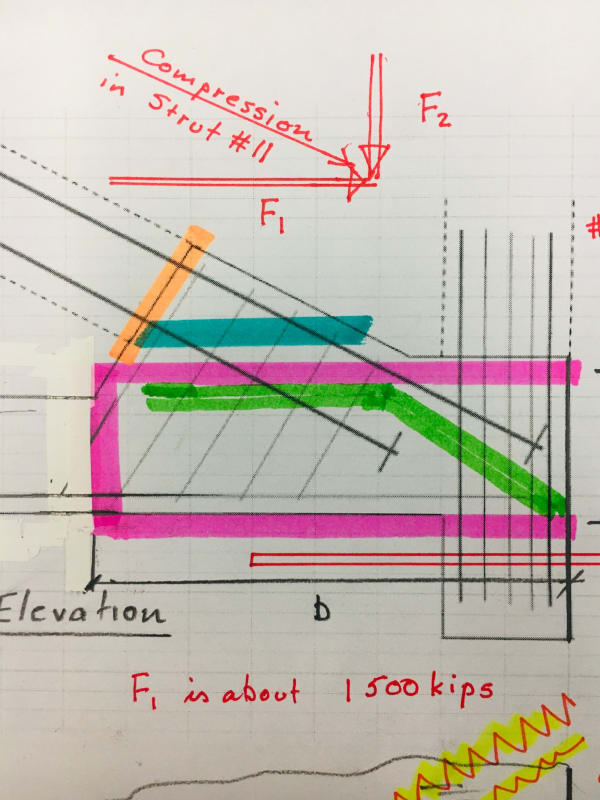
The subject of clamping force on the sides of the assumed shear plane where 11 and 12 punch thru and out the end of the deck is interesting to me. The conditions surrounding this failure provide an opportunity to examine the concept of shear friction. I would like to discuss, hopefully not alone, the shear friction concept as it could apply to a "clean" version of the FIU bridge, north end of main span.
The conditions at hand are certainly not 'clean' as this was a multi phased failure with prior cracking at the deck surface for one zone, failure plane defined by the void created by the lower PT duct in member 11, the presence of 4 - 4" dia pvc ducts, proximity to the end of the structure, and presence of already cracked end diaphragm 2, to list a few.
If this were to have occured in an area of deck fully surrounding the zone, it would have been much like a column in a flat slab. Failure would be mostly in diagonal tension and be reinforced for that. Portions of this failure developed into diagonal tension as it neared the edge or end of the deck, and that zone was already cracked by the load in the diaphragm. The diaphragm cracking may have loosened things up for the blow out - or maybe the other way around.

For for discussion and clarity, I would like to just discuss the shear friction issue. My purpose is not to declare some concept as the final thoughts but rather to elicit discussion and consideration of conditions unique to a simplified modeling of this failure. There are many present here with experience, understanding, and inquisitive natures with much to contribute. I hope something in this will interest you.

If reinforcing steel across the shear friction plane can provide shear capacity because it goes into tension and that is measured by 0.9 times yield or 57,000 psi lets see how much stretch that requires to develop 57000 psi (or whatever - the principle remains). Using a #7 bar and development of maybe 24D = 1.12"X24 =27 inches. If tension in the steel is zero at the embedded tip and 57,000 psi at the interface, the average is 28,500 psi and stretch is 28500X27/29,000,000=0.026 inches on one side. Then if the same embedment stretch develops in the other side of the interface there is a total of 2X0.026=0.052 inches gap in the interface at full factored resistance.
Of course if the surfaces have separated by 52/1000 of an inch we can now disregard any cohesion contribution.
I suspect the actual development length is less than that required by code, so lets say it actually develops fully in 12 diameters, so the stretch is half that just calculated, or total gap = 0.026 inches.
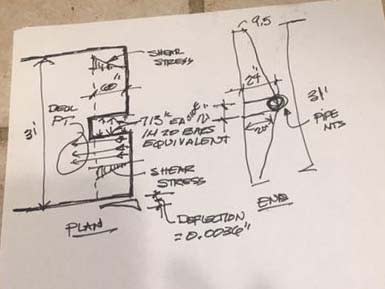
For the specific but simplified condition at hand, consider the deck as a monolithic flat member that is 31 feet wide, thickness varying from 9.5 inches at edge to 24" at center with a notch cut out for members 11 and 12. That notch is about 21" wide and 60 inches in length measured from the end of the deck and goes all way through. And lets consider that 25 total sq inches of reinforcing should cross the two interface planes if we cast the notch then pour members 11 and 12 into that notch and try to push them thru. We will adjust for monolithic vs intentionally roughened vs as cast conditions after the concept is defined, which I hope is about now.
So to support aggregate interlock in the two planes each side of the 21 x 60 notch, with those planes being 24" x 60" each, we can provide 12.5 sq in of reinforcing crossing thru each side. That reinforcing can allow - in a two part isolated shear plane condition - a gap of 0.026 inches and still function as a shear friction joint. (according to codes).
But lets disregard any steel and just let the shear capacity of the deck on each side of the notch provide resistance to the movement which would have stretched the steel across the assumed shear planes by 0.026 inches.
12.5 sq in of steel at 57 ksi is 713 kips each side. Average thickness of the deck each side of the notch is (24+9.5)/2 and 14 feet long from notch to edge of deck and that is 16.75" avg X 14'X12= 2800 sq inches. The shear stress in that section from the equivalent 713 kips is 713000/2800 =255 psi. It varies from 0 at the edge to 255 psi at the end of the notch, 60 " from the edge. Shear deflection at the edge will be tne average stress X length of loaded section (60") /Ev of 0.4X5,300,000 or 255/2X60"/(.4X5300000) = 0.0036 inches. That is about one seventh (0.14) of the stretch in the reinforcing which would cross the plane and still meet shear friction design concepts.
There is no active clamping force in this zone because the transverse PT begins just south of the cut out notch zone we have defined. And the shear deformation in the protruding flanges is zero at the end of the notch where the deck is 31 feet wide without a notch. So the average deformation from this spreading shear is far less than the stretch required to produce tension in the cross plane reinforcing. The longitudinal deck PT crosses the plane in the deck at maximum "spread shear" at 60 " from the end so bending moment in the protruding flange is negligible and the shear deformation is the major factor. That longitudinal PT provides an active clamping force for the shear in the deck extensions.

So the questions that arise include:
1) If passive reinforcing across a defined or assumed shear plane can provide shear resistance by developing or retaining a condition of restrained contact and thereby contribute to shear capacity of that plane, can other conditions which create similar restraint contribute also? And if not, why is the reinforcing allowed to do so?
2) Should bar sizes across a defined plane of shear friction be limited in size? Smaller bars develop full capacity in shorter lengths and therefore the stretch is less.
3) If developing the tension in the reinforcing across an actual created joint causes stretch in that reinforcing (I see no other way) with some corresponding separation of mating surfaces, why is cohesion even considered to act in conjunction with the reinforcing?
4) Is the shear friction design based more on formulas which attempt to define what was learned in test results and less on engineering logic? (Dare I challenge the gods?)
5) Is something bad wrong with my logic or calculations? This should be a gimmie - hint: Very probably.

Thank you. I would really appreciate comments.

 

[Vance Wiley]

You describe conditions detailed on a standard detail we used many many times. The shear is resisted by the later placed mating pour of concrete which fills the formed key. That amount of concrete in shear should have the capacity to resist the shear.
Combining the keys with formed surface coeff of friction and reinforcing across the joint would create a shear friction design. I do not know of anyone combining keys and coeff of friction. I wonder what AASHTO would think?
Thank you.

 

[Vance Wiley]

You are correct - they do not appear to meet development requirements - but those really involved in node 11/12 appear to have failed at the deck surface so they developed everything available. One question is why is node 11/12 the one with the least number of those #7 bars across the joint?
If they were given a proportionate value as you suggest, there might have been more of them and that would have helped.