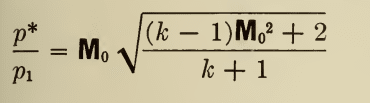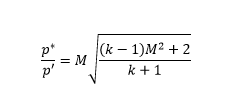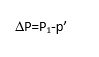TomaszKruk
Civil/Environmental
- Oct 2, 2019
- 33
Hello,
I have a problem to solve that seemed trivial at first, but kinda got out of hand quickly. I want to properly calculate pressure drop on a gas pipe on a chemical plant. I thought I'd find "plug and play" equations with iterations maybe, but after 2 days of reading I'm horribly confused.
Can someone point me into a direction of a legit source for compressible flow pressure drop equation? There will be no outlet to atmosphere, no flare - I need to calculate exact value of pressure drop on the line so the equipment downstream from my pipe won't work above design conditions. I did not select the working pressure or design the equipment downstream - all I got is obvious conclusions that I need a certain loss value or things might look bad.
I tried an older version (that is the one available for me) of the 410TP. Simple Darcy equation is easy enough to solve but untrustworhy. Darcy formula including Y factor is infuriating - you need to know the pressure drop in order to calculate Y, so the equation is useless to me.
I did solve a verion of the Isothermal flow equation provided, all good and well, but my spreadsheet is acting funny (probably excel finds it hard to iterate solution since I work with SI units and my pressure is around 40 bar - the equation works for Pa only). I'd like to verify the results. Especially that I suspect it works best for mass flow calculations, if the pressure loss is given.
I found a webpage with free calc, but it gave me an error I'm too dumb to understand (supersonic outflow?). I even went thru the process of learning to use "." instead of "," and the Imperial units for it
I read a lot of sources but most of them I suspect are viable only for natural gas even though they do not state that directly (like Panhandle equation - I always believed it works for natural gas only, but there it was in a paper about gas flow thru pipes).
Gonna go with this one next:
Please help guys - this is the thing I've been hoping to get my teeth into, but need a good source or good book / paper on piping / chemical engineer level. So far I found a lot of things that just aren't right.
Thanks,
Thomas
I have a problem to solve that seemed trivial at first, but kinda got out of hand quickly. I want to properly calculate pressure drop on a gas pipe on a chemical plant. I thought I'd find "plug and play" equations with iterations maybe, but after 2 days of reading I'm horribly confused.
Can someone point me into a direction of a legit source for compressible flow pressure drop equation? There will be no outlet to atmosphere, no flare - I need to calculate exact value of pressure drop on the line so the equipment downstream from my pipe won't work above design conditions. I did not select the working pressure or design the equipment downstream - all I got is obvious conclusions that I need a certain loss value or things might look bad.
I tried an older version (that is the one available for me) of the 410TP. Simple Darcy equation is easy enough to solve but untrustworhy. Darcy formula including Y factor is infuriating - you need to know the pressure drop in order to calculate Y, so the equation is useless to me.
I did solve a verion of the Isothermal flow equation provided, all good and well, but my spreadsheet is acting funny (probably excel finds it hard to iterate solution since I work with SI units and my pressure is around 40 bar - the equation works for Pa only). I'd like to verify the results. Especially that I suspect it works best for mass flow calculations, if the pressure loss is given.
I found a webpage with free calc, but it gave me an error I'm too dumb to understand (supersonic outflow?). I even went thru the process of learning to use "." instead of "," and the Imperial units for it
I read a lot of sources but most of them I suspect are viable only for natural gas even though they do not state that directly (like Panhandle equation - I always believed it works for natural gas only, but there it was in a paper about gas flow thru pipes).
Gonna go with this one next:
Please help guys - this is the thing I've been hoping to get my teeth into, but need a good source or good book / paper on piping / chemical engineer level. So far I found a lot of things that just aren't right.
Thanks,
Thomas