does anyone have idea or references how to profile tolerance a complex trimmed edge on say a vac formed part? I don't really see any good examples in the standard to other places. Would it make sense to just point to the trimmed edge with a 'ALL OVER' profile tolerance with a note below that states "trimmed edge". using "all around" wouldn't work to me as it is controlled only in the view its shown in and a trimmed edge would go all around in 3d.
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
profile on trimmed edge 8
- Thread starter DGN1975
- Start date
- Status
- Not open for further replies.
Burunduk
Mechanical
- May 2, 2019
- 2,574
Your assignment was to understand what I said about this very same thing at 2 Oct 23 20:19 and 2 Oct 23 21:15. If you didn't get it, you could have asked. You shouldn't have repeated the same complaint.
Your new assignment is to figure out at least one way to derive a set of 3 planes to create a DRF origin from the version that I showed, where the surface does not converge into one point. If you need assistance, ask. Here is a clue - a complex surface which is used as a primary datum feature, will rarely result in the exact same "axis, point, center plane" datum as shown in the standard, so don't be locked in that.
You can use this to get inspiration:
 l
l
Your new assignment is to figure out at least one way to derive a set of 3 planes to create a DRF origin from the version that I showed, where the surface does not converge into one point. If you need assistance, ask. Here is a clue - a complex surface which is used as a primary datum feature, will rarely result in the exact same "axis, point, center plane" datum as shown in the standard, so don't be locked in that.
You can use this to get inspiration:

Here's a variation that locks 6 degrees of freedom - the top and bottom surfaces aren't necessarily parallel to each other or normal to the axis. The axis is arbitrarily oriented relative to the 3 main faces. It does not appear to fit within the suggested possible feature types in ASME Y14.5-2009, figure 4-3.

Your new assignment is to figure out at least one way to derive a set of 3 planes to create a DRF from the version that I showed.

Your new assignment is to figure out at least one way to derive a set of 3 planes to create a DRF from the version that I showed.
Burunduk
Mechanical
- May 2, 2019
- 2,574
Why didn't you do your assignment first?
Fine, I'll tell you one method, but you will have to figure out a different way for your assignment, otherwise it's cheating.
First step is to define the basic relationship between the 3 planar surfaces forming the datum feature. I can place a coordinate system in a random location outside the part, and define each theoretical plane by 3 points that have tabulated coordinates in said coordinate system.
Second step is to limit the form and mutual orientation deviations of the actual surfaces based on the common true profile that was just defined for this group of features. A surface profile feature control frame that applies 3X and has leaders to the surfaces would specify a tolerance with no datum references.
Third step is to label the group of features as a datum feature. The way this is done will affect the datum establishment later. A practical way could be selecting one point on each surface (possibly from the same points already mentioned) and designate them as datum targets such as A1, A2, and A3 - if that is functionally appropriate. The datum simulation device would have to contact the part at these 3 locations. Alternatively, and to stay as close as possible to figure 7-3 (g) which was the original topic, one could attach the datum feature symbol to the profile feature control frame which controls the 3 surfaces. In this case, the datum feature simulator would have the exact shape of the basically defined group of 3 planar surfaces.
Fourth step - deriving the DRF. The three orthogonal datum planes can be established by the same coordinate system that was used to basically define the datum feature.
(Fifth step - controlling the rest of the features on the part - the DRF that was established above will be the origin for the tolerance zones for the other two faces. They will be controlled for profile relative to the datum feature described above.)
Now do your assignment and use a different method.
Fine, I'll tell you one method, but you will have to figure out a different way for your assignment, otherwise it's cheating.
First step is to define the basic relationship between the 3 planar surfaces forming the datum feature. I can place a coordinate system in a random location outside the part, and define each theoretical plane by 3 points that have tabulated coordinates in said coordinate system.
Second step is to limit the form and mutual orientation deviations of the actual surfaces based on the common true profile that was just defined for this group of features. A surface profile feature control frame that applies 3X and has leaders to the surfaces would specify a tolerance with no datum references.
Third step is to label the group of features as a datum feature. The way this is done will affect the datum establishment later. A practical way could be selecting one point on each surface (possibly from the same points already mentioned) and designate them as datum targets such as A1, A2, and A3 - if that is functionally appropriate. The datum simulation device would have to contact the part at these 3 locations. Alternatively, and to stay as close as possible to figure 7-3 (g) which was the original topic, one could attach the datum feature symbol to the profile feature control frame which controls the 3 surfaces. In this case, the datum feature simulator would have the exact shape of the basically defined group of 3 planar surfaces.
Fourth step - deriving the DRF. The three orthogonal datum planes can be established by the same coordinate system that was used to basically define the datum feature.
(Fifth step - controlling the rest of the features on the part - the DRF that was established above will be the origin for the tolerance zones for the other two faces. They will be controlled for profile relative to the datum feature described above.)
Now do your assignment and use a different method.
Sorry, only intrinsic answers allowed, as shown in Figure 7-4.
None of the Figure 7-3 examples include a dimensioning scheme or pre-defined CSYS as a framework to derive the constraints.
You can use only the geometry as presented and not create separate coordinate systems to justify a DRF that uses the coordinate system. That is called "begging the question."
Suppose the feature is defined by mutual basic dihedral angles and edge lengths. Your method doesn't work as no CSYS is required.
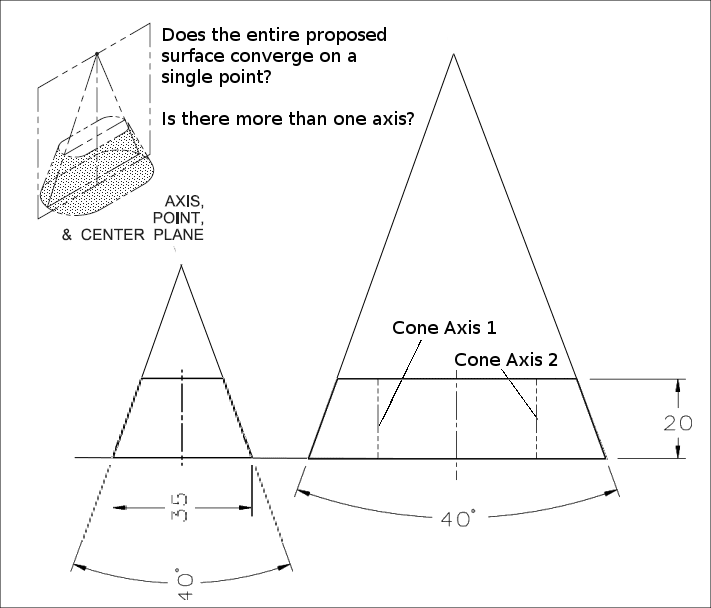
Your previous (g) attempt fails as it contains two intrinsic axes from the semi-conical ends and one axis from the flat face tangent planes intersecting and two points from the intersections of the first two axes; there is an additional axis from the tangent planes to the cones that does not intersect any of the other axes or points. This was not reducible per (g) to a single point and rotation constraints and does not form a single point+orientation control.
No amount of alteration will bring all the axes to a single point.
Whatever you expect of me is in such random terms without a clear goal as to be nonsensical. The discussion is that the standard's model shown for (g) has not got the properties shown in the remaining parts of the figure no matter how much you wish it had.
The creators of the chart used symmetry planes to establish datum planes; ironic they eliminated symmetry controls. Where is the center axis in a rhombus section linear extrusion? Or for a pattern of holes? About which axis will the pattern be centered if there is no intrinsic symmetry?
None of the Figure 7-3 examples include a dimensioning scheme or pre-defined CSYS as a framework to derive the constraints.
You can use only the geometry as presented and not create separate coordinate systems to justify a DRF that uses the coordinate system. That is called "begging the question."
Suppose the feature is defined by mutual basic dihedral angles and edge lengths. Your method doesn't work as no CSYS is required.
Your previous (g) attempt fails as it contains two intrinsic axes from the semi-conical ends and one axis from the flat face tangent planes intersecting and two points from the intersections of the first two axes; there is an additional axis from the tangent planes to the cones that does not intersect any of the other axes or points. This was not reducible per (g) to a single point and rotation constraints and does not form a single point+orientation control.
No amount of alteration will bring all the axes to a single point.
Whatever you expect of me is in such random terms without a clear goal as to be nonsensical. The discussion is that the standard's model shown for (g) has not got the properties shown in the remaining parts of the figure no matter how much you wish it had.
The creators of the chart used symmetry planes to establish datum planes; ironic they eliminated symmetry controls. Where is the center axis in a rhombus section linear extrusion? Or for a pattern of holes? About which axis will the pattern be centered if there is no intrinsic symmetry?
Burunduk
Mechanical
- May 2, 2019
- 2,574
I see that the inspiration aid didn't help.
There will be a CSYS anyway as long as you establish a DRF. A theoretic DRF is made of 3 perpendicular planes and 3 perpendicular axes (with no defined positive and negative directions) that establish an origin for measurements. At practice a CSYS that is tied to the datum simulators is eventually used to represent a DRF and define that origin. There are many possibilities for basically dimensioning the datum feature. Choosing one dimensioning possibility over the other doesn't affect the ability to establish the DRF this way or that way.
The 7-3 is made of specific examples and does not cover all possible realistic cases, or everything that is "allowed". As you have seen, with a slight modification of the shape and proportions for (g) you do not get the exact same datum. Regardless, one could still establish 3 planes and an origin based only on the intrinsic geometry for my version of the shape. It just doesn't have to be a "plane, axis, point" datum in that exact combination and method of derivation. A datum can be a point, a line, an axis, a plane, or any combination of them. There are countless possible combinations of these elements that can be associated with different feature geometries or groups of features. Any datum can be used to base a DRF on, not just the "plane, axis, point" set.
Your assignment was to figure out a way to construct a DRF based on the shape and dimensions I suggested as a unique version of the (g) complex feature, not by copy-pasting from the 7-3 chart. So far, you haven't succeeded. Give it some more attempts, it is the only way to learn.
3D said:Suppose the feature is defined by mutual basic dihedral angles and edge lengths. Your method doesn't work as no CSYS is required.
There will be a CSYS anyway as long as you establish a DRF. A theoretic DRF is made of 3 perpendicular planes and 3 perpendicular axes (with no defined positive and negative directions) that establish an origin for measurements. At practice a CSYS that is tied to the datum simulators is eventually used to represent a DRF and define that origin. There are many possibilities for basically dimensioning the datum feature. Choosing one dimensioning possibility over the other doesn't affect the ability to establish the DRF this way or that way.
3D said:Sorry, only intrinsic answers allowed
The 7-3 is made of specific examples and does not cover all possible realistic cases, or everything that is "allowed". As you have seen, with a slight modification of the shape and proportions for (g) you do not get the exact same datum. Regardless, one could still establish 3 planes and an origin based only on the intrinsic geometry for my version of the shape. It just doesn't have to be a "plane, axis, point" datum in that exact combination and method of derivation. A datum can be a point, a line, an axis, a plane, or any combination of them. There are countless possible combinations of these elements that can be associated with different feature geometries or groups of features. Any datum can be used to base a DRF on, not just the "plane, axis, point" set.
Your assignment was to figure out a way to construct a DRF based on the shape and dimensions I suggested as a unique version of the (g) complex feature, not by copy-pasting from the 7-3 chart. So far, you haven't succeeded. Give it some more attempts, it is the only way to learn.
You began by forcing a CSYS to define my feature - not required and does not fit the figure. Your method does not apply to either my example or any of Figure 7.4. My example was to show no such fit was possible and the figure showed no way to manage it.
"Regardless, one could still establish 3 planes and an origin based only on the intrinsic geometry for my version of the shape."
Your shape includes multiple possible DRFs - the task was to create a shape with one, as desired and not accomplished by (g) geometry.
"Regardless, one could still establish 3 planes and an origin based only on the intrinsic geometry for my version of the shape."
Your shape includes multiple possible DRFs - the task was to create a shape with one, as desired and not accomplished by (g) geometry.
Burunduk
Mechanical
- May 2, 2019
- 2,574
Any shape without exception can result in multiple possible DRFs. For the simple cases such as 7-4 there are simple and obvious defaults. However, there are no consequences of overriding those defaults as long as the spatial relationship between the DRF and the datum-simulators/TGCs is kept fixed. For a bit less trivial cases, such as figure 7-60, you have to make an arbitrary choice between more than one equally good options for the location of the DRF. For more complicated cases, there are no defaults at all.
7-3 (g) showed one possible special case geometry with one possible datum solution.
There was no reason not to apply a CSYS based solution for your example, although there are other options too.
7-3 (g) showed one possible special case geometry with one possible datum solution.
There was no reason not to apply a CSYS based solution for your example, although there are other options too.
You still don't see how 7-3(g) is defective? To get what the interpretation shows all tangent planes must pass through the same point. The model in the figure doesn't resolve to one point, a failure you duplicated without understanding the problem. It was part of a series showing geometry with only one solution, but it didn't show the geometry required to do so in (g).
Burunduk
Mechanical
- May 2, 2019
- 2,574
"To get what the interpretation shows all tangent planes must pass through the same point."
There is no way of knowing for sure that the figure attempts to show what you think it does. That may be entirely your idea.
It is not a cone and there is no reason for it to converge into a single apex point.
I see a bisecting plane based on the flat taper and two lines created from the intersection of that plane with the semi-cones. The two lines meet at a point from which an axis that lies on the plane and bisects the angle between the two lines originates. As I explained, all this matters very little - they could have shown a solution with a completely different structure of a datum even for the exact same shape.
There is no way of knowing for sure that the figure attempts to show what you think it does. That may be entirely your idea.
It is not a cone and there is no reason for it to converge into a single apex point.
I see a bisecting plane based on the flat taper and two lines created from the intersection of that plane with the semi-cones. The two lines meet at a point from which an axis that lies on the plane and bisects the angle between the two lines originates. As I explained, all this matters very little - they could have shown a solution with a completely different structure of a datum even for the exact same shape.
Or, it may be the original intention as the solution in the standard shows and the artwork was done by someone who failed to understand how to do so.
From your position they might as well have used a scribble as the original and drawn anything as the interpretation.
Congrats on realizing it is not a cone; it still remains that a non-cone can have a single apex yet also control all degrees of rotation as is the expected interpretation.
From your position they might as well have used a scribble as the original and drawn anything as the interpretation.
Congrats on realizing it is not a cone; it still remains that a non-cone can have a single apex yet also control all degrees of rotation as is the expected interpretation.
The entire surface is shown related to the point. They show a trimetric that matches my interpretation that doesn't match the orthographic or yours.
Occam's razor, adapted - the simpler geometry is the right one. The drafter screwed up and you never noticed the clear error.
Occam's razor, adapted - the simpler geometry is the right one. The drafter screwed up and you never noticed the clear error.
Burunduk
Mechanical
- May 2, 2019
- 2,574
In the trimetric they do not show the extrapolation of the flat taper surfaces, so it is not indicated that they are supposed to converge into the point shown. The trimetric shows exactly what I described.3D said:They show a trimetric that matches my interpretation
To apply Occam's razor logic is to look for the simpler explanation. The simpler explanation takes the figure and related text just for what they show and say, no more and no less. It does not assume an intent that was not met or an error.
- Thread starter
- #58
OMG LOL. I didn't check this thread for a few days to come back to this.... Thanks guys lol!!!!. I'm new to eng-tips, but thanks for the entertainment.
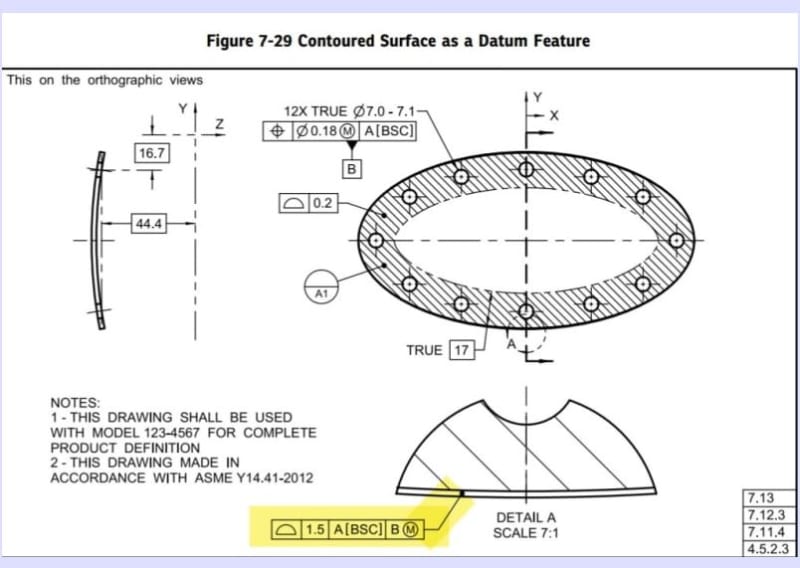
Burunduk, Now going back to one post of yours from Sept 30 where you had a screen shot of the 2018 standard (I only have the 2009 standard) I noticed a descrenacy between the standards.
My 2009 standard had the "all around" symbol on it and the 2018 version you showed does not, so they must of tried to clear some issues up???
I have always understood all around as having to be used in one view where the surface was perpendicular to the view. I hadn't studied this figure closely, but seeing the all around sym in 2009 confuses me more.
is that why they removed it in 2018?
2018???
2009
Burunduk, Now going back to one post of yours from Sept 30 where you had a screen shot of the 2018 standard (I only have the 2009 standard) I noticed a descrenacy between the standards.
My 2009 standard had the "all around" symbol on it and the 2018 version you showed does not, so they must of tried to clear some issues up???
I have always understood all around as having to be used in one view where the surface was perpendicular to the view. I hadn't studied this figure closely, but seeing the all around sym in 2009 confuses me more.
is that why they removed it in 2018?
2018???

2009

DGN1975,
That surface is without sharp discontinuity so the ALL AROUND would not be required. Since no profile of the surface is shown it is necessary to add the note and supply the model of your part to manufacturing and QA.
That ALL AROUND was previously used is because 2009 was a rush job and, I presume, that the Y14.41 was updated since then and so they copy/pasted the new, correct diagram.
That surface is without sharp discontinuity so the ALL AROUND would not be required. Since no profile of the surface is shown it is necessary to add the note and supply the model of your part to manufacturing and QA.
That ALL AROUND was previously used is because 2009 was a rush job and, I presume, that the Y14.41 was updated since then and so they copy/pasted the new, correct diagram.
- Status
- Not open for further replies.
Similar threads
- Replies
- 6
- Views
- 3K
- Locked
- Question
- Replies
- 21
- Views
- 10K
- Replies
- 31
- Views
- 7K
- Locked
- Question
- Replies
- 24
- Views
- 4K
- Locked
- Question
- Replies
- 15
- Views
- 4K