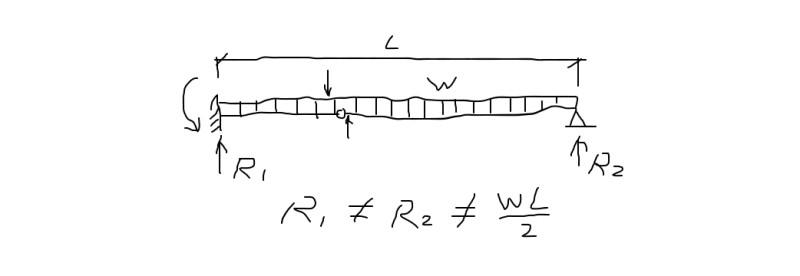rifa92
Mechanical
- Apr 17, 2020
- 30
Hi,
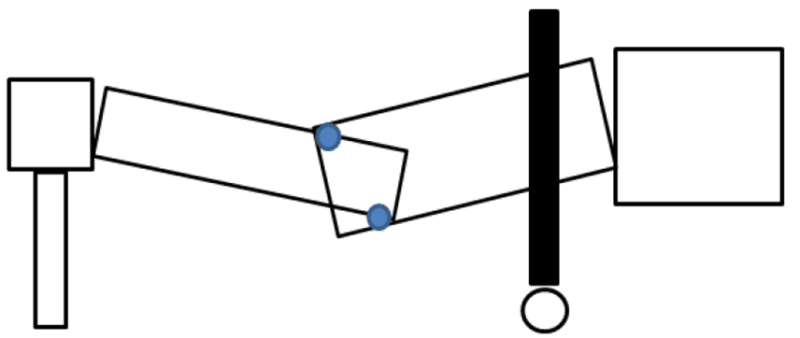
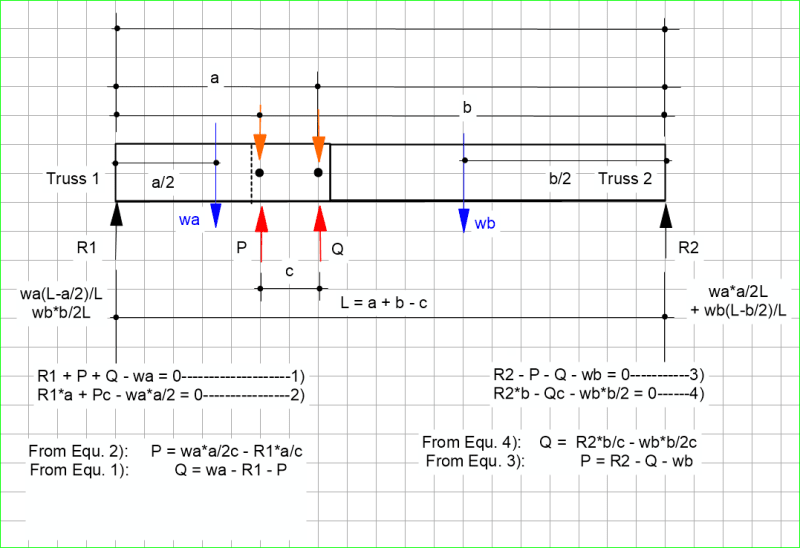
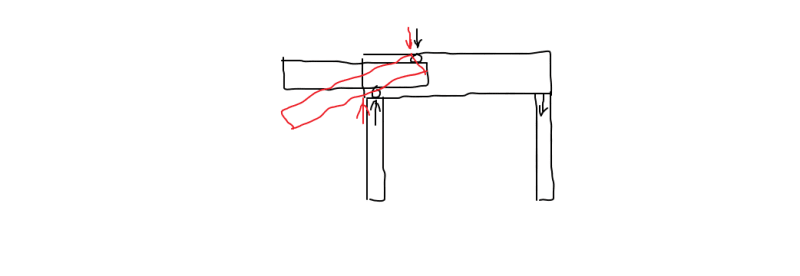
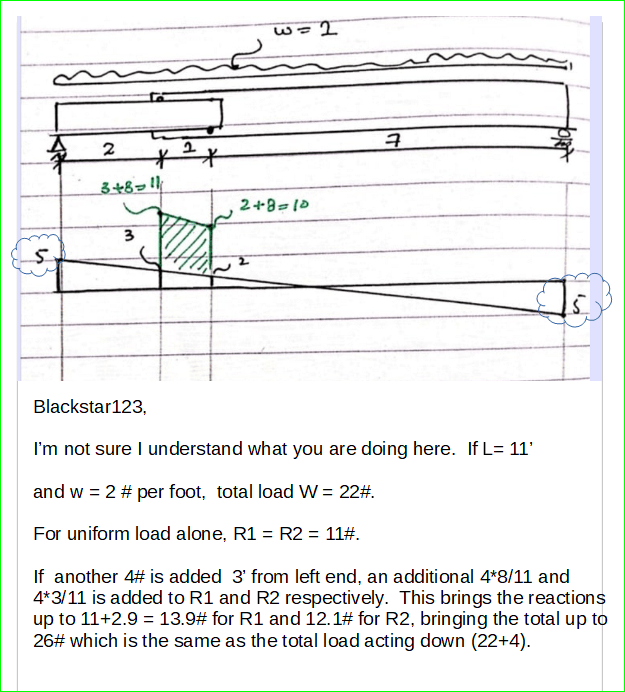
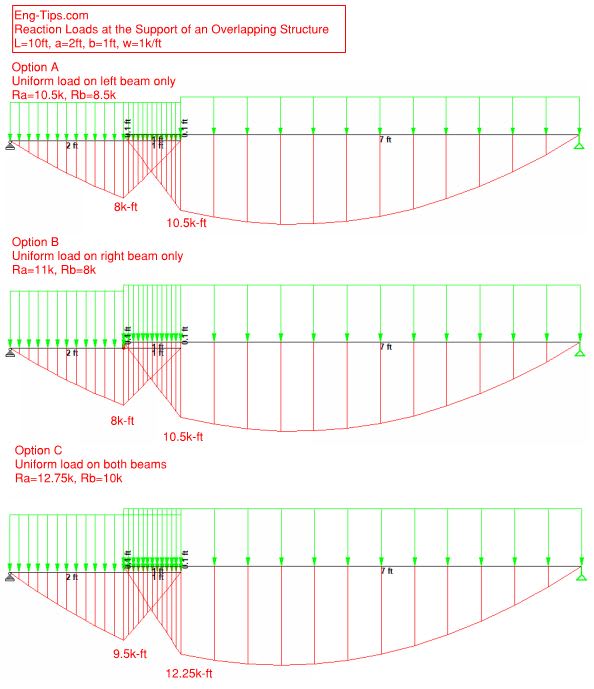
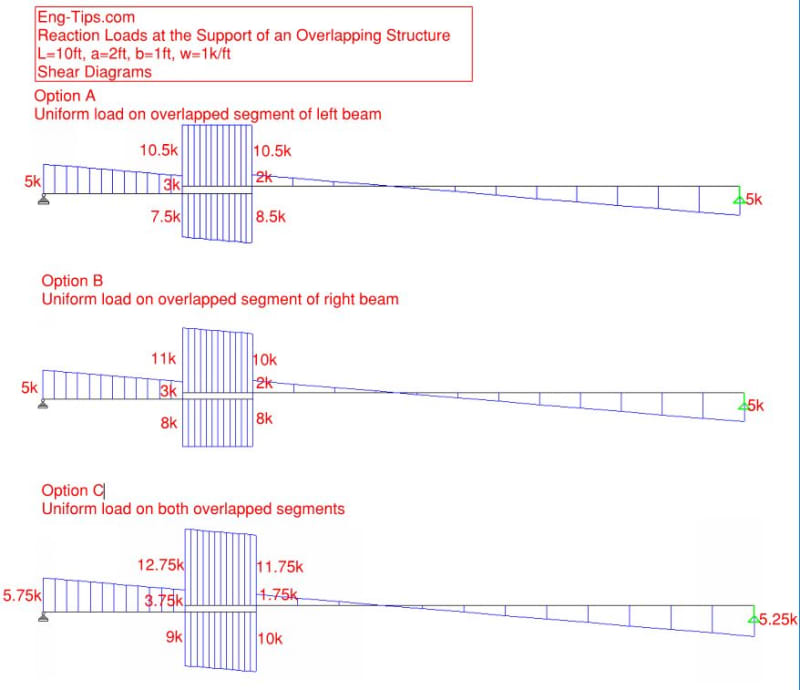
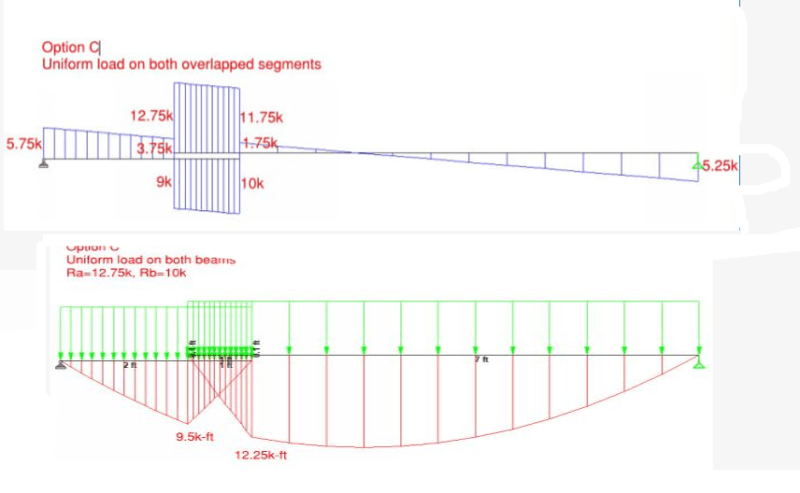
I wanted some clarification for how would the reaction loads at end supports and joint will be calculated in the case shown in the schematic diagram. The load of right structure would be supported by roller A however that load would also be transmitted to roller B. In this for value we can just assume that the uniform distributed load of the structure is 30 kg/m2 and distance horizontal distance between rollers is 1m. Thanks in advance.
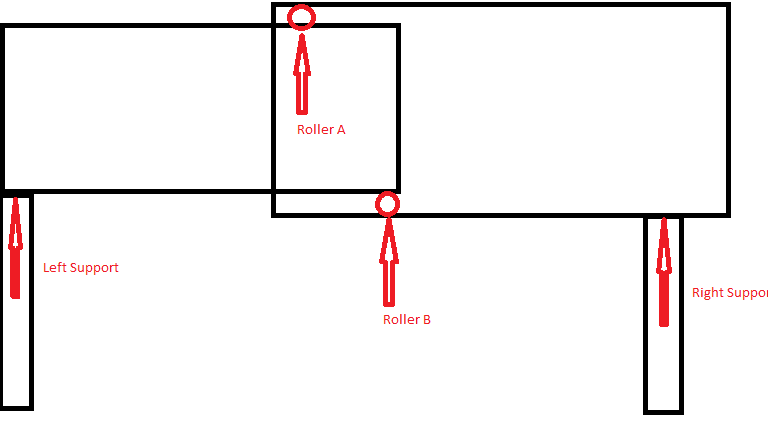
I wanted some clarification for how would the reaction loads at end supports and joint will be calculated in the case shown in the schematic diagram. The load of right structure would be supported by roller A however that load would also be transmitted to roller B. In this for value we can just assume that the uniform distributed load of the structure is 30 kg/m2 and distance horizontal distance between rollers is 1m. Thanks in advance.