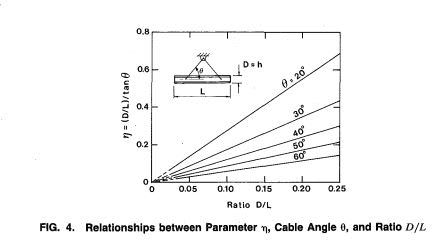
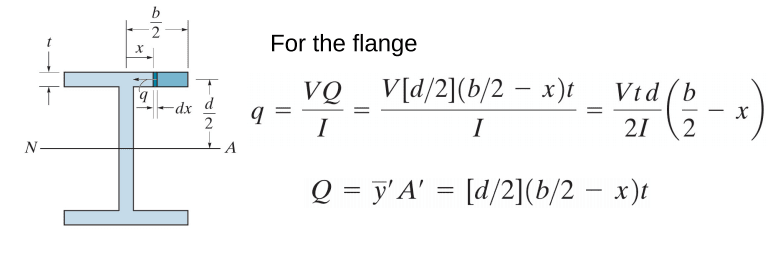JP20
Structural
- Apr 7, 2020
- 41
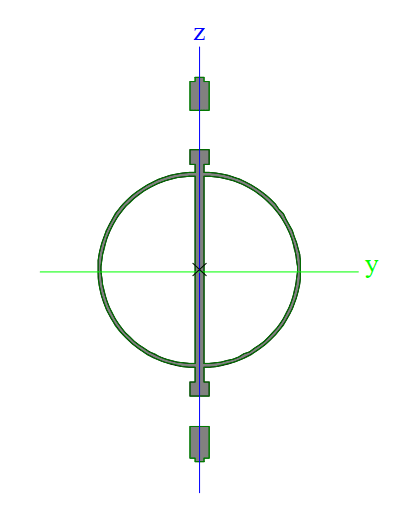
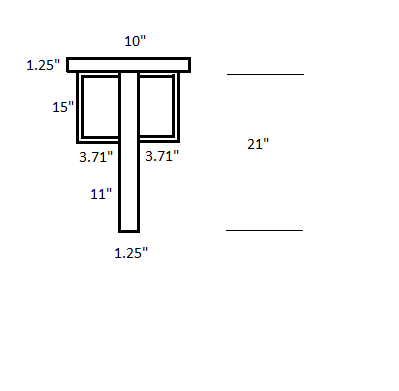
I have the below scenario: How do I resolve the force being applied to the welds given a max shear and a max moment (developed from shear-moment diagram).
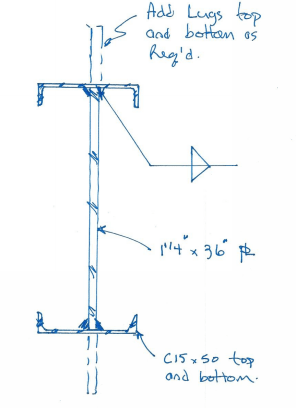
The orange dots represent locations of the fillet welds. Channels are 15" deep. plate is 36" deep.
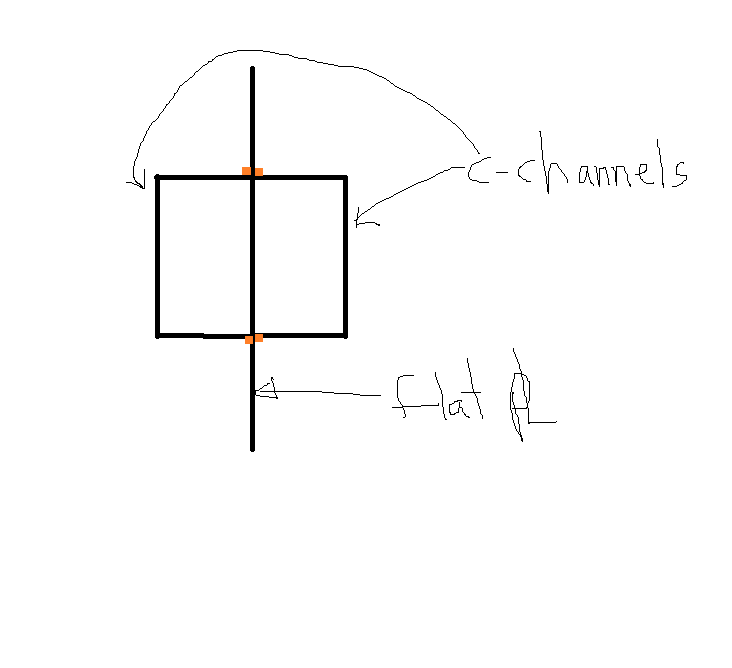
The orange dots represent locations of the fillet welds. Channels are 15" deep. plate is 36" deep.