Welding on a Beam 2

[JP20]

I have the below scenario: How do I resolve the force being applied to the welds given a max shear and a max moment (developed from shear-moment diagram).
The orange dots represent locations of the fillet welds. Channels are 15" deep. plate is 36" deep.

 

[KootK]

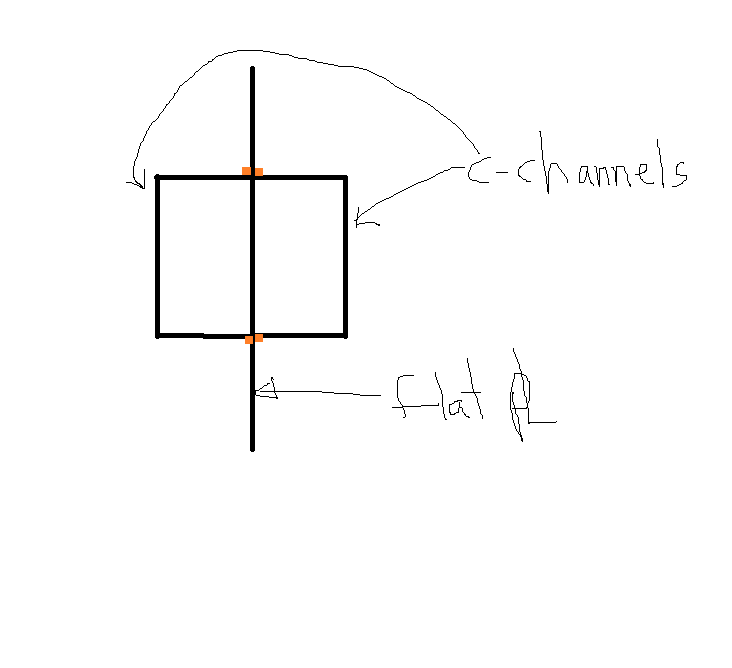
Thanks. Let me throw this out there... thinking about changing the section to the following so the compression will, without a doubt, be transferred to a wide flange:

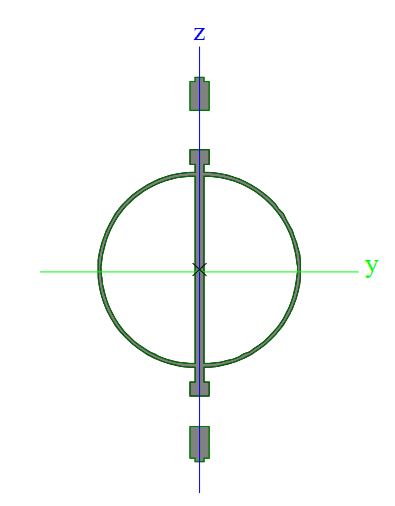
I would give some serious consideration to something like Craig's recommendation, repeated below. Not that it necessarily has to be ac circular section etc.

While it may not optimize your material costs to the nuts, one very simple way to shed the complexity involved with this stuff is to design yourself a cross section that would work for both strength and stiffness even if it did roll over in lateral torsional buckling. Flip the thing sideways and make it work that way as a beam column.
Obviously, that makes for a section with a lot of weak axis meat to it. But, then, you've got a fairly simple and reliable solution that you can execute without too much fuss.

One problem with your current section is that, with your three point support condition, sometimes the compression flange will be the bottom flange. In that case, you'll have your edge stiffening on the wrong side.

 

[CANPRO]

KootK, at the risk of being labelled difficult, I'm going to be disagreeable in this thread again. I know you can handle some disagreement and healthy debate, so here we go:

Both of the references you listed are for I-beams, and every reference I've seen for LTB buckling checks are for an I-section or at least something with a distinct compression flange. With the section proposed by Craig and re-posted by you, what would you consider to be effective compression flange? A portion of the round member near the top? I think it is important to have a compression flange with some healthy Iy properties near to the extreme compression fiber and I don't think you get that here - and I believe this is the basis of the references you've presented. If you took a standard I section, kept the same overall depth, and moved the compression flange down 20% of the beam depth you surely wouldn't get the same LTB resistance out of the flange. And to me this makes sense - any time LTB comes up here you drive home the point that the beam has to deflect sideways and rotate about a point in space. If you lower your compression flange, it gets closer to the point of rotation and becomes less effective in resisting this rotation. This is why I proposed using the channels as an I-section.

 

[KootK]

Both of the references you listed are for I-beams

Yup, but I would argue that:

1) The general principles still largely apply and are worth knowing about and;

2) Depending on the direction OP takes, treating his real cross section as an equivalent wide flange might prove attractive.

With the section proposed by Craig and re-posted by you, what would you consider to be effective compression flange? A portion of the round member near the top?

That's what I had in mind, yes.

I think it is important to have a compression flange with some healthy Iy properties near to the extreme compression fiber and I don't think you get that here .

The approach that I recommended would treat the flat plate as entirely sacrificial except for local transfer of loads in and out of the system. As such, I've little concern for the Iy properties near the extreme compression fiber.

That said, I voiced a similar concern in OP's previous thread on this topic.

..your critical failure mode is likely to be out of plane plate buckling of the portions of the flat plate extended above and below the channels.

If the design assumes that the plate is to be fully utilized in flexure, I imagine that one would check this failure mode via b/t ratios or something similar. With plate extensions 1.25" thick and 8"+/- long, I don't see this being much of a problem.

 

[r13]

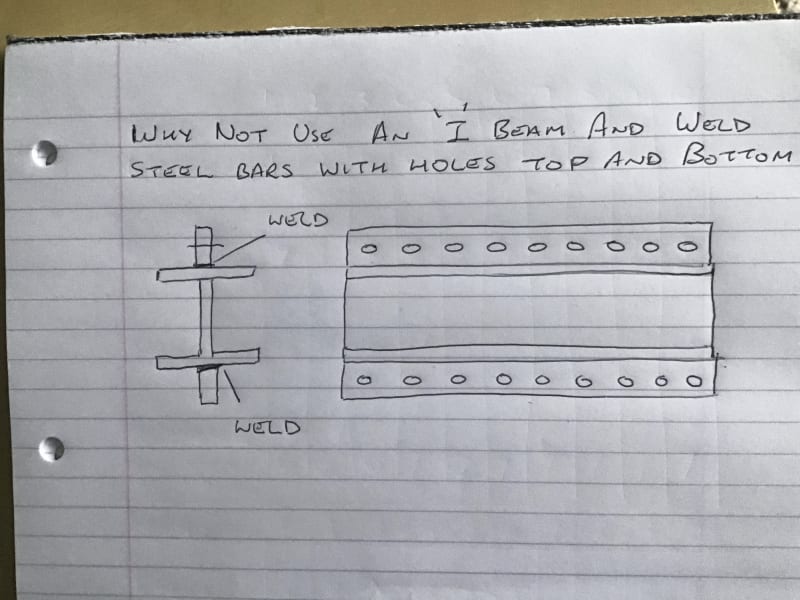
I agree the latest solution by CANPRO is more functional/desirable, but then why not use a standard WF, or I, as suggested way back to the beginning of this thread!?

By the way, johns20188 has opened a thread devoted to the discussion of designing this type of built-up members. For interested parties, please jump in and provide your opinions, and not to side track the JP20's attention.

 

[desertfox]

My thoughts from the file uploaded earlier

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[BAretired]

Getting back to the original question, at ultimate load, each channel is stressed to Fy, compression tension on top, tension compression on the bottom. The total force in the top and bottom of the channel is Fy*A/2. That has to be developed by a weld of length L/2. If we assume uniform distribution from end to centre, the weld must carry a force per unit length of Fy*A/L where A is the area of channel and L is the span of the built-up section.

BA

 

[CANPRO]

Getting back to the original question, at ultimate load, each channel is stressed to Fy, compression tension on top, tension compression on the bottom. The total force in the top and bottom of the channel is Fy*A/2. That has to be developed by a weld of length L/2. If we assume uniform distribution from end to centre, the weld must carry a force per unit length of Fy*A/L where A is the area of channel and L is the span of the built-up section.

I disagree with a couple parts of this statement. First, if you look at the proportions of this beam, there is no chance that the channel flanges get to see Fy before this fails - the beam is far too flimsy to reach yield before buckling.

Further, it has been thoroughly discussed here that the development of bending stress in the channel flanges does not come from the welds - centroids of all sections align, Q = 0, no shear flow in the welds. Any bending stress developed in the flanges of these channels would come from shear flow between channel web and flange.

Kootk, I get what you were suggesting now - the bit of plate above the circular section is essentially just a continuous lug. I'd be comfortable using that bit of plate for checking the cross-section strength (healthy b/t ratio as you suggest), but for LTB checks I would assume that bit of plate doesn't exist and that top of beam = top of circular section.

 

[r13]

BA's method is the practical method of design, the stresses create a couple on the channels, and force the channels to separate from the center plate, thus require weld to glue the pieces together.

 

[BAretired]

I disagree with a couple parts of this statement. First, if you look at the proportions of this beam, there is no chance that the channel flanges get to see Fy before this fails - the beam is far too flimsy to reach yield before buckling.

Who cares? I don't know how the size of the channel was determined, but the capacity of a section in flexure, built up or otherwise, is developed when everything above and below the N.A. is stressed to Fy, one in compression and one in tension. In order to get the force into the channel, the only connection you've got is the weld to the plate at the top and bottom of the channel.

How long is the beam? Do we know? Check it out. The OP needs answers quickly and you can't do any better than weld to fully develop the channels in bending.



BA

 

[r13]

The beam is 40' long, with 3 slings on top and multiple lift loads below. The channel wasn't sized, but an attempt to prevent buckling.

 

[BAretired]

Well, if the channel size is C380x50 (C15x33.9) and the span is 20'-0" or say 6000mm, the weld must be good for 6430*300/6000 = 320N/mm which would require an intermittent weld of 6mm (not worth getting excited about).

What may be worth getting excited about, however, is the question of buckling. This needs to be properly checked to determine whether or not the proposed section is adequate for the rated capacity of the lifting beam.

BA

 

[CANPRO]

Who cares? I don't know how the size of the channel was determined, but the capacity of a section in flexure, built up or otherwise, is developed when everything above and below the N.A. is stressed to Fy, one in compression and one in tension.

Presumably, whoever is designing the beam would care if the failure mode is by section yield or buckling.

How long is the beam? Do we know? Check it out.

This thread is up to 90 replies now. And it is a continuation of another thread. I'm sorry if I'm being a bit cranky right now, but if you read through the thread you would have seen the section sizes and beam length, and you would have seen the long discussion regarding the load in the welds. BA, I have a lot of respect for you and I've learned a lot from you over the years, I mean this with all due respect.

The total force in the top and bottom of the channel is Fy*A/2. That has to be developed by a weld of length L/2

BA's method is the practical method of design, the stresses create a couple on the channels, and force the channels to separate from the center plate, thus require weld to glue the pieces together

I can't believe I'm still here saying this. The bending stress in the flange of the channel does not come from the weld. This is fundamentally incorrect. The centroids of all components align with the neutral axis of the built-up section, there is no shear flow in the weld. There is no tendency for the interface between the channel and the plate to slip relative to each other in the longitudinal direction. Therefore the weld cannot possibly be responsible for building up bending stress in the channel flange. All of these other methods might sound rational but they are just work-arounds for doing it proper - and the proper way isn't hard! Its a college level shear flow problem. If OP was to build this beam as proposed, there would be some stress in the welds (as has been discussed here and in Johns20188's new thread) but it isn't shear flow.

 

[r13]

CANPRO and BA,

You are invited to the thread opened by johns20188, so more people can join the discussion without browse through and read the lengthy responses.

 

[BAretired]

Three slings creates a problem of indeterminacy which may be okay, but I prefer a determinate system. Two slings, I believe would be better. If the beam is forty feet long, the pickup points would not be at the ends, but say a' from each end leaving a span of b' in the middle. Then 2a+b = 40, so if a = 8, b = 24'. I don't know, but I think that's about right.

Cantilever moment = 8^2/2 = 32w; Span positive moment = 24^2/8 -32 = 40w

Then check for buckling and modify a and b as required. If that doesn't work, beef up the section using whatever material is available on site.

BA

 

[JP20]

I decided to just use a W16x77 with lugs welded on top and bottom flanges in line with the webs. Kl/r for weak axis is 196. However this is a lot of determining factors in BTH manual that I still have to check. I did check welds earlier today and they are good being 8” long on both sides of lug - 1/2” fillet.

This beam is going to be rated for 25 Tons of lifting.

The part I hate most is that no matter what you do to this type of lifting device, you cannot laterally brace it. If someone knows of a way to, let me know! Otherwise I’ll be using BTH manual to design as 40’ unbraced.

 

[KootK]

I'm with CANPRO et al on:

1) The shear flow theory that applies (or doesn't apply) here and;

2) the value of a correct theoretical understanding even if a gross, overkill approach would do.

I'll tell my story the the long way let folks pick and choose which bits they might light to challenge.

THE TWO COMPONENTS OF COMPOSITE FLEXURAL FASTENING

3) All components of the cross section must be induced, by the fastening, to assume the same curvature along their independent axes. This is usually the low demand aspect of fastening demand.

4) Where the joining of the components would increase the moment of inertia of the assembly above the sum of the separate components, the fastening must also axially extend and axially compress the component parts uniformly. This is usually the high demand part of the fastening demand as outright elongating or shortening a piece of steel really takes some doing.

THE SPECIAL CASE OF ALL COMPONENT NEUTRAL AXES BEING COINCIDENT

When this is the case, #4 is unnecessary and #3 is all that applies with respect to the fastening. This should make intuitive sense because, really, if your moment of inertia isn't going to get pushed any higher than SUM(Ix_components), why should you have to pump a ton of capacity into making that happen? You shouldn't, of course.

HOW TO FASTEN WHEN THE COMPONENT CENTROIDS ARE COINCIDENT?

It doesn't take much really. And there are two options. In step by step fashion:

1) Based on the ratio Ix_component / Ix_assembly, figure out how much load goes into each competent part. This will create a condition wherein all component parts have the same centroidal curvatures along their lengths and share a common cross section strain profile (this last bit is really what the crux of composite flexural action is).

2) Having determined the load on each component, the shear and moment diagrams for those components become determinate. They are what they are and they need to be internally consistent.

3) The problem now becomes one of imposing the requisite shear and moment diagrams from #2 on the component being fastened given that it may be that no external load is applied to the component. There are two fundamental approaches:

a) Transfer increments of shear from the assembly to the component to replicate the shear diagram that the component should have. This will result in the desired moment diagram falling into place. In this case, the welds would be designed for vertical loads only of a magnitude equal to the distributed load going to the component divided by two, applied top and bottom. This is often how we do it in wood and the fastening demand is very light except, sometimes, at reaction points, cutoffs etc where large amounts of concentrated load must be moved in or out of the component locally.

b) Transfer increments of moment from the assembly to the component to component to replicate the moment diagram that the component should have. This will result in the desired shear diagram falling into place. In this case, the top and bottom weld lines would be designed for horizontal loads only of a magnitude equal to [V/h], varying along the length of the beam [V = shear; h = distance between weld lines]. This is the method that I would favor for this application given that the path for vertical shear transfer is made a bit flexible as a result of it needing to pass through the channel flanges and induce transverse bending there.

One or the other of 3a or 3b will usually make more sense than the other based on the connection style etc. Where it's not obvious, I'll design for the worst of both cases. It's usually a pittance either way.

One could certainly be forgiven for getting the impression that #3a and #3b are both versions of "shear flow" (especially #3b). Both methods do move load around via weld shear after all. For me, the difference is that neither method attempts to impose a uniform axial strain on a component of the section which I take to be the thing that defines a classic "shear flow" problem. I suppose that another way to look at it is to say that the coincident centroids case is really just a special case of the shear flow problem in which it is possible, but not necessary, to transfer load into the component members via horizontal shear.

 

[KootK]

The part I hate most is that no matter what you do to this type of lifting device, you cannot laterally brace it. If someone knows of a way to, let me know!

Whatever would you be bracing the beam to? It will be floating around arbitrarily in space. At best, you can "brace" the slender parts of your compressed elements to attached, less slender parts. A better term for that is probably stiffening rather than bracing though.

 

[BAretired]

This thread is up to 90 replies now. And it is a continuation of another thread. I'm sorry if I'm being a bit cranky right now, but if you read through the thread you would have seen the section sizes and beam length, and you would have seen the long discussion regarding the load in the welds. BA, I have a lot of respect for you and I've learned a lot from you over the years, I mean this with all due respect.

I apologize for joining the discussion so late. It is true, I didn't read through the thread and again, I apologize for that. Thank you for the compliment and I can say that I have a lot of respect for your contributions to this forum.

EDIT: Please ignore all the red notations. CANPRO is absolutely correct.

I can't believe I'm still here saying this. Neither can I.

The bending stress in the flange of the channel does not come from the weld.
It really does. Without the weld, the channel would feel no bending stress while the plate would elongate or shorten at the elevation of the top and bottom of the channel.

This is fundamentally incorrect. The centroids of all components align with the neutral axis of the built-up section, there is no shear flow in the weld. There is no tendency for the interface between the channel and the plate to slip relative to each other in the longitudinal direction. Therefore the weld cannot possibly be responsible for building up bending stress in the channel flange. There is no other way to get flexural stress into the channels.

All of these other methods might sound rational but they are just work-arounds for doing it proper - and the proper way isn't hard! Its a college level shear flow problem. If OP was to build this beam as proposed, there would be some stress in the welds (as has been discussed here and in Johns20188's new thread) but it isn't shear flow.

I believe it is, but I think we are both repeating ourselves.

CANPRO is correct. Please ignore my comments in red.


BA

 

[BAretired]

I decided to just use a W16x77 with lugs welded on top and bottom flanges in line with the webs. Kl/r for weak axis is 196. However this is a lot of determining factors in BTH manual that I still have to check. I did check welds earlier today and they are good being 8” long on both sides of lug - 1/2” fillet.

This beam is going to be rated for 25 Tons of lifting.

The part I hate most is that no matter what you do to this type of lifting device, you cannot laterally brace it. If someone knows of a way to, let me know! Otherwise I’ll be using BTH manual to design as 40’ unbraced.

Using a WF is definitely a good idea.
I believe you should use only two slings, not three.
I believe you should pick up substantially closer than 40' (possibly 8', 24', 8').
It's not possible to brace it, but the beam must be capable of handling the compression for an unsupported length of 24' (or whatever central span you decide upon).

BA

 

[CANPRO]

BA, well then with no hard feelings, let the debate continue. Although this might be better served for the other thread. But to quickly answer back to your statement "It really does. Without the weld, the channel would feel no bending stress" - the bending stress in the channel flange would result from shear flow between the web of the channel and the flange. The channel and plate could be joined at the neutral axis only and you'd still get the same bending stress in the channel - as the plate deforms, the channel is forced to deform with it and the load is shared in proportion to the bending stiffness, and bending stress still develops in the channel flange due to shear flow between the web and flange.