Burunduk
Mechanical
- May 2, 2019
- 2,513
During a recent discussion that developed in thread1103-501700 , claims were made that at every place where the Translation Modifier is used, the Customized Datum Reference Frame tool can be used instead.
Here is an excerpt of the argumentation:
Other opinions that were expressed suggested otherwise:
I'm interested in clarifying the issue.
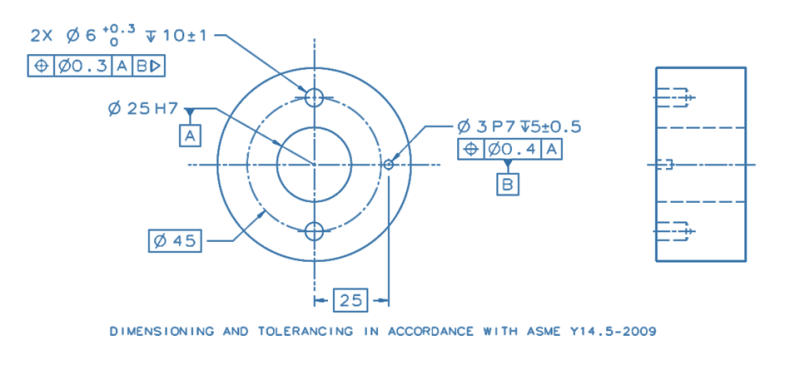
Below is a drawing example that uses the Translation Modifier tool.
The ⌀25H7 bore is the locating feature of this component in its functional assembly, and it also sets its initial orientation. It aligns to a mating shaft with a "sliding" clearance fit of H7/g6 (hole basis). The ⌀3P7 hole is intended to fit with a pin that will be assembled into it with an Interference fit of P7/h6 (shaft basis). The pin will contact a radial slot on the mating part to lock the rotation about the axis of the bore, to do the "clocking".
If you were to duplicate the effect of the Translation Modifier applied to datum feature B by using a Customized DRF, how would you go about it? What would the customized datum reference frame look like, and how would it override the default degrees of freedom constrained by datum features A primary, B secondary?
If you think this idea would not work and the translation modifier should be kept, please explain why.
I would appreciate everyone's opinions.
Thank you.
Here is an excerpt of the argumentation:
3DDave said:The point is that customized datum reference frames are a proper superset of which the translation modifier is a tiny part. That there is no function available via the translation modifier that is not contained within the customized datum reference frame capability. That the control of acceptable variation by the more capable approach is identical to the more limited approach with the correct syntax.
Other opinions that were expressed suggested otherwise:
Evan said:In some cases (such as the plane-hole-slot case discussed earlier in the thread) the same DRF can be achieved using either tool but this is not true in the majority of cases.
I'm interested in clarifying the issue.
Below is a drawing example that uses the Translation Modifier tool.
The ⌀25H7 bore is the locating feature of this component in its functional assembly, and it also sets its initial orientation. It aligns to a mating shaft with a "sliding" clearance fit of H7/g6 (hole basis). The ⌀3P7 hole is intended to fit with a pin that will be assembled into it with an Interference fit of P7/h6 (shaft basis). The pin will contact a radial slot on the mating part to lock the rotation about the axis of the bore, to do the "clocking".
If you were to duplicate the effect of the Translation Modifier applied to datum feature B by using a Customized DRF, how would you go about it? What would the customized datum reference frame look like, and how would it override the default degrees of freedom constrained by datum features A primary, B secondary?
If you think this idea would not work and the translation modifier should be kept, please explain why.
I would appreciate everyone's opinions.
Thank you.

