Rafter without fly brace? 22

[fourpm]

I am designing rafters to AS4100 and wondering what if I don't use fly brace. I understand that with fly brace it will give you full restraint. But if I don't use fly brace, will the purlin above be considered as lateral restraint for rafter under uplift? If so. can I take the purlin spacing as segment and the only factor that changes without fly brace is kt?
I have the same question when it comes the continuous steel floor beam design where Z/C floor joints sit on top of the beam. What segment should I take for the beam near the support? Can I take the floor joists spacing as segment with lateral restraint? Can anyone give me some examples? I have read some manuals but the examples they have are simply supported beams only. Thank you.

 

[human909]

You don't get to count the lateral restraints for wind uplift unless rotationally restrained e.g. fly braces. AS4100 counts wind uplift with lateral restraints on the tension/non-critical flange as completely unrestrained.

Agreed

The main take away for me here has been that constrained axis LTB kicks ass. And that effect should be significantly in play regardless of which flange gets the constraining.

That is not comfirmed by code nor buckling analysis.

 

[HS_PA_PE]

KootK - I'm in the US and have had little exposure to AS 4100, so I can't speak to the theoretical background or how it is regularly applied. I'm trying to gain understanding and hope that my ignorance is not taken as offensive to anyone. Here is a worked example from "Steel Structures Design Manual To AS 4100" First Edition by Brian Kirke, Senior Lecturer in Civil Engineering Griffith University and Iyad Hassan Al-Jamel, Managing Director ADG Engineers Jordan.

Maybe there is effectively zero possibility within the practical limits of real world construction of an LTB mode (constrained axis LTB) occurring before yielding with the compression flange fully restrained.

 

[KootK]

The main take away for me here has been that constrained axis LTB kicks ass. And that effect should be significantly in play regardless of which flange gets the constraining.

That is not confirmed by code...

1) You'll have to forgive me if I don't feel constrained on this by the lack of explicit code approval from a code section that no one can tell me the theoretical basis for.

2) Things like this are precisely why I seek to understand the theory behind code clauses. It gives me the ability to, and the ethical justification for, extending code provisions. That, rather than being a slave to their literal interpretation like an unthinking robot.

That is not confirmed by...buckling analysis.

3) Fantastic. I love being proven wrong in the present so that I can be more often right in the future. Please post the details of that buckling analysis.

 

[KootK]

KootK - I'm in the US and have had little exposure to AS 4100, so I can't speak to the theoretical background or how it is regularly applied.

No problem at all. For something like this, it's just important to know the background of the person behind the ideas. In your statements, I was hearing a lot of echoes of my own thinking which led me to suspect that we may have similar backgrounds when it comes to steel design. While I values your opinion very much, I'm sure that it will come as no surprise to hear that, on this topic, I'd value it even more if you were an Aussie practitioner. That whole "horse's mouth" thing, you know?

Here is a worked example from "Steel Structures Design Manual To AS 4100" First Edition by Brian Kirke, Senior Lecturer in Civil Engineering Griffith University and Iyad Hassan Al-Jamel, Managing Director ADG Engineers Jordan.

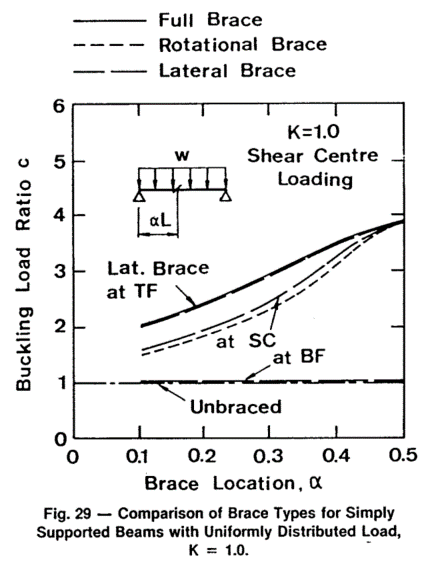
Thanks for the example. It's definitely more cut and dry with simple span beams and continuous compression flange bracing. I'm fairly certain that all codes give you a pass on LTB in that situation. That said, I agree with your base point that I would reiterate in my own words as follows:

1) The number of possible modes of instability is theoretically infinite.

2) The number of modes of instability of real practical concern is quite limited.

3) It is the purview of both design standards and design engineers to intelligently navigate the juxtaposition of #1 & #2.

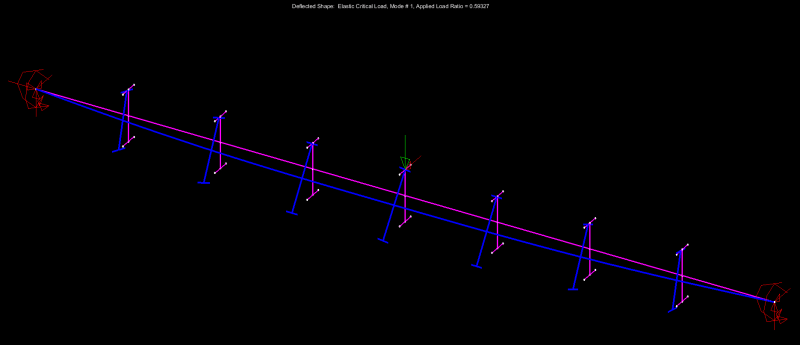
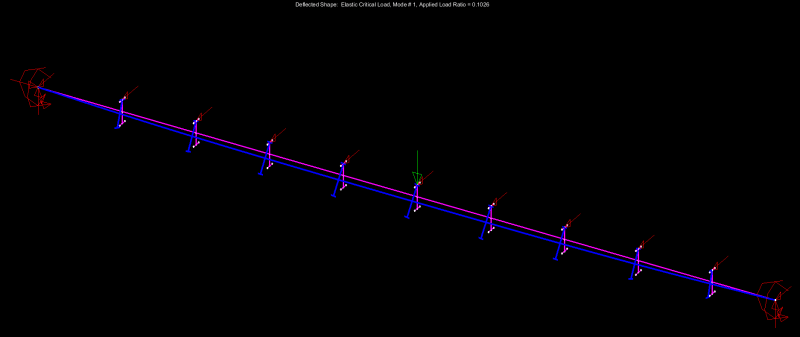
Maybe there is effectively zero possibility within the practical limits of real world construction of an LTB mode (constrained axis LTB) occurring before yielding with the compression flange fully restrained.

That is most definitely the case and is why I've been describing the LTB checking of the examples as effectively:

4) Check LTB of the constrained axis buckling mode as I've described it OR;

5) Trust that #4 is bloody awesome and check nothing at all.

The key feature there is simply to recognize that, if you are going to bother checking any LTB mode, then recognize that the only meaningful check is the constrained axis LTB mode. That, at least as far as it pertains to North American practice where we tackle instability phenomena in a hierarchical fashion as we've already discussed.

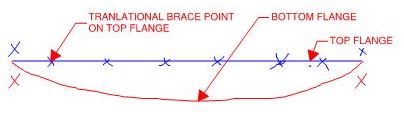
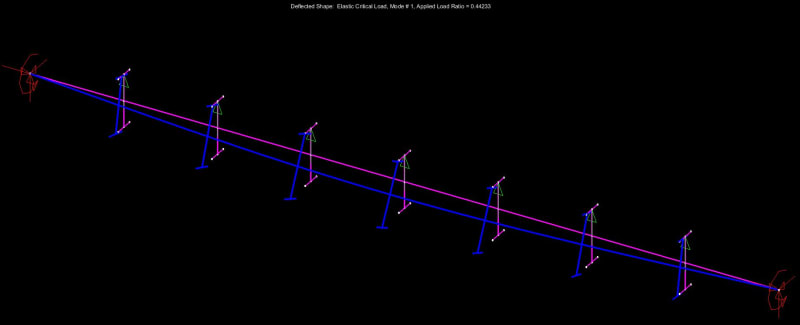
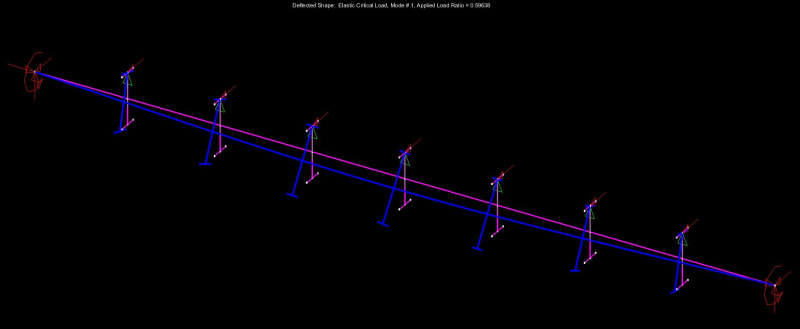
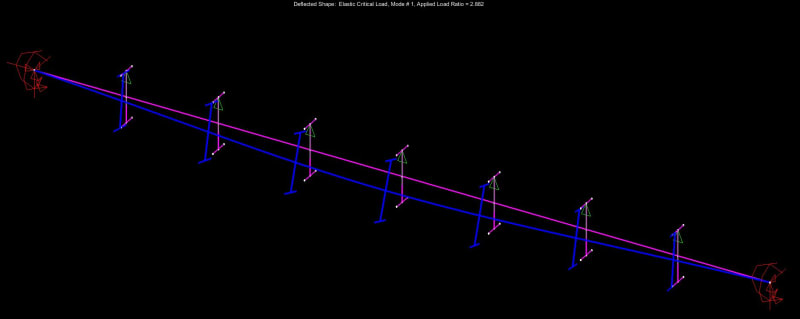
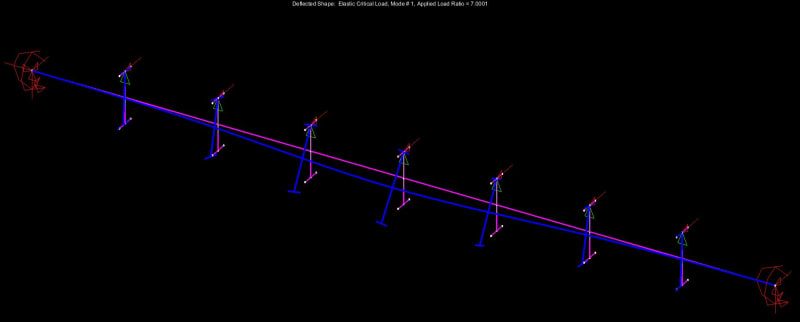
The infinite nature of instability is something that seems to factor heavily into the confusion that often surrounds free cantilever design. In that case, you're dealing with a couple of separate LTB buckling modes that occur in unusual close proximity to one another from a potential/strain energy perspective. The top flange is your most effective first brace point but, then, push things a little further and you'll have the bottom flange flopping out to the side. These are really two separate LTB modes rather than a single one. I suspect this is why some codes conclude that you should just be bracing both flanges if your really want to tax a cantilever.

Because no one else will do it for me, I've been trying to generate some high level theoretical explanations of AS4100 of my own. It's still a work in progress but one candidate for "how does it work" is something like this:

1) Only actually give explicit consideration to one buckling mode: the completely unrestrained mode. If capacity is insufficient, add your first brace.

2) Effectively "over-brace" the unrestrained LTB mode by adding more restraints to that LTB mode even though that LTB mode ceased to be a physical possibility, or the critical LTB mode, once the first brace was added.

3) Make the argument that the over-bracing of the unrestrained LTB mode from step #2 effectively eliminates the possibility of any subsequent LTB modes from coming to pass.

I think that this would be consistent with what you're suggesting (and I agree with). There are some big logical gaps to fill in that explanation but, at the least, it would resolve these issues that I have with understanding the AS4100 procedure:

A) How does it address all LTB modes by explicitly considering only one LTB mode (or no actual buckling mode, I'm not sure)? You know, if Human909 is right about that being the case.

B) How can it be that the effective length used is something other than the actual buckling length of the thing doing the bucking? That this is true is clear now from the Yura paper, the FEM models, the design example, and reasonable expectations of physical behavior.

 

[Settingsun]

I'm a bit busy to think about the deeper and more meaningful questions posed in the past few days but here's some quick input.

Sorry. What? How do you figure this?

The hand check numbers are from your Space Gass output and the capacity according to the elastic buckling method is taken from Agent666's Cases 2 & 3. Cases 2 & 3 are the same according the the AS4100 hand method (they differ only by a lateral restraint to the tension flange) and Agent got similar results for the two. Case 3 just made it to the section capacity while case 2 fell about 3% short. Hitting section capacity is what keeps the final result similar between hand calc and elastic buckling but I think there would be other cases where the difference is larger and I think that would be unconservatism on the part of the hand calculations.

My impression here is that many of us, myself included, lack a cogent theoretical understanding of just how the AS4100 provisions work their magic

What are the major differences to AISC? It looks to me that, aside from L restraints on segments with moment reversal, they're pretty similar. Our L_e calculation may have a bit more to it. Is there more?

I'm at the point of wondering whether L restraints with moment reversal are something not handled well by AS4100. Perhaps the rule was derived from considering simply-supported beams but applied generally. See graph at the end.

I could run it in Mastan. I may do this eventually but I wouldn't hold your breath.

I don't know how to run it in Mastan (on the to-learn list). That's why we prevail upon the generosity of Agent666 (please). I'd like to run the W27x84 in the following cases:
- The 32-foot span with just one L restraint to top flange at midspan; and
- The 22 metre span with top flange L restraints at 1.1m.

Would you say that the lateral brace at [2] makes this truss immune to LTB?

I don't like the look of node 4. That aside, K_l=1.0 doesn't mean immune from LTB, it means no more exposed to LTB than for shear centre loading. But I now agree that top flange loading at a top flange L restraint should use K_l>1.0 if the bottom flange is going to move sideways.

When do people use P restraints? I can’t recall ever bothering with them.

They might be free or geometrically preferable to F restraint whilst almost doing the same job. I've attached some guidance on what is F/P from an article in the Australian Steel Institute Journal from 1993 (by Trahair, Hogan & Syam).

https://files.engineering.com/getfi...-7e97854bb7d9&file=LTB_restraint_guidance.pdf

AISC procedure on a theoretical basis and feel confident in saying that it is built around Lb being the distance between points that would be, in Aussie parlance, the distance between F/P restraints

AISC 360-16 Section F2.2 says "Lb = length between points that are either braced against lateral displacement of the compression flange or braced against twist of the cross section." That's AS/NZS F, P or L restraint, isn't it? At least for beams without moment reversal. And the difference for moment reversal is the unwritten law that "the" compression flange is both flanges.

ere I a martian spending my first day on earth, my interpretation is how I would read 5.5.1.1 from the get go. I was surprised to learn that it is not, in fact, interpreted as I have outlined.

AS1250, the allowable stress predecessor to AS4100, said: "The critical flange of a member is that part which would deflect the furthest during buckling in the absence of the restraint being designed." I agree with that. I think it's also what you're saying.

It is definitely easier. But is it more correct? If the compression flange definition and the max movement definition ever find themselves in conflict, it is my opinion that it is the compression flange definition that should take a back seat.

My opinion is that moving furthest is more correct hence mentioned first, while compression flange is the simplification for ease of routine design. Compression flange is self-reliant and easy to determine whereas moving flange depends on the other restraints and is less easy to determine. Quoting again from AS1250, the compression rule of thumb is filed under 'if an exact analysis is not available'.

The main take away for me here has been that constrained axis LTB kicks ass. And that effect should be significantly in play regardless of which flange gets the constraining

Bottom flange L restraint in a simply supported beam under gravity loading does nothing for capacity. I can't find much else regarding tests or analysis of L restraints, which is why I wonder whether simply-supported results were just extrapolated to applying universally. The graph below shows results of elastic buckling analysis. Note also Agent666's case #1 rotated about the bottom flange anyway so bottom flange restraints wouldn't be stressed.

A) How does it address all LTB modes by explicitly considering only one LTB mode (or no actual buckling mode, I'm not sure)? You know, if Human909 is right about that being the case.

B) How can it be that the effective length used is something other than the actual buckling length of the thing doing the bucking? That this is true is clear now from the Yura paper, the FEM models, the design example, and reasonable expectations of physical behavior.

A) I'm not sure it is just one mode. We have to check all segments but often it's obvious which will govern. I think in the W27x84 case they represent different modes as different flanges are critical.

B) The effective length combined with the alpha_m factor is meant to relate to the capacity of a beam under uniform moment. I can imagine that the length would get a bit abstract when the moment is nothing like uniform.

 

[KootK]

I don't know how to run it in Mastan (on the to-learn list). That's why we prevail upon the generosity of Agent666 (please). I'd like to run the W27x84 in the following cases:
- The 32-foot span with just one L restraint to top flange at midspan; and
- The 22 metre span with top flange L restraints at 1.1m.

I agree, Agent666 & Human909 have been carrying more than their share of the load on the modelling front. To help rectify that, and to to have some fun of my own, I'm going to take a swing at both of your proposed models. I'm also going to include links to my Mastan files for the benefit of anyone who would like to critique them or use them or as convenient starting points for their own exploratory modeling. The slowest part of getting started is figuring out how to do build a functional model that delivers what you need. And drawing those stupid faux cross sections so that you can see the twist.

For your 32 ft example, see the plot below and this Mastan file: Link. Quick notes:

- Elastic critical analysis.
- No imperfections modeled so a high side estimate.
- Fy inflated to ensure an elastic buckling failure mode.
- No weak axis rotational restraint at the ends.
- Applied Load Ration = 0.59
- Fails at 0.59 x 250k = 147k
- Clearly a version of the constrained axis buckling mode that I've been droning on about.

 

[KootK]

I'd like to run the W27x84 in the following cases...the 22 metre span with top flange L restraints at 1.1m.

To clarify and update others on the situation that I believe we are testing, my understanding is that we're querying this:

I think there might be a quick and easy first test we can apply. Taking the W27x84 and the same bi-linear shape of the moment diagram from the test case, I reduced the maximum bending moment to 1240 kNm which is the design section capacity phi.Ms. I then increased the sub-segment length until the AS4100 LTB capacity phi.Mb = phi.Ms. The sub-segment length was 5.065m (ie from end of beam to the inflection point) giving overall beam length of 20.26m before LTB governs according to AS4100.

Your example was clever. Me likey. As I understand it, the crux of the example was to exaggerate the length of the original problem until constrained LTB did in fact occur; and, in doing so, suggesting that it would take a rather ridiculous span to make that happen (66.5 ft).

So the exact numbers here have been drifting a bit. And, because of the way that Mastan is sort of unit-less and has canned AISC sections in inches, it's much easier for me to work with spans and segment lengths that are in even increments of inches. So I tweaked your numbers a bit but, I suspect, the analysis will still serve the purpose that you'd intended.

For this example, see the plot below and this Mastan file: Link. Quick notes:

- Span = 70 ft = 21.3m
- Sub-segment length = 7 ft = 2.13m (10th points. Probably doesn't matter much as long as it's close enough to force the constrained axis buckling mode.
- Elastic critical analysis.
- No imperfections modeled so a high side estimate.
- Fy inflated to ensure an elastic buckling failure mode.
- No weak axis rotational restraint at the ends.
- Applied Load Ratio = 0.1026
- Fails at 0.1026 x 250k = 26k point load
- Fails at 2768 kip*in end moment = 313 kN*m (25% of your phi.Ms. value of 1240 kNm)

CONCLUSION: if I've not screwed anything up, I believe that this would suggest that the beam length at which constrained axis LTB would occur can be expected to be significantly shorter than the value at which AS4100 would predict that LTB would govern over phi.Ms.

SURPRISE OBSERVATION: the moments at the ends are different from the moments in the middle. I should have anticipated this, in retrospect, but did not.

 

[Agent666]

You don't need to model any imperfections with the elastic or inelastic critical load analyses. It is effectively an eigenvalue analysis solving the governing equations for the modes and hence reference buckling moment and alpha_m directly. The imperfections are dealt with afterwards in the AS4100 and NZS3404 methods as per the example I wrote up on the screenshot by applying the alpha_s factor. If you're doing any of the 1st/2nd order equations then you explicitly need to model the imperfections and set up the residual stress model, and of course include warping.

The only thing you need to ensure if doing the eigenvalue analysis is to enable warping (why it's not turned on by default....), but only on the main beam, not on all the bits to visualise the twist, because it changes the answer when it should have no effect.

I was also getting elastic buckling without jacking up f_y.

It's important to recognise that the moment at which buckling occurs in the analysis is not the design capacity. So don't compare these moments directly. edit... Bolded for super importance!

I mentioned as well that because you're dealing with a centerline model with restraints off the centerline, the stiffness of bits to visualise the web twist comes into play. How stiff to make it, really don't know but I found taking a member the same thickness as the web and making it as wide as the beam depth kind of cake up as a lower bound.

I didn't review your file, just generalising comment for anyone using mastan2.

I actually think in hindsight the case #2 I did I screwed up the calc because I think I still looked at the total length when I should have been looking at 8' or 12'. That's what I get for trying to do it on the calculator on my phone. So it will have FLR, no 3% shortfall.

 

[Agent666]

Mastan2 has metric sections also. The unitless thing can get confusing. So best to stick to what you know and convert end answer.

If you've not got the same moment then I think you've applied the wrong moment to balance the load you put at the center?

 

[KootK]

I didn't actually apply any end moments. I just fixed the ends to produce the same result as I figured that would be simple and dummy proof. I suspect that its something to do with equilibrium being enforced on the buckled shape. The end moments would presumably rotate in space about the z-axis, just like the ends themselves.

 

[Celt83]

KootK:
Does mastan2 consider shear deformation, that could be one factor for the different fixed end moments.

Agent666:
If I understand the value taken from the buckling analysis replaces the Fcritical value used in the LTB check, is that accurate?

 

[KootK]

KootK: Does mastan2 consider shear deformation, that could be one factor for the different fixed end moments.

I'm not really sure. It takes in [mu] and [E] so it could calculate [G]. And my guess is that the Ayy and Azz are shear areas that I currently have set to infinite. I speculate that Mastan can include shear deformation but, as I've been using it, has not been. Unfortunately, it's not the kind of program where you can just click in a box and push F1.

You should just get Mastan. It's free and you'd love it.

Agent666: If I understand the value taken from the buckling analysis replaces the Fcritical value used in the LTB check, is that accurate?

On a related note, I'd like to explore some things here that do take account of imperfections etc. And, if possible, I'd like us to agree to a common way of handling that, be it the AS4100 method or something else. So I'm in the market for recommendations if anyone has any. I'd like it to be simple, if possible, to limit the time investment. One option I'm considering is this:

1) Look up the AISC tolerance on beam sweep.

2) Apply a torsion to the beam at the load point equal to the vertical load multiplied by the sweep. So T = P * L/1000 or something like that. Essentially just a perturbation.

 

[KootK]

Secondly, once I get myself right with AS4100, I intend to never, ever again bother checking LTB on joist loaded floor girders unless they're cantilevered. This is clearly where AS4100 takes us to in the end. And it will be a nice little, lucrative take-away for me from this exercise. I postulate that the same may well be true of roof girders although owing to the same constrained axis effect even if the bottom flange is everywhere in compression.

With Mastan set up on my virtual machine, it seemed easy enough to just test this and put it to bed.

All cases: W27x84; 32ft; 35 kip uplift loads at 1/8th points; total load = 245 kip; elastic critical run; no week axis rotational restraint at ends.

Case 1: simple span beam with no L-restraints. ALR = 0.44233; Total Load = 109 kip

Case 2: simple span beam with L-restraints. ALR = 0.59638; Total Load = 146 kip

Case 3: fixed end beam with no L-restraints. ALR = 2.882; Total Load = 706 kip

Case 4: fixed end beam with L-restraints. ALR = 7.001; Total Load = 1715 kip

CONCLUSIONS:

A) For the simple span case where the bottom flange is everywhere in compression, the improvement was not as much as I'd hoped at only about 34%. Looking at the deflected shapes, it seems that this is because the unrestrained center of LTB rotation is pretty much at the roof deck level anyhow so not much changes by adding the deck.

b) Once end moments are introduced, the improvements come fast and a constrained axis LTB failure seems improbable. This jives with the AS4100 method which would have counted several of the top flange restraints as L-bracing at the ends of the beam. And I think that I might see why now. Once your get both flanges trying to do some buckling, the LTB mode becomes skewed more towards the lateral than the torsional. This pushes the center of LTB rotation up further above the top flange and makes the the L-restraints that much more effective.

 

[Agent666]

If I understand the value taken from the buckling analysis replaces the Fcritical value used in the LTB check, is that accurate?

Not quite, in AISC I believe you replace F_e the elastic buckling stress, then evaluate F_critical normally from there! It's basically the same in AU/NZ standards, instead of working in stress which is fairly meaningless, we work in moment. Elastic buckling moment is equivalent to elastic buckling stress, Fcrit is equivalent to member moment capacity M_bx.

So in AISC there is a codified way of taking account of any restraint condition imaginable, backing up the assertion that any restraint to the compression flange can in fact be used as essentially AU/NZ standards have the exact same provisions, a buckling analysis quantifies the effect. I linked to an article earlier that suggested AISC doesn't account for initial imperfections so there are some differences in the underlying stuff though.

So in conclusion you can do a buckling analysis to work out the elastic buckling stress, clause E3 states this explicitly (see below). Once you have this from a buckling analysis then you carry on as per normal design.

So keeping this in mind, if you're ignoring any intermediate restraints that a buckling analysis might show are effective you're potentially being very conservative (obviously every scenario is different), even if that's the way the examples and hand checks show to AISC.

I hope my earlier case #1 demonstrated that the buckling analysis route gave exactly the same result as codes theoretical approach. Now as things get more complex, a buckling analysis is still going to give the theoretical buckling moment (and allow for calculation of the exact alpha_m instead of using a curve fit equation), the code provisions might for the sake of needing to cover 1001 cases give a (hopefully) conservative all encompassing answer.

What the buckling analysis does allow you to get into is say you have a rotational spring as a restraint, you can evaluate this directly as its neither pinned with no rotational restraint, nor is it fixed with no rotation. This is the beauty of using a buckling analysis, you're simply working out the theoretical buckling moment but directly for any restraint condition imaginable. The moment value coming out of the buckling analysis is exactly in the form expected by the code to then go on and apply your normal buckling curves modifications to account for the 2nd order effects (initial imperfections, out of plumbness, residual stresses, etc, in AU/NZ speak this is the alpha_s factor).

You can apply the imperfections directly in mastan2 using the update geometry tool (you'll find some videos by the author on youtube showing you how to do this).

But as I noted, it's not of importance if you are doing the code implied eigenvalue analysis, by this I mean get buckling moment, apply normal code reduction, get equivalent capacity.

If you go through the mastan2 stability fun modules, it takes you through each type of analysis and compares answers. The upshot is if you allow for all the second order effects and use the 2nd order elastic or inelastic analysis you'll get pretty close the code curve which indirectly allows for these things (these analyses are more your full on FEM type of thing that gives you the capacity directly because you've allowed for the 2nd order stuff and don't need to apply the code curve reductions (i.e. alpha_s in AS4100/NZS3404 terms).

Screenshot below of my attempt at this when I went through it a year or two ago with both AISC and NZS3404 results. Shows the importance of allowing for warping and imperfections. Note where the default AISC curve sits relative to the L/1000+ warpingresidual stress curve relative to the NZS3404 kr=1.0 curve. The Adina FEM results were provided by the author for comparison, you work out all the rest as part of the stability fun exercise if you want to go down that rabbithole! (I highly recommend it if you have hours to spare, and I mean hours (per module)....).

direct link to full size picture

 

[Tomfh]

I've attached some guidance on what is F/P from an article in the Australian Steel Institute Journal from 1993 (by Trahair, Hogan & Syam).

Thanks for that. Most of those P connections I never use, but good to know.

Interesting that they count a fly brace on unlapped purlins as P. “Design of Portal Frames” says to not bother and take kt=1.0 at fly bracing.

Perhaps the rule was derived from considering simply-supported beams but applied generally.

It needn’t just be simply supported cases. As noted by others above, for gravity loads the top flange is often the best place to buckle, period, even in continuous beams when the top flange has gone into tension. That is to say the top flange will often buckle the furthest, even in tension zone. Bracing it boosts buckling capacity more than the bottom compression flange, contrary to the “compression flange is critical” rule. (Vice versa for wind uplift). From memory the old code AS1250 reflected this. It specified critical flange for gravity as top flange, and bottom flange for wind.

Then they changed the simplified rule to “compression flange is critical”, which emphasises moment reversal - even through moment reversal isn’t actually that relevant to LTB - (buckling shapes do not mirror bending moment diagrams)

The current rule covers cases where bottom flange compression is really important (say a deep haunch), and still probably good enough even when the tension flange is the real critical flange - which is a lot of the time.

 

[Tomfh]

A) For the simple span case where the bottom flange is everywhere in compression, the improvement was not as much as I'd hoped at only about 34%. Looking at the deflected shapes, it seems that this is because the unrestrained center of LTB rotation is pretty much at the roof deck level anyhow so not much changes by adding the deck.

Yes, you’re grabbing it in a place it doesn’t move much, so grabbing it there doesnt do much.

This is what we were saying before, hence AS4100 saying no restraint for you if you grab it there.

 

[KootK]

Yes, you’re grabbing it in a place it doesn’t move much, so grabbing it there doesnt do much. This is what we were saying before, hence AS4100 saying no restraint for you if you grab it there.

I'm afraid that was not what you said before Tomfh. What you said before was basically "AS4100 says no". What would have been more useful would have been "AS4100 says no and the thoeretical reasons for that are X, Y, and Z". You know, the "why" versus the "what". Instead, I had to chase down the why myself this morning.

Besides, it's not like a 34% improvement is nothing. Clearly, grabbing the tension flanges for the constrained axis LTB effect is doing a fair bit, even for simple span beams.

 

[Tomfh]

We weren’t saying AS4100 says it for no reason.

It’s obvious why laterally bracing a non critical flange (ie laterally bracing close to the centre of rotation) is generally considered ineffective. Because the beam can still fall over. You’re adding your pin at the pivot point, where it does far less. That’s exactly what happens in these situations. The beam can just flop over, pivoting about the restraint.

When you brace the part that wants to move (aka the critical flange) you inhibit that rotation from occurring at that section.

 

[KootK]

We weren’t saying AS4100 says it for no reason.

I didn't say that you said it for no reason. I said that you didn't provide the reason. I don't read minds.

It’s obvious why laterally bracing a non critical flange is generally considered ineffective

It wasn't obvious to me. Nor should it have been as a 34% improvement is still a fair amount of improvement, particularly for the most extreme of cases (100% bottom flange in compression)

And yes, I get the mechanism. I described it myself earlier.

looking at the deflected shapes, it seems that this is because the unrestrained center of LTB rotation is pretty much at the roof deck level anyhow so not much changes by adding the deck.

These two statements of yours now seem to conflict. I'm basically just agreeing with the first one.

It is a bit sad though that the simplified rules have led so many engineers into believing that the compression flange is always the best place to brace, and that bracing the tension flange is automatically inneffective.

It’s obvious why laterally bracing a non critical flange is generally considered ineffective

 

[Tomfh]

And yes, I get the mechanism

Ok good. Then you understand why AS4100 considers it ineffective. Not sure why you needed to fight over it.

These two statements of yours now seem to conflict.

They’re not in conflict.

The first statement refers to the AS4100 rule that “the compression flange is the critical flange”. This rule (and the background to it) is murky, and does lead to some confusion about the actual best place to brace. It incorrectly identifies some compression flanges as “critical” when they aren’t actually the critical flange. But as noted it is good enough to treat the compression flange as the critical flange, even when it isn’t really the critical flange.

The second statement refers to the rule that says it is ineffective to laterally brace a non critical flange. The “theory” behind the rule is obvious. We don’t seem to disagree on it.