L-Brace said:
Can you define and L-brace and a P-brace?
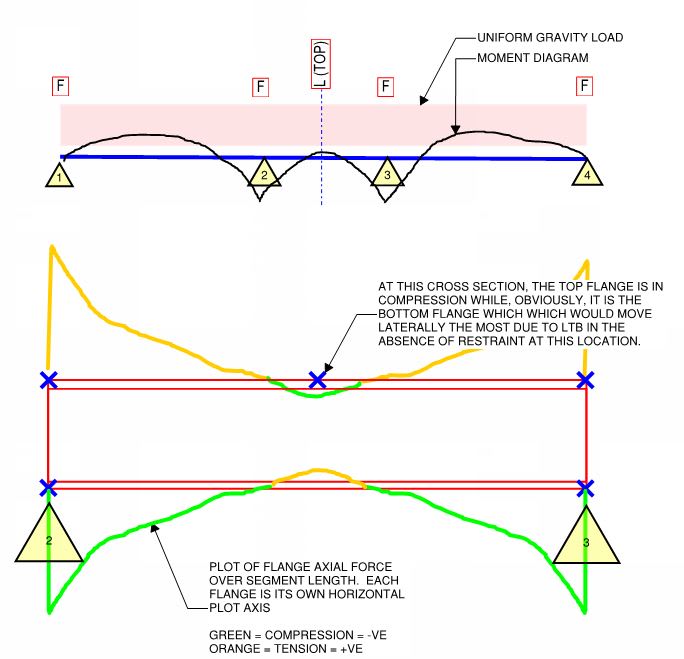
L-brace: Aussie for just straight up lateral (L) support without providing any torsional restraint to the beam. Usually this is how own would conservatively treat a steel joist tying in.
P-brace: Aussie for a full fixity brace (lateral + torsion) that only does a partial (P) job of being a full fixity brace. An example would be a top side purlin moment connected to the beam supported to it
without a stiffener pair on the beam. In reality, all open webbed steel joist connections are somewhat a version of this.
RFreund said:
It seems like everyone has agreed that it should be defined as the length between "columns"
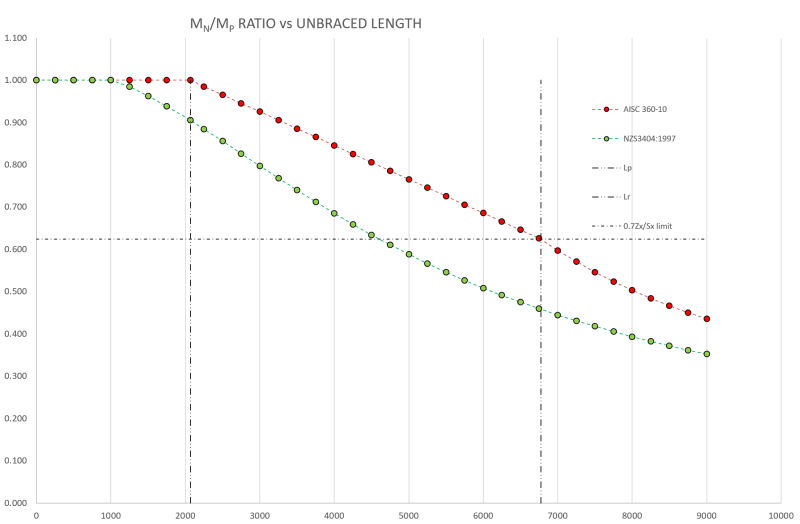
Oh no, not at all. Me, Yura (read that attached paper), and most AISC practitioners see it that way. The Aussie code seems not to and treats the effective buckling length as the length between L-braces. This was the initial source of contention. At this point, we've established that the AISC and AS4100 methods are practiced quite differently. My current bones of contention are these:
1) I don't understand the underlying theory that justifies AS4100 treating the unbraced LTB length as something much shorter than it obviously is in the real world (distance between points of twist restraint) and;
2) The AS4100 method seems to operate on a single, unrestrained LTB buckling mode rather tackling the multiple, possible modes in a hierarchical fashion as we do with AISC. Again, this is a theoretcial understanding issue for me. I just don't undertand how AS4100 works the magic that it seems to. I want a look at the wizard behind the curtain.
RFreund said:
Then it seems we discovered there is some benefit to having the top of the beam braced against lateral translation even when checking the end (negative) moments. This benefit is or is not codified?
I wouldn't say that it was
discovered here. I've been mentioning the constrained axis buckling check since the very beginning and extolling its virtues in improving capacity. This is the effect that you've described. As for codification:
1) The base method in the AISC SCM does not account for this.
2) The are AISC documents, such as the Seismic Design Manual, that do provide guidance for constrained axis LTB checking.
3) Frankly, it's hard to say if AS4100 explicitly checks constrained axis buckling or not as nobody seems to really be able to explain how AS4100 actually works. Certainly, the
outcomes are much closer to #2 above than they are to #1. And that makes me suspect that, one way or another, AS4100 is dealing with constrained axis buckling.