KootK said:
Verifying that this is how AS4100 works
A situation where appeal to authority is the only option. You must be in uncomfortable territory! I've attached a paper by Trahair et al explaining AS4100's lateral buckling method. For those who don't know, Trahair was the co-chairman of the committee that developed AS4100 and was probably 'the guy' on the lateral buckling provisions. Yura might be the US equivalent (?)
Some sections that are relevant to the various directions this discussion is taking are:
- 4.1.4: "Despite this lack of restraint against twist rotation, laterally-restrained intermediate cross-sections... act effectively as if fully restrained." But for just the equivalence of L restraints to F restraints in AS4100 I don't think we need this article. You would only need to look at one page of the code I think - the tables for the factors that contribute to effective length L_e. Anywhere there's an option for L restraint, substitute F restraint and the factor is the same. FF = FL = LL and FP = PL. (Except k_r as noted before.)
- 4.1.5: "Cross-sections that are not effectively prevented from deflecting laterally are treated as unrestrained in AS4100, no matter how effective the restraint against twisting may be", then suggesting that design by lateral buckling can be used if this is considered too conservative.
- 4.3.3: Load height factor at point of lateral restraint. See the 5th paragraph. This seems to imply that a bottom non-critical flange won't move sideways at all when the top flange is L-restrained. Perhaps the case without moment reversal, see below.
KootK said:
Justifying that this approach is theoretically appropriate.
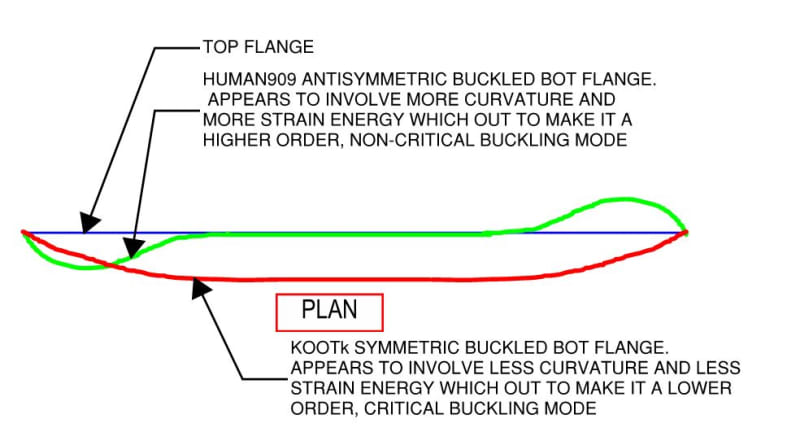
I haven't done an exhaustive literature review and am not capable of doing so, but when I do read about LTB it seems that simply-supported beams without moment reversal are very commonly the case that is considered unless moment distribution is specifically being investigated. Then the simply-supported case is assumed to apply generally without any rigorous proof. Since first coming to this topic, I have wondered if that is the case with L restraints. That graph I posted that shows critical flange L restraint exactly equalling F restraint (like in AS4100) and non-critical flange L restraint doing exactly nothing (like in AS4100) was for the simply supported case - no moment reversal. The paper it comes from only covers simply-supported and cantilever beams: top flange always critical. The paper is Australian, from 1986 (a few years before AS4100 was first published in 1990) and you can see how the AS4100 rules would be a conservative simplification for the cases covered. My suspicion is firming that the AS4100 L-restraint rules were written without any consideration of moment reversal.
Tomfh said:
I’m not sure how an L can really be as good as F in reality, or how L on non critical flange can do literally nothing...
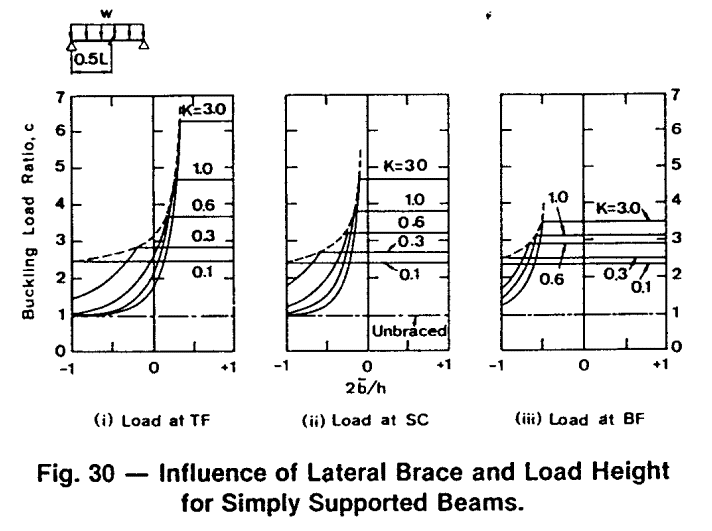
It's complicated. Here's a fuller picture. Note for beams where St Venant torsion dominates over warping torsion (K=0.1), the restraint location on the cross section doesn't matter at all. 2*b_bar/h = -1 is the bottom flange (b_bar is the brace distance above the shear centre/centroid).

![[rednose] [rednose] [rednose]](/data/assets/smilies/rednose.gif)