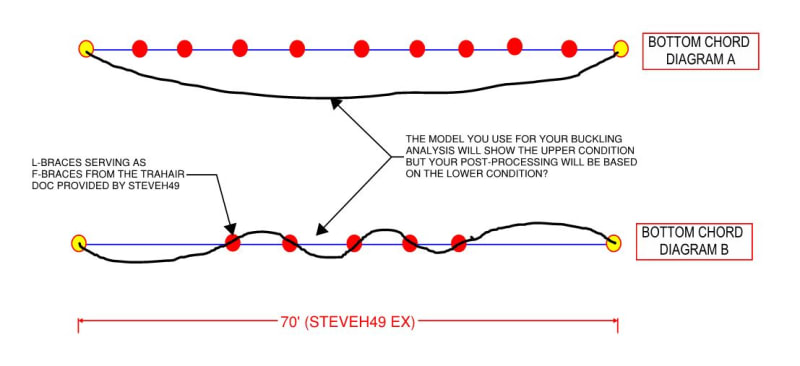
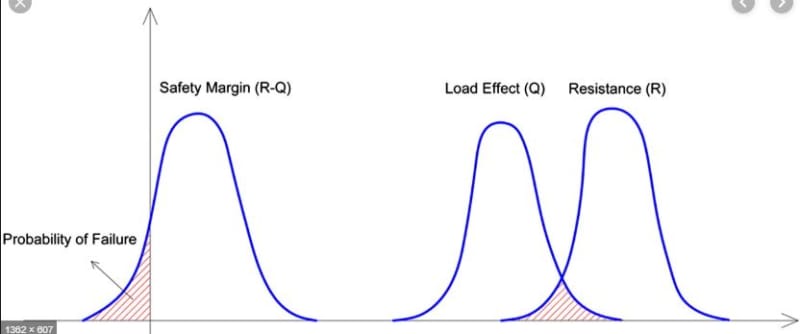
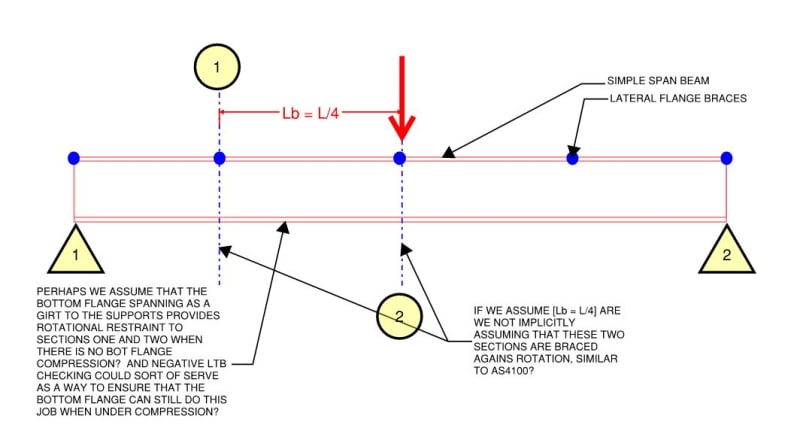
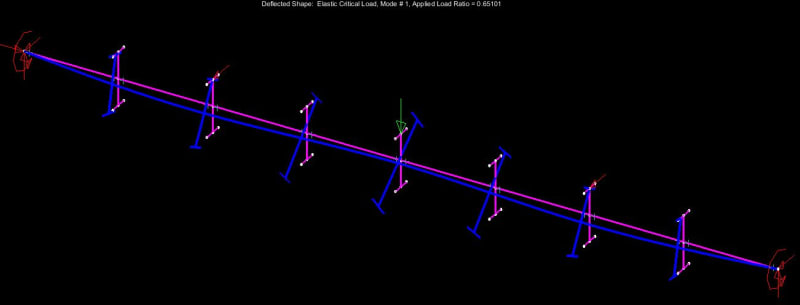
Agent666 said:
Can you confirm you are doing this please when comparing these numbers?
Not confirmed. I am most definitely not doing that.
KootK said:
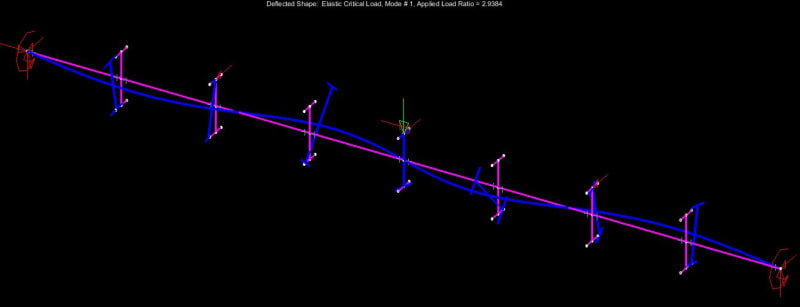
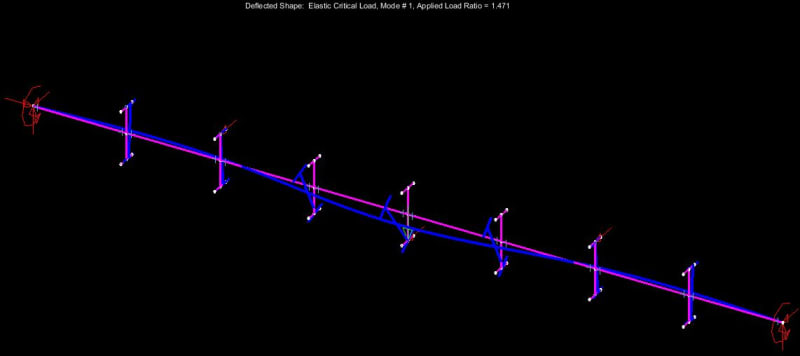
Mastan elastic critical buckling, sans imperfections
Agent666 said:
I'll say it again, you don't need imperfections modeled when doing the eigenvalue analysis (elastic critical load analysis in mastan2).
I realize that imperfections don't need to be modeled to run an eigenvalue analysis. However, the results of an eigenvalue will not reflect the decrease in capacity resulting from imperfections if those imperfections are not given explicit consideration in the buckling analysis model. It was this latter point that I meant to convey. I'm trying to ensure that anyone reading the results does't erroneously assume that some consideration has been given to imperfection in my Mastan runs when it has not.
Agent666 said:
Kootk, aren't you actually comparing the As4100 capacity to AISC capacity to a elastic critical buckling moment though?
Absolutely, and that is by design.
Agent666 said:
They are two different things and not comparable in any way. I've said it a few times now in the thread but if I'm reading it right people don't understand me or something? The mastan2 buckling moment is not the design capacity.
I thought that'd I'd already explained this...
Agent666 said:
You all need to stop quoting the reference buckling moment directly as a capacity, it isn't!
KootK said:
"You all" is a pretty big bucket. Does it include my work? It shouldn't. Two perfectly valid things can be done with the reference buckling moments from FEM:
1) Compare one reference buckling moment to another so suss out the impacts of various changes to the situation.
2) Use a reference buckling moment as an upper bound capacity.
I believe that I carefully placed all of my stuff into one of those two buckets with statements like the one below that I included along with my modelling results.
I believe that valid comparisons can be made and I am confused by your assertions to the contrary. I think that one just has to understand the nature of what is being compared. So I'll just tell you what I had in mind in greater detail and you can let me know what parts you object to:
1) For both AISC and AS4100, I take the adjusted LTB values coming out of Mastan as
upper bounds to the true capacity. As far as I know, any subsequent adjustment factor such as phi_b or alpha_s only serve to lower the capacities generated by Mastan.
2) I take both the AISC and AS4100 design capacities calculated the traditional way as
lower bound capacities.
3) If I find that the upper bound capacities coming out of Mastan (#1) are lower than the lower bound capacities coming out of AISC/AS4100, then I conclude that there's a problem that needs sorting (tomfh's last point I think).
4) I don't worry about converting the raw Mastan values to code appropriate, buckling analysis design values because any such conversion is only going lower the Mastan capacities and exacerbate any problems discovered in step #3). What was a problem at #3 just becomes
more of a problem.
Are these not valid comparisons to make?
For an AISC audience, things work out great as AISC doesn't consider imperfections for LTB and the Mastan values are effectively [Mn] as far as I know. This is perfect for comparison.
For an AS4100 audience, I believe that I'm effectively providing [Mb/alpha_s]. Clearly, further post-processing isn't required to identify the discrepancies that currently concern us but, if anyone would like to undertake such post-processing, they are welcome to.