Rafter without fly brace? 22

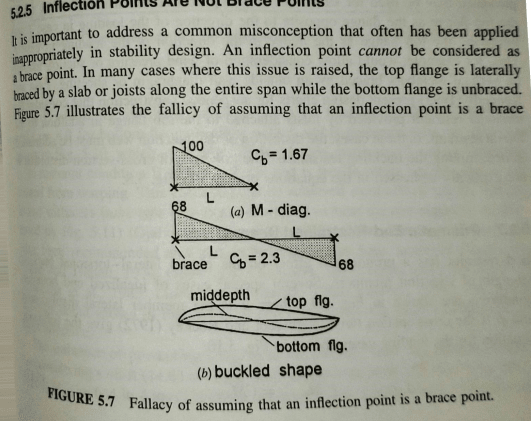
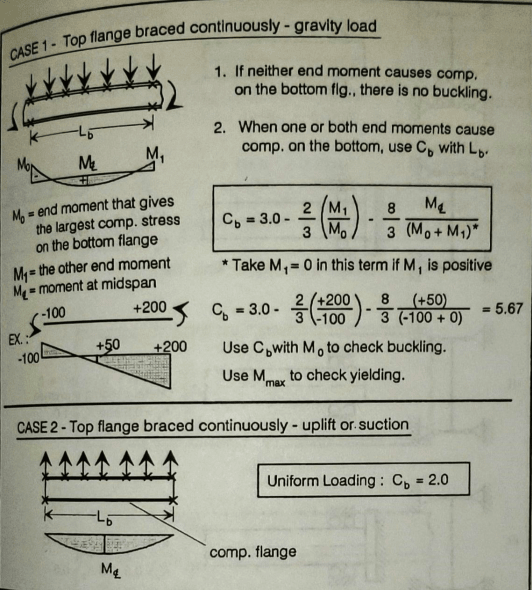
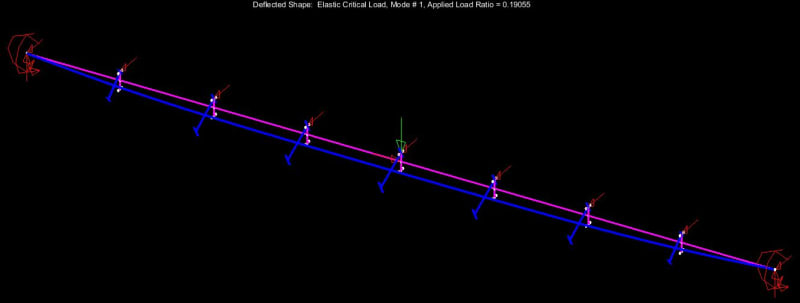
[fourpm]

I am designing rafters to AS4100 and wondering what if I don't use fly brace. I understand that with fly brace it will give you full restraint. But if I don't use fly brace, will the purlin above be considered as lateral restraint for rafter under uplift? If so. can I take the purlin spacing as segment and the only factor that changes without fly brace is kt?
I have the same question when it comes the continuous steel floor beam design where Z/C floor joints sit on top of the beam. What segment should I take for the beam near the support? Can I take the floor joists spacing as segment with lateral restraint? Can anyone give me some examples? I have read some manuals but the examples they have are simply supported beams only. Thank you.

 

[KootK]

How many times do I need to explain this... serious question?

It was indeed a serious question. Persuasion is really a game of quality rather than quantity.
Regurgitating a previously unconvincing argument repeatedly, and unchanged, doesn't gradually make it more persuasive. So, unless you can find a way to add a little more meat to your persuasion sandwich, you can bank on having to repeat your explanation indefinitely.

Tomfh, on the other hand, was killing it in persuasion department while I was fast asleep. Persuasion by way of a much simplified, yet highly analogous, example. Socrates himself would have been proud. I couldn't have done it any better myself so I won't bother to try. Are you truly not persuaded by the logic in the argument below?

Design capacity coming out higher than the unfactored buckling moment is not an irrelevant comparison.It’d be like if your pinned column capacity is coming out higher than its Euler buckling load.

Coming at this from the other direction because I'm not terribly familiar with aisc, what exactly are people reporting when quoting aisc capacities, is it a moment based on F_e?

My understanding is that the Mastan values would be straight up replacements for Fcr as it is defined below. That, because AISC gives no accounting of the impact of initial imperfections for LTB as AS4100 does via [alpha_s]. Note that [Cb] would then be based on a the entire member being the design segment rather than the sub-segments between L-braces as they are defined in AS4100. This is very much related to RFreund's comment below which I hope has not been glossed over as I suspect that it may hold one of the keys to sorting out our differences here. As I see it, the crux of things here is not what happens within a particular unbraced length but, rather, what the unbraced length should be to begin with.

I myself an a noob when it comes to doing LTB design via buckling analysis. So, if any AISC practitioners disagree with me on how such a design should be executed, I encourage them to come forward and show us how it's done for real. I'm happy to retract the claws for this part of the discussion.

@Agent666 I was reviewing some of the curves that you posted. It looks like they compare moment capacity to unbraced length which I suspect the AS4100 will be more conservative due to the equation. However, I assume they are both using the same unbraced length in this comparison. In the current situation we are using different unbraced lengths as directed by the code. So referring back to those curves doesn't seem to help in this situation.

 

[RFreund]

Hi RFreund, you're mixing a whole lot of ideas here that's going completely off target.

You're not multiplying alpha_s by Moa. You multiply the full plastic moment capacity (M_sx) by alpha_s x alpha_m x strength reduction factor. Moa is only required to calculate alpha_s. Otherwise it has no bearing on the capacity value or buckling values.

Damn, good catch. I will update my calcs. Updated, let me know.

I myself an a noob when it comes to doing LTB design via buckling analysis. So, if any AISC practitioners disagree with me on how such an analysis should be executed, I encourage them to come forward and show us how it's done for real. I'm happy to retract the claws for this part of the discussion.

Fairly certain you're on the right track here.

As I see it, the crux of things here is not what happens within a particular unbraced length but, rather, what the unbraced length should be to begin with.

Yes, I think things are coming full circle back to this. I will try to post more on this later.

Back to the GEN7001 Document:
This entire document is discussing portal frames and when it looks at a case for uplift with no fly braces it recommends using the entire length as unbraced acknowledging that a portion of the bottom flange will be in tension. So in this case they ignore the inflection point. Not sure how much weight I can put into this contradiction, just mentioning it.



EIT

http://www.HowToEngineer.com

 

[Tomfh]

The point is just getting people to compare apples with apples, not oranges with apples

It’s not an apples vs oranges comparison.

It’s a whole apple (predicted design capacity) vs half an apple (Mastan predicted buckling load).

The AS4100 elastic buckling design process reduces the size of the half apple even further. (The step you’re complaining isn’t being done).


We appear to be missing some of our apple. If you can point out where it is that’d be very helpful!

 

[KootK]

 

[RFreund]

Nice work with the Fruit.

I have reached a definitive answer on this. The unbraced length is the entire beam length even using the AS4100.
I went back and looked in the 6th Edition to the Stability Design Criteria for Metal Structures. The formula used in AS4100 for M_o is the closed formed solution for the critical buckling moment for beams subject to a uniform moment. They specifically discuss our example case and specify the use of entire bottom flange if any portion of the bottom flange is in compression. They also give a special "C.b" or "alpha_m" factor that can be used which recognizes the benefit of the lateral restraint of the top flange. Below are some snippets.

Here is the closed form (same as AS4100):

Braced Points Are Not Inflection (I know this was already posted, but this is part of the same document that derives the LTB equation)

Influence of Cont Bracing on One Flange

Modified Cb

Where do we go from here?
1.) Speculate why AS4100 seems to indicate you can use a shorter segment? Kootk I think has this covered with his theory. I think he's been miles ahead of me on this the entire time.
Or figure out if the code is really telling you to take the entire length.

2.) Try to back calculate C.b using Mastan2. If I use the modified C.b factor I get 3.667. That means that the nominal capacity would be 393 kip*ft or 532.2 kNm. This is higher than the elastic buckling we found with mastan2. So let's scrutinize both.

EIT

http://www.HowToEngineer.com

 

[RFreund]

So I'd like to get agreement on the hand equation results with the Mastan2 results (without having to contact Dr. Z).

Questions in mastan:
Kootk - How'd you know to add nodes and apply to the load to the top of the "fake beam" and also apply restraints to the top of the "fake beam"? Just using line elements and placing everything at the centroid seems wrong, but I didn't even realize that you could take in account load height an restraint location in Mastan2. Did you see an example of this somewhere? I'm just trying to understand the program better.

Problems with Cb:
The modified equation seems to be specific to a uniform load not a point load. Maybe this is giving the error. Maybe we try to model a uniform load in Mastan2?

Hand equation: 107 kip*ft x 3.667 = 392.6 kip*ft
Mastan2: 285 kip*ft

EIT

http://www.HowToEngineer.com

 

[KootK]

Alright, consider me your Mastan support staff if you need that. Or are you planning to do the Mastan yourself?

Kootk - How'd you know to add nodes and apply to the load to the top of the "fake beam" and also apply restraints to the top of the "fake beam"? Just using line elements and placing everything at the centroid seems wrong, but I didn't even realize that you could take in account load height an restraint location in Mastan2

I took an experimental, evening graduate class in nonlinear structural analysis at Marquette back in 2005 with a professor who runs in the same circles as Dr. White and Dr. Ziemian. The course was awesome but would have been more aptly titled "Nifty Stuff from Dr.Z's Textook". We did a lot of Matlab etc but also spent a lot time with Mastan and worked through a lot of the precursors to what eventually became the Stability Fun series. Of course, that was fifteen years ago now and my long term memory is crap for anything other than first principles stuff.

Using line elements placed at the centroids is just what you do, for better or worse. Some notes on the fake beams in my models:

1) All of the fake beam line elements were the same cross section as the beam itself. This was really just a matter of convenience. Mastan is not super user friendly and it's a boon just to be able to click "All Members" and apply the same cross section to everything.

2) All connections between all member segments, including the fake beam elements, were rigidly connected for both flexure and warping torsion. Again with the "All Members" business.

3) For the most part, the fake beam elements are nothing more than visual aids to allow the user to visually perceive the rotation of the beam in addition to the centroidal displacement. The one important job that they do, as you surmised, is allow you to introduce loads and restraints at locations in space other than the beam centroid.

4) If you look closely as some of the Mastan output, you'll see that the presence of the fake beam elements does actually impact the results a bit. Those impacts are very small however and, for most intents and purposes, the fake beam elements can be considered purely "ride along", as we intend. For some of the models that I ran where the applied load ratio was in excess of 1.0, the first mode of buckling was actually the center tee stub of the fake beam twisting around ninety degrees like a goofy corkscrew. So there's that. I just put a fake x-dir restraint on the fake top flange and forced the real first mode to bubble back up to its rightful place at the surface.

5) I entertained the notion of trying to strategically chose the cross sections for the fake beams. One the one hand, you want something relatively flexible and inconsequential to minimize the impact on the overall beam behavior. On the other hand, you kind of want something stiff so that the applied loads move around with the beam rotation as you'd expect them to without any bonus flexibilities coming into play. In the end I concluded that, either way, the impact was going to be so negligible that it wasn't worth extra effort of trying to get fancy(er).

The modified equation seems to be specific to a uniform load not a point load. Maybe this is giving the error. Maybe we try to model a uniform load in Mastan2?

Sure. Do you want me to do this? Would you mind if we dropped the 70' beam example and migrated to back to the 32' test case? With the 70' case, I fear that our results will forever be tainted by "sure, but at 70' it's not a realistic example and, therefore, not wholly valid for comparison with code provisions". I actually feel that waay myself. The 70' example did it's job admirably as the hyperbolic example that it was intended to be but I think that it's time to put that one out to pasture in favor of something more representative of practical designs. Even at 32', Mastan's coming in at only 50% of the AS4100 capacity so there's still plenty of discrepancy to fret over.

How about this:

- W27x84
- 1/8 th point top flange lateral bracing.
- Uniform load producing a peak moment near the plastic moment as before.
- 32' span
- Fixed beam ends.
- Weak axis rotation unrestrained at beam ends.

If you agree to this, I'll run it as listed above and modified as follows for Cb calculation:

- Remove all intermediate restraints.
- Move all load down to the shear center.

 

[KutEng]

As a kid when I dreamt of becoming an engineer I never once thought I'd be sitting here looking at an analysis of fruit content titled "Cornucopia of beam failure modes"...

I'll never be able to look at an apple the same that's for sure

 

[Tomfh]

Even at 32', Mastan's coming in at only 50% of the AS4100 capacity

Can you please lock the bottom flange at the L restraints (ie turn the L's into F's) and see what it does to that 50%?

Regarding span lengths, I think 32' is too short for a W27 if we're talking about AS4100 steel rafters and want to have a "realistic" arrangement.

 

[KootK]

Sure. What do you like at 32'? 18x35? 16x26? I'd always intended for a low Iy/Ix to promote LTB. Where an L-brace is at the tension flange, you want it gone completely, right?

 

[Tomfh]

Sure. What do you like at 32'? 18x35? 16x26? I'd always intended for a low Iy/Ix to promote LTB

I was thinking more like Span to depth of 40+

Where an L-brace is at the tension flange, you want it gone completely, right?

No, I meant bracing all of the restraint points top and bottom, to make them all F restraints. To see how L restraints along the top compares to F restraints along the whole beam.

AS4100 is assuming L restraints are equivalent to F restraints. I'm curious as to what mastan says is the difference between the L restrained vs F restrained beam.

 

[KootK]

W10x12 coming up then, all braced up. I"ll put my money on it going past plastic section capacity.

 

[Tomfh]

Can you compare to the L case too, for that particular beam...

 

[KootK]

W10x12
Mid-span point load = 12 kip (full section yield at 11.7k)
Span = 36'
File: Link

Run #1: ALR = 0.19055; L-braces everywhere.

Run #2: ALR = 0.68169; F-braces only at locations consistent with AS4100.

Run #3: ALR = 3.2025;F -braces everywhere.

 

[Tomfh]

What’s the unrestrained capacity of that beam?

 

[KootK]

Not much it seems. ALR = 0.069133. Unadjusted, elastic LTB "capaccity" as usual.

 

[Settingsun]

Why does the cross section stretch in those images?

 

[KootK]

As I described in my response to RFreund, the cross sections represent nothing at all in terms of reality. Just visual aids and a way to apply restraints and loads to locations other than the beam centroid. That said, they do draw a little load and, therefore, do deform a bit. For some of these buckling modes the deformation is incredibly small. So small that they are on par with the tiny cross section deformations which is why you see the stretching that you commented on. The reality is that these cross sectional deformations are present in all of the Mastan runs, they're just imperceptible relative to the other, much larger deformations in many cases. For comparison, in that last diagram in the bunch of three above, you're looking at a flange tip elongation measured in 10^-13 inches.

This is my best guess at least. It's difficult to parse out some of these effects.

 

[Tomfh]

I can only see two possibilities, unfortunately.

1. These buckling results are all wrong.

2. AS4100 simplified segment method can be unconservative when L restraints are used.


We could be missing something, but no ones coming up with much....

 

[KootK]

I messed up in a couple of spots when trying to explain the cross section distortions.

1) I shouldn't have given the impression that the nodal deformations were in inches. As mode shapes, they are entirely non-dimensional. When you look through the nodal displacements, you find that one of the nodes has a displacement of [1.0] and the rest of the nodes have absolute values less than [1.0]. And this is exactly as it should be given that the deflected shape is a normalized mode shape, not a real representation of displacement. A different kind of analysis, such as second order non-linear, would be required to estimate true displacements. For these Eigenvalue runs, the displacements are all just relative.

2) While it is true that the faux beam sections do draw some load and deform a bit, I believe that it was an error to suggest that those deformations were predominantly responsible for the sectional distortion that steveh49 commented on. Rather, I think that it works like this:

a) for some high energy mode shapes, the modal displacements of the buckled shapes are so small that they are of the same order as the displacements at the nodes of the faux cross sections.

b) All of the displacements get scaled twice: once for normalizing the mode shape and a second time to amplify the view for the operator. And this scaling applies to the distances between all nodes that have moved, including the nodes of the faux cross section.

c) Given [b & a], even a rigid body motion of the faux cross section may result in stretching of the distance between points, even when little to no stretching between points would be expected in the real, physical thing.

Applying this to the displaced shaped below, I would say that the points representing the top and bottom flange both moved in space, in opposing directions, as a result of mostly rigid body rotation. Then, when all of the distances between all of the displaced points were scaled, the proportions of the faux cross section got scaled too. This really is tough to explain but I'm fairly certain that we could tell a fairly similar -- and logical -- story about any of the other sectional distortions.