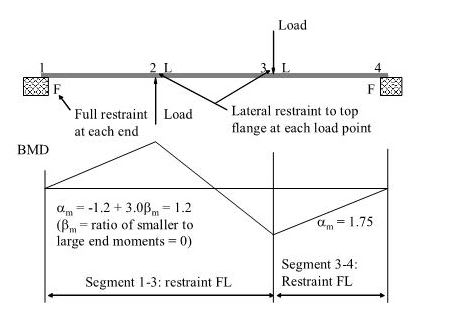
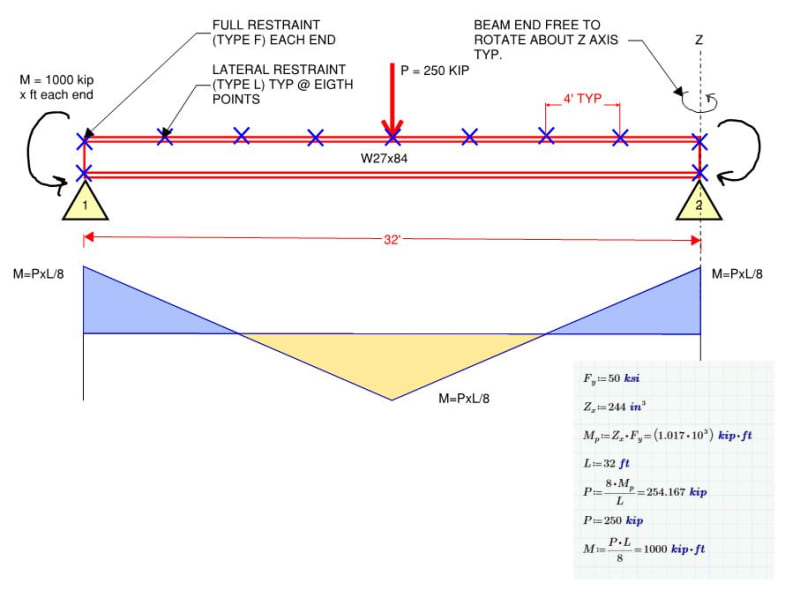
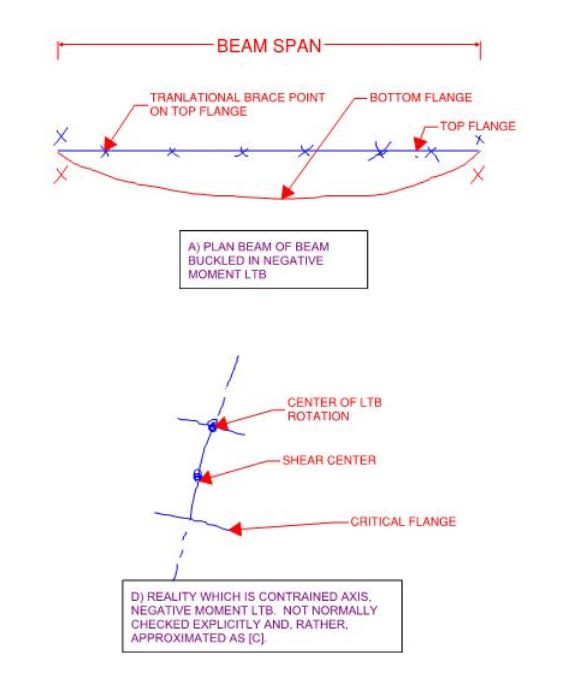
Human909 said:
Just an FYI. I looked at multimodes and still didn't see the buckling mode you described.
I'm not surprised. As I mentioned somewhere above, I think that it would take a pretty contrived example to make OP's real world situation go south. But I'm going to do my darnedest to contrive just such an example. We. Shall. See.
There's something about my world view here on Eng-Tips that I've been hesitant to share because it's difficult to articulate without my sounding like a raging egomaniac. I have something important in common with Albert Einstein. I know, right? Sadly, that thing is neither intelligence nor creativity. Rather, what we have in common is that we both consider the mental experiment to be the source of all understanding.
Almost everything that Einstein came up with was the byproduct of a a handful of mental experiments that required no laboratory work to develop. Yes, experiments were later done by others for verification and that was in important step. But Einstein didn't let the eventual need for such verification hold him back from dreaming the big dreams.
When I come at something hard here on Eng-Tips, I go straight for the root, physical theory of it and pursue that like a dog with a bone in a way that, frankly, some find off putting. I run my own mental experiments until I feel that I've gotten the model perfected in my head. For me, this is the way that I learn and discover. The flip side of this coin is that:
1) While I respect that FEM results have value, that's never sufficient for me.
2) While I respect that code interpretations have value, that's never sufficient for me.
3) While I respect that empirical testing has value, that's never sufficient for me.
4) While I respect that gobs of analytical data have value, that's never sufficient for me.
5) I tend scoff at homework assignments asking me to provide code interpretations, empirical data, analytical date, or FEM results. I just don't care all that much about these things compared to the root, physical model in my head.
So I guess that's my roundabout way of saying that I'm not overly concerned about whether or not your FEM model predicts the buckling mode that I described. If it can be predicted on paper, and in the model in my head,
that's what interests me. I would actually argue thatt he buckling mode that I described is the
only logical "next in line" mode regardless of whether it's "far off" or not. And I've got a hunch that this far-off-ness might be used to resolve the apparent discrepancy between "compression flange" and "flange that moves most". More on that later.
KootK said:
Oh and Kootk. Good to have you back, I hope the inlaws was fun!
Thanks, it's good to be back. I actually had to put this down not because of time constraints (doesn't take much) but because I was getting too distracted thinking about this to be "present" with my family. Found myself zoning out on conversations with people that I haven't seen in three years. Not good.