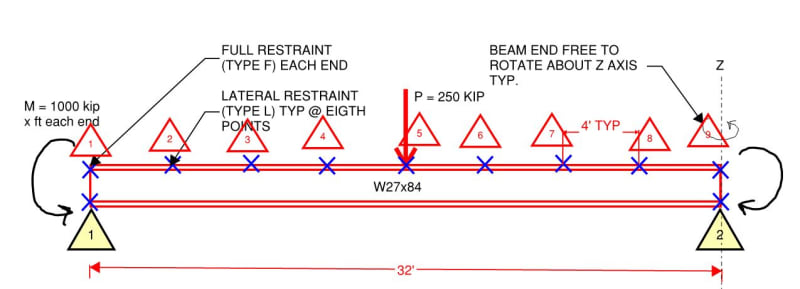
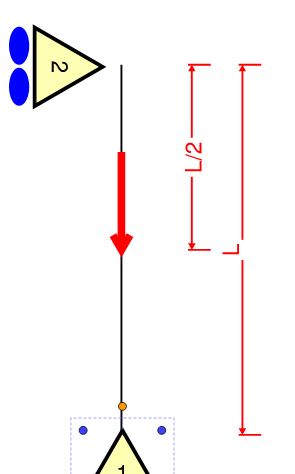
Hey. KootK. I feel like I might be making a high school level mistake here but I'm getting your beam well into yielding without even considering buckling. My input. 9.75m long, 1112kN load, 1355kNm moment on end. Result ~387mPa peak stress...
KootK said:
I'd also like for all parties to agree on the interpretation of the clause below.
I think we all disagree with this clause as far as applying AS4100 is concerned. It isn't in line with how it is use or the spirit 5.5.2 and 5.5.3. That said logically your clause could be superior but it is impractical and is also potentially self referential. ie restrain 1 depends on restraint 2 and restraint 2 thus depends on restrain 1.
Here is the output:
AS4100 1998 CALCULATIONS FOR GROUP 1 (*=Failure)
------------------------------------
Critical load case is 1, out of 1
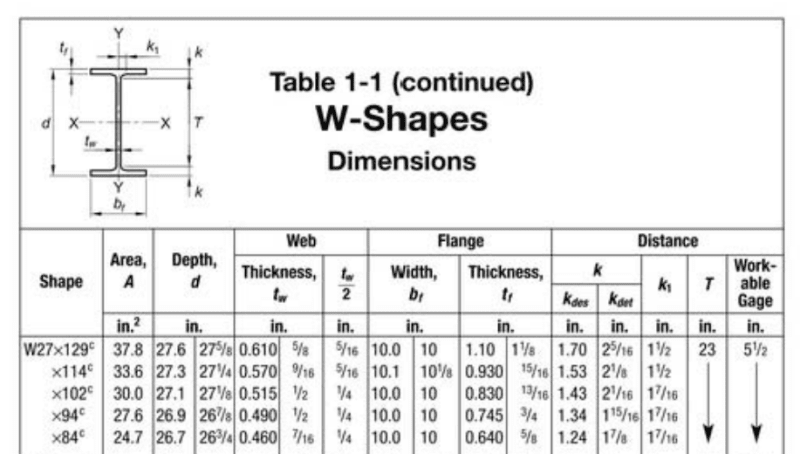
Section: *W27x84 (I or H section, Rolled/SR)
Failure Crit Start Finish Axial Major Minor Major Minor Load
Mode Case Pos'n Pos'n Force Shear Shear Moment Moment Factor
Section 1 0.000 0.00 0.00 556.03 -1355.82 0.00 0.66*
Member 1 0.000 2.438 0.00 -1355.82 0.00 0.66*
Shear 1 0.000 0.00 0.00 556.03 -1355.82 0.00 0.74*
(1.00)
Grade= 36 Fy = 248.2 MPa
Fyw = 248.2 MPa Fu = 399.9 MPa
Ltot = 9.754 m Lseg = 2.438 m (FL Bot-Top)
kt = 1.00 (5.6.3) kl = 1.00 (5.6.3)
kr = 1.00 (5.6.3)
Le = 2.438 m (Bending) (5.6.3)
Lx = 9.754 m (Compression) Ly = 9.754 m (Compression)
Lz = 9.754 m (Torsion)
Ly/ry= 185.4 (Compression) Le/ry= 46.3 (Bending)
Arf = 0.0 mm^2 Arw = 0.0 mm^2
An = 15935.5 mm^2 Ae = 0.0 mm^2 (6.2.2)
Kf = 0.00 (6.2.2) Kt = 1.00 (7.3)
αm = 1.82 (5.6.1.1) αs = 0.93 (5.6.1.1)
αcx = 0.00 (6.3.3) αcy = 0.00 (6.3.3)
αb = 0.00 (6.3.3) βme = 0.00 (8.4.4.1)
βmx = 0.50 (8.4.2.2) βmy = 0.00 (8.4.2.2)
γ = 0.00 (8.3.4) ϕ = 0.90 (3.4)
N* = 0.00 kN
Vx* = 0.00 kN (not considered) Vy* = 556.03 kN
Mx* = -1355.82 kNm (Compact) My* = 0.00 kNm (Compact)
ϕNt = 0.00 kN (7.2) ϕNs = 0.00 kN (6.2)
ϕNcx = 0.00 kN (6.3.3) ϕNcy = 0.00 kN (6.3.3)
ϕNoz = 0.00 kN (8.4.4.1) ϕMo = 4476.96 kNm (5.6.1)
ϕVvm = 631.26 kN (5.12) ϕMf = 610.55 kNm (5.12.2)
ϕMsx = 893.21 kNm (5.2) ϕMsy = 116.41 kNm (5.2)
ϕMbx = 893.21 kNm (5.6) ϕMox = 0.00 kNm (8.4.4)
ϕMrx = 0.00 kNm (8.3.2) ϕMry = 0.00 kNm (8.3.3)
ϕMix = 0.00 kNm (8.4.2.2) ϕMiy = 0.00 kNm (8.4.2.2)
ϕMtx = 0.00 kNm (8.4.5.2) ϕMcx = 0.00 kNm (8.4.5.1)
Mx*
---- = 1.52 > 1.00* (Fail) Flexural-torsional buckling (5.6)
ϕMbx