Rafter without fly brace? 22

[fourpm]

I am designing rafters to AS4100 and wondering what if I don't use fly brace. I understand that with fly brace it will give you full restraint. But if I don't use fly brace, will the purlin above be considered as lateral restraint for rafter under uplift? If so. can I take the purlin spacing as segment and the only factor that changes without fly brace is kt?
I have the same question when it comes the continuous steel floor beam design where Z/C floor joints sit on top of the beam. What segment should I take for the beam near the support? Can I take the floor joists spacing as segment with lateral restraint? Can anyone give me some examples? I have read some manuals but the examples they have are simply supported beams only. Thank you.

 

[Tomfh]

1) I have an older version of AS4100 and have read that.

2) I have some steel texts based on newer version of AS4100 and have read those.

3) I asked you and Agent666 to share the recent versions of the AS4100 so that I could participate more meaningfully in this discussion. So, if I'm missing information, that's on you.

4) If your version of AS4100 has some magic bullet clause that I haven't seen yet, and would refute my arguments, produce it. Something tells me that you already would have if it existed.

The relevant clauses, definitions, and underlying principles have been around since the first edition of AS4100, and indeed well before that, so your "old" copy should allow you to contribute.

5) I think that it's poor form to deny my right to participate in this discussion just because:

No-one's denying your right to contribute. I'm merely asking that you familiarise yourself with AS4100 before telling us all what's wrong with it, and before telling us what's wrong with how it's taught, understood, and practised.

AS4100 does not view segments (and sub segments) the way you do. It is not wedded to Yura's (very general) advice to only count points of full twist restraint.

If you feel AS4100 is "flawed", then show how it is. You would need to show that AS4100 as written overestimates buckling capacity. If you can do that it would be a very important contribution.

You're unable to settle this debate as you'd like by way of logical argument.

The argument is that lateral restraints, whilst inferior to full restraints, do nonetheless enhance lateral torsional buckling capacity and that therefore AS4100 is justified in allowing designers to consider them.

 

[Agent666]

This post will concentrate on stating exactly how the code requirements are intended to be interpreted. They might not reflect other realities, but they are a set of rules that is intended to result in a lower bound capacity being determined.

Firstly I wanted to say, there are some people who are fundamentally misinterpreting the AS4100/NZS3404 provisions in this thread and twisting the words to their own related but incorrect interpretations. I suspect this reply will maybe be meet with further disagreement and requiring endless proofs, which is fine.

I feel sometimes threads on lateral stability sometimes devolve into an argument a little like trying to convince a flat-earther that the world is round or vice versa, despite the common knowledge and education systems and so forth (including real proof) having known for a few centuries that the world is in fact round. No matter of proofs will convince the other side of the argument, this is a fact. I don't mean this to be derogatory at all to those on the alternative side of the debate, but sometimes everyone is wrong about something and this is one of those times I feel with people who have never used the AS/NZS standards trying to say we're applying the provisions which we have grown up with all wrong.

First a bit of background, I was taught steel design by John Butterworth, who was on the original NZS3404 1997 standards committee, he died a few years ago so I cannot ask him for clarification/proof/confirmation or other such things that people contributing to the thread are asking for. More recently I've also worked with a lot of people who have been taught steel design by Charles Clifton who was also on the 1997 standards committee when he was working for HERA. He currently teaches at the University of Auckland.

Now I like to think those guys therefore know what they are on about, and teach the standard in the intent it was meant to be interpreted without any twisting of words being required. After all they wrote and contributed to the standard as it is today. Now while those names might not mean anything to anyone outside of New Zealand, they were and are quite well respected in NZ, having taught generations of Engineers.

No doubt as other Aussies/NZ'ers who have contributed can attest to having been taught, and interpreted the provisions of the standard in the same manner I'm outlining below by other eminent people from this part of the world in the steel/stability world like Nicholas Trahair or Mark Bradford, etc, etc.

TLDR - Believe people who study and work in NZ and AU would know how to correctly apply their own code provisions.

Firstly some background/clarification on definitions so we are talking AS/NZS nomenclature (note all taken from NZS3404, but I'm sure they are similarly defined in AS4100).

Firstly let's look at a support, basically boils down to F or P restraint.

Definition of a member, basically boils down to a segment or number of segments:-

Role and definition of a segment (please note the use of 'cross section' here, more on this later when we get to the critical flange definition):-

Definition of a cross section:-
Well one isn't included, but it's fairly obvious based on the segment definition and the language in the entire remainder of the standard that 'cross section' is actually simply a point along the member where you may apply a restraint or evaluate the member or section capacity.

Definition of critical flange

THE IMPORTANT BITS OF INTERPRETATION ON THE ROAD TO CRITICAL FLANGE DEFINITION IN ACCORDANCE WITH AS4100/NZS3404:-

1 - A member is the physical member between supports with F or P restraints, or basically also saying you need F or P restraint at supports

2 - A member can be made up of a number of segments with F, R, L or U restraints at segment ends

3 - The member capacity is determined on a segment by segment basis

4 - Cross section means a point/location at the ends of a segment where a restraint is applied

5 - Critical flange is defined as the flange at any cross section (i.e. at the exact location of the restraint) which in the absence of a restraint at that cross section would deflect the furthest, which one deflects the furthest is determined usually by applying either the requirements of 5.5.2 or 5.5.3. Basically 5.5.2 says at that particular location of the restraint, if the top flange is in compression (for a segment with restraint at both ends) then the critical flange is the top flange. What goes on beyond the location of the restraint is irrelevant for assessing this (I feel this is the point people are missing for applying these provisions).

This is how the requirements are applied and intended to be applied and how they are taught by the people who wrote the standard, etc, etc. You can have an alternative view, but in this particular case you would not be correct.

I'm guilty of not using the correct terminology, the reference to the cross section in the definition means just that. Consider a small slice of the members length as the cross section. So the definition of the critical flange is not based on looking at a member or segment and seeing if it were to buckle as an entire member or segment to see which flange goes furthest. I'm guilty of saying this I think earlier on in the thread (I didn't read back through the first bit as its pretty heavy going!).

For application of the requirement for defining the critical flange all you are doing is looking at the location of the restraint in isolation and classifying the cross section based on the clause 5.5 criteria based on which flange is the compression flange typically as noted in 5.5.2 (though can be both the tension and compression flange for a restraint on a cantilevered end as noted in 5.5.3).

This is the way it is taught, interpreted, used, a theme noted by several posters here. There is no magic about it or mystery. I think in my brain when I read the criteria for critical flange I convert cross section to mean segment as some others have in an effort to understand how to apply the provisions. But this isn't the case if you fully want to apply it as intended. It says cross section for a specific reason.

I certainly always apply it based on the actual cross section and forces present only at the location of the restraint, as does everyone else who I've ever run into who actually practices in AS/NZS. I'm sure the other posters will back me up if I say this is it, anything else is incorrect. Tomfh and others have tried to explain how to interpret, or at least say other interpretations are not correct.

The rest of the length of the segment could be in a big black box for all I care for applying these provisions, you don't need to know what is going on along the segment. It is 100% irrelevant for application of the restraint/critical flange requirements. You only need to know the compression flange at the point of restraint.

What goes on along the member is allowed for elsewhere as is member imperfections/residual stresses/moment distribution in the form of the alpha_m and alpha_s factors.

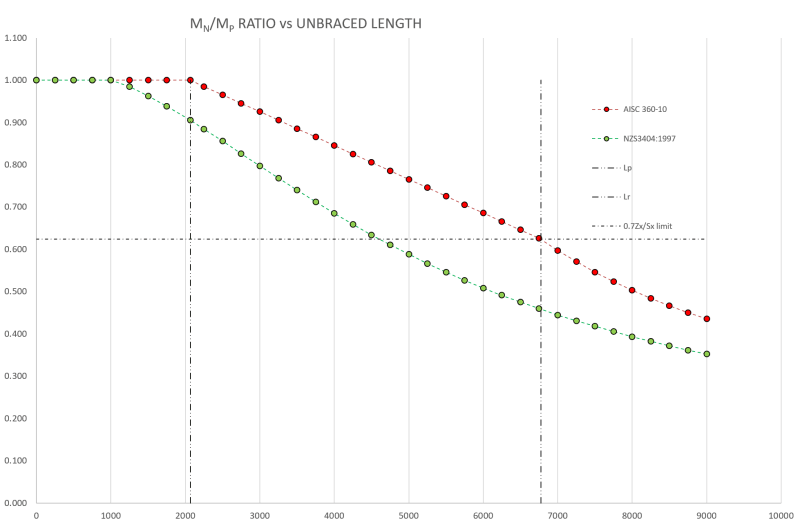
I would point out when making comparison regarding different codes and people saying we're all doing it wrong down in this part of the world. The AS4100/NZS3404 curves are far more conservative than AISC curves for lateral torsional buckling, or alternatively the AISC curves are far less conservative than the AS/NZS capacities. So maybe you nothern types are doing it wrong, a debate for another day perhaps..... All I know is if designed correctly following your code of choice, shit shouldn't fall down.

My understanding is that this is because the AS/NZS curves are scaled to all be lower than experimental results (the 0.6 factor in the alpha_s calculation is responsible for this). As opposed to AISC which takes more or less an average path through all the experimental data, accepting that some real members could in fact have a lower capacity than predicted by the code. For example, here's something I prepared earlier comparing the capacity between AS\NZS and AISC codes for the same member/situation:-

You would need to show that AS4100 as written overestimates buckling capacity. If you can do that it would be a very important contribution.

 

[Tomfh]

Agent,

Good post.

Yes Australian practice is to assess the cross section at the location of the lateral restraint. The flange can be considered laterally restrained if it would buckle farthest in the absence of that restraint, or if that flange is the compression flange. These L restraints define your segments (“sub segments” in AS4100 terminology), which defines your effective length. So we appear to be in full agreement here.

The part I find murky is the critical flange definitions. Sometimes the flange which will buckle farthest is not the compression flange.

I’m not sure if this is deliberate and the code is saying that it’s fine to take either flange as critical on these situations, or if something else is going on. It would be interesting to see some buckling charts comparing the effectiveness of

1. Restraining the flange which will deflect farthest

And,

2. Restraining the compression flange.

Maybe both are perfectly adequate. I’ve run a few buckling analyses and it seems like much of the time it really doesn’t matter where you brace the cross section as far as preventing lateral torsional buckling.

So maybe the critical flange logic isn’t so much about identifying which of the two flanges will prevent buckling, and which one won’t, but is about weeding out especially crappy points of restraint.

 

[Agent666]

All the code is saying is restrain the compression flange at the point of the restraint, because it defines this as the critical flange being the one that would deflects the furthest at that point. It defines this 'deflecting the furthest' thing as being satisfied if you basically restrai whichever flange is the compression flange for a segment with restraint at both ends, or both flanges for free at one end.

It's not expecting you to do some fancy analysis to prove it which I think others are getting bogged down on, its just a criteria that you apply directly. Whether the flange at that location really does deflect the furthest in reality is irrelevant, as you say even a 'L' restraint to the non-critical flange actually does something if you go through the buckling analysis route (i'd ignore it though, but just saying), even if it's not relied on in terms of the code.

Providing the right type of restraint to the non-critical flange like twist restraint still results in a P restraint at that cross section. Which for all intents and purposes is no different to direct restraint of the critical flange. Providing restraint to the flange in compression irrespective of where the restraint is improves the effective length.

I would point out under reversing moment, at one end of the segment you'll have the top flange critical, at the other the bottom. Again, nothing to do with what might be going on in between as far as the interpretation goes for which flange you are considering as being critical and requiring/having restraint.

The part I find murky is the critical flange definitions. Sometimes the flange which will buckle farthest is not the compression flange.

In NZS3404 this is much clearer in our NZ code. Where it states for a cantilever both flanges are critical. I believe AS4100 says only the tension flange is critical. Any other situations you were thinking of particularly? AS4100 doesn't clarify this aspect at all.

There are a few subtle differences in NZS3404 that are not contained in AS4100, for example some of our local plate slenderness limits are subtly different, our angle member design provisions are quite different, and we don't for some reason have the block shear provisions that are in AS4100. Plus obviously we have all the multitude of seismic provisions, including quite a few other limitations on sections and some unique combined actions checks that are not present in AS4100.

 

[Tomfh]

All the code is saying is restrain the compression flange at the point of the restraint, because it defines this as the critical flange being the one that would deflects the furthest at that point

Yes I understand. But in reality the compression flange is often not the flange which will deflect the furthest. Eg in our original example here it is the bottom flange which will buckle the farthest in the absence of restraints. Thus at midspan you could take the bottom flange as critical, given that it will deflect farthest in the absence of restraint, OR you could take the top flange as critical, given it is the compression flange.

It is interesting that in Nz3404 both flanges are critical for a cantilever. Are they saying you must restrain both? Or are they saying you may take your pick which one to restrain?

 

[Agent666]

That's the thing, maybe not out in the span, but at that particular point of the restraint if you considered that little slice of the beam then I think it's interpreted as the compression flange is more likely going to deflect further than the tension flange at that particular point forgetting about anything else going on beyond that point. This is how you need to apply the provision, it's how you were taught to do it whether it was explicitly explained or not.

You're still thinking about buckling in the span though with your explaination/thinking in the last post. That's not how you interpret the code requirement. You need to stop thinking like that. Whats going on in the span has nothing to do with applying the provisions. It's all about the cross section at the point of the restraint.

 

[KootK]

Kootk, you really should read AS4100 before you explain it to everyone.

I think that it's poor form to deny my right to participate in this discussion just because...

No-one's denying your right to contribute. I'm merely asking that you familiarise yourself with AS4100 before telling us all what's wrong with it, and before telling us what's wrong with how it's taught, understood, and practised.

Ah...I see. When I initially read your comment, I mistakenly interpreted it as a petty attempt to diminish my contributions here because I'm non-Aussie. But now I realize that you really just wanted to help promote the success of my efforts by ensuring that I'm well prepared going forward. Thanks. It is, however, a bit presumptuous of you to assume that I'm not already familiar with AS4100. That, particularly, given that most of the relevant provisions are already posted within this thread and I've been commenting on them in detail for weeks now.

If you feel AS4100 is "flawed", then show how it is. You would need to show that AS4100 as written overestimates buckling capacity.

I would not need to do that and your thinking otherwise makes it evident that your missing the point of my arguments entirely. It's like is:

1) Theoretically, I believe that AS4100 is in complete agreement with the principles that I've been espousing. So there's no need for me to prove a numerical discrepancy because I've no cause whatsoever to believe that one exists.

2) I believe that you and Agent666 may be misinterpreting AS4100 and, as a result, overestimating LTB capacity. My concern is not that AS4100 is technically amiss, my concern is the you two are tehcnially amiss.

This will mix and match posts a bit awkwardly but, I think, is the ideal time to address this misconception:

...and people saying we're all doing it wrong down in this part of the world.

I have not said that ALL Australians are doing it wrong. I've only said that you and Tomfh are doing it wrong. There's an important difference there. Whether or not this as a systemic issue affecting many Aussies, I couldn't say (can't seem 'em from here). Rather, I'd be relying on you guys to tell me if this is a systemic issue.

3) The flaws that I feel I have identified in AS4100 are linguistic flaws, not technical ones. I feel that it is such linguistic flaws that have created the fertile ground into which all of these technical misconceptions have taken root. I sympathize with Aussie designers who struggle with interpreting these provisions because I know that I would struggle as well were our roles reversed.

 

[Tomfh]

It's all about the cross section at the point of the restraint.

I’m not following you. Maybe I’m misunderstanding it?

Your saying that even though the bottom tension flange buckles the furthest (in the absence of the restraint we are considering), that in terms of the cross section itself it’s the compression flange which buckles further?

 

[Tomfh]

I have not said that ALL Australians are doing it wrong. I've only said that you and Tomfh are doing it wrong

Agent is a kiwi. He is using NZ version, but the AU and NZ codes are quite similar.

In day to day practice we both design the same as most other aussies/kiwis - we take lateral restraints of the compression flange to be the defining points of effective length. This is what our codes say and what they intend to say.

 

[KootK]

Kootk, you really should read AS4100 before you explain it to everyone.

...people who have never used the AS/NZS standards trying to say we're applying the provisions which we have grown up with all wrong

...Believe people who study and work in NZ and AU would know how to correctly apply their own code provisions.

...as does everyone else who I've ever run into who actually practices in AS/NZS

Yeah, just look at all that hostility and resistance. And all, it seems, because you perceive me as an outsider because I don't own an Aussie passport. I get it though. It's not an easy thing to feel as though your long held, long cherished beliefs are being threatened by someone coming from the outside. In fact, I believe that it is one of the most difficult and impressive feats of a strong mind/ego to be able to allow itself to be changed in the face of new information that challenges old beliefs. I struggle with this constantly.

Consider however:

1) The AS4100 provisions that we've been debating are clearly causing confusion among designers and, therefore, could stand to be improved.

2) It's always difficult to assess things clearly when you're immersed in the dogma and group think of your own, day to day environment. In this sense, who better than an outsider to help sort things out?

In would encourage you both to take a glass half full approach to this and consider my involvement in this conversation a positive thing rather than a hostile threat from the outside. Tomfh suggested that I read up AS4100. I did that, in spades, weeks ago. And why would I do that? Because I'm genuinely interested in helping with this. It's tough for me to help, though, if you refuse to recognize the opportunity that my help represents.

 

[KootK]

Agent is a kiwi.

My bad, I knew that. You get the idea though. Antipodeans in general.

 

[KootK]

..need to point out that the following interpretation is actually incorrect.

Prove it. I believe that it is in fact your interpretation that is in error. And I've supplied a good deal of material above to substantiate that claim.

@Agent666: this post will be in response to the post of yours that began with this statement:

This post will concentrate on stating exactly how the code requirements are intended to be interpreted.

Some preliminaries:

1) Because of the sequence of how this has unfolded, I'm assuming that you meant for that to be the proof that I requested. That said, I found very little in your post resembling meaningful proof so it's difficult for me to tell. If I critique the proofiness of some sections of your post when, in fact, you never meant for those sections to be proof of anything, please forgive the error.

2) Your post was looong. And, as a frequent purveyor of long posts myself, I dig that. However, the length of your post made it a challenge for me to parse it an a manner that was a) efficient and b) short enough that other thread participants would actually bother to read it. To address this, I printed out your post and color coded it into sections that I felt represented different attempts at "proof". Going forward, I'll speak to each color coded section in turn. A copy of the PDF is attached.

3) The effort that you put into the response is apparent. And I'm grateful for that.

CRITIQUE OF THE PROOF

4) The RED section. This reads as "My professors, my colleagues, my dog, and my fish all do this my way. Therefore my way is probably the right way". This is a weak form of proof as opposed to, say, proof based on theory and physical reasoning. That said, I agree, it's a little something. There are some possible flaws to be considered however:

a) Mass delusions do in fact happen. The inflection point business of yore is a perfect example of this. It is in fact possible that all antipodeans believe as you do and are, none the less, wrong anyhow. Obviously, the odds of this are slim.

b) Far more likely, you may be misinterpreting the intent of your professors, your colleagues, your dog, and your fish in exactly the same way that you may have been misinterpreting AS4100. You are tainted, across the board, by your own preconceived notions. As are we all.

5) The YELLOW section. Frankly, I wasn't really sure what you were up to there. Yes, AS4100 and AISC are based on different curve fits. What does that tell us about how the AS4100 LTB provisions should be interpreted? Maybe you never intended to prove anything with this section and it's just an interesting factoid that you felt like sharing? Or maybe, like Tomfh, you mistakenly assumed that I challenge the validity of the AS4100 provisions on technical grounds. As I told Tom, that's not case. AS4100 and I are sympatico on the technical front. We only disagree with regard to what constitutes good technical writing.

6) The GREEN section. Here, it appears that you've simply restated your interpretations without offering up any particular proof in support of them. Moreover, you've presumptuously presented your interpretations as fact and mine as patently incorrect. Bold statements such as:

This post will concentrate on stating exactly how the code requirements are intended to be interpreted.

This is how the requirements are..intended to be applied...

You can have an alternative view, but in this particular case you would not be correct.

Ballsy stuff. It's like trying to debate with HAL9000. But, again, maybe you never intended for this section to prove anything. Maybe you just meant to demonstrate that you had a cohesive story to tell regarding the interpretation of AS4100. And a cohesive story is certainly better than a non-cohesive story.

 

[KootK]

So I got to thinkin'... if this wonky design method that Tomfh and Agent666 keep going an about is so ubiquitous, it must show up all over the place in Australian steel text books and design guides, right? And if that's the case, surely such documents would be worthwhile examples for us to ponder. So I set about trying to find such an example in my limited, antipodean library.

My quest was not an easy one. I have a text by the legend Trahair that, somehow, contained not a single example of an LTB check on a beam with an inflection point. But I hit pay dirt with a publication titled Steel Structures Design Manual to AS4100. In the preface, the authors describe the manual as "a self-instruction manual for beginners". Now we're speaking my language. I've attached an excerpt the relevant section of the manual to this post as a PDF.

So, when I read the example below, here's what I see:

1) And example from an authoritative, Australian source, dealing specifically with AS4100.

2) An example prepared by real antipodes rather than sketchy foreigners who don't know what they're talking about.

3) An example prosecuted according to the methods that I've espoused, verbatim.

4) An example prosecuted in a fundamentally different way to the methods espoused by Tomfh and Agent666

5) An example demonstrating that there's at least one Australian walking the face of the earth that sees things as I do.

 

[Tomfh]

Kootk.

That example contradicts everything you’ve been saying. It considers lateral restraints to be effective when they are attached to the compression flange. That is we’ve been saying from the start, and what you have been condemning.

 

[human909]

Edit: Thanks KootK for posting you example above. But I don't see how this contradicts Agent666's previous posts. His 'interpretation' does not seem to contradict mine. But to be honest I'm now all a little confused about where the disagreements between people here exist. (But maybe I just get confused easily.) Either way am reading all posts with interest.

Yes I understand. But in reality the compression flange is often not the flange which will deflect the furthest. Eg in our original example here it is the bottom flange which will buckle the farthest in the absence of restraints.

Sorry. Which example is this? In the rafter example the compression flange does defelect the most. In the continous beam example again the compression flange seems to defect the most.

Thus at midspan you could take the bottom flange as critical, given that it will deflect farthest in the absence of restraint

How do you figure this?

I believe that you and Agent666 may be misinterpreting AS4100 and, as a result, overestimating LTB capacity

Could you please give an example where the (mis)interpretation results in overestimating LTB capacity?

 

[Tomfh]

Sorry. Which example is this?

Continuous beam under gravity load. In the absence of the lateral restraints the bottom tension flange often buckles further than the top compression flange. Eg at midspan the bottom tension flange will often kick out the most during buckling, in the absence of intermediate lateral restraints, despite it being the tension flange at midspan.

Agent seems to be saying I’m doing it wrong to consider it that way, but I don’t really understand why. I thought that’s what the code meant by running a buckling analysis to see which flange buckles furthest in the unrestrained situation.

In any case I otherwise agree with Agent, and we approach it the same way in practice - by taking the compression flange to be critical. Eg the standard situation of counting purlins and joists as L restraints when they are attached to the compression flange.

 

[human909]

Continuous beam under gravity load. In the absence of the lateral restraints the bottom tension flange often buckles further than the top compression flange. Eg at midspan the bottom tension flange will often kick out the most during buckling, in the absence of intermediate lateral restraints, despite it being the tension flange at midspan.

Ok. I'm not seeing this in various buckling anaylisies that I'm looking at. But that isn't to say that the small range of scenarios I'm looking at are representative. Anyway debating this is probably distracting from the point. The simple rules regarding determinining critical flange can never be perfect. Hence the clause "The critical flange may be determined by an elastic buckling analysis.".

One would hope though that the simple rules regarding determinining critical flange remain conservative.

In any case I otherwise agree with Agent, and we approach it the same way in practice - by taking the compression flange to be critical. Eg the standard situation of counting purlins and joists as L restraints when they are attached to the compression flange.

I am wondering if everyone is in furious agreement here.

 

[jayrod12]

Eg at midspan the bottom tension flange will often kick out the most during buckling, in the absence of intermediate lateral restraints, despite it being the tension flange at midspan.

Do you have an example of this. I believe if you look at the mechanics of an unrestrained beam in positive bending it is the compression flange that buckles laterally, the tension flange is affected only by the buckling of the compression flange. Or are you meaning when the top flange is restrained but the bottom is not?

 

[Tomfh]

I am wondering if everyone is in furious agreement here.

No, because kootk has been arguing from the start that you cannot count L restraints to reduce your effective length.

 

[Tomfh]

Do you have an example of this. I believe if you look at the mechanics of an unrestrained beam in positive bending it is the compression flange that buckles laterally, the tension flange is affected only by the buckling of the compression flange. Or are you meaning when the top flange is restrained but the bottom is not?

I am not talking about when the top flange is restrained. I am taking about the case with no restraints, except the full restraints at the supports.

When a beam buckles it tends to do so globally, it doesn’t necessarily buckle in and out as flanges change from compression to tension. In these examples it’s often the bottom flange which buckles the most at every location (in the unrestrained case), even where the bottom flange is the tension flange.