Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in

FEMA's Outdated Flood Zone Maps 21

Oops409

Oops409

Mechanical
Apr 25, 2024
187
0
16
US
Only 3% of residents in Asheville, NC, for example, had flood insurance, according to an article I read. Looking at FEMA's Flood Maps, it is understandable why residents would not have flood insurance.

FEMA flood maps will need to be updated to reflect modern risks, and risks due to more and more urbanization and growth since maps were developed, along with whatever weather cycles we are now experiencing.

Screen_Shot_2024-10-04_at_2.44.28_PM_ufmkwl.png


Marion, NC below

Screen_Shot_2024-10-04_at_3.06.57_PM_mxaqdk.png


 
Replies continue below

Recommended for you

Sort by date Sort by votes
3DDave, 1503-44, IRStuff - very nice explanations of potential energy radiated by a surface area. I have learned from your explanations and dug deeper into various derivations of units that ordinarily I would not care about. Math is beautiful.
 
Upvote 0 Downvote
TugboatEng said:
As engineers, does anyone find it disappointing that NASA's scientists think kJ/cm² is a measurement of heat content?
Click to expand...

Are you so politically biased you've forgotten that a kJ is a kW*s? Did you miss where I said "add a one second time period, and you get J/m^2"?

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Upvote 0 Downvote
Dik, Quote Me "Joules lose their volume at a 2D surface. They cannot exist there.
I was trying to make a joke. Didn't work.

Work is also measured in Ft-Lbs, Lbf, or N x Distance moved, not perpendicular distance from a force, so not same as moment. Unfortunately the units alone don't mention what they are doing. Ft-Lbf of work convert to energy, but Ft-lbf of moment does not.

-------------
My heat energy theory is ...
heat (energy) never has a volume, or if it does, its like a photon has a volume, when it needs to. In a substance energy effects on the substance are to excite vibration of its molecules and resulting collisions. Otherwise its just "energy". Energy can also be radiation, so its a packet, or a wave.

As far as volume is concerned, it cannot really be contained in a volume. Its always moving, fast or very slowly. We cannot stop it, so it cannot be stored for long. It moves at its own free will from hot to cold. We can slow it down by butting things in its way. When it stops, it must become part of the entropy of that substance. When it moves, it must move as a point. It does not seem to have an associated volume bigger than a photon, so if it moves as a volume, it must be extremely thin in the direction of movement. If enough of it moves, I'd suppose that it is moving through an area and you have a flux of it. J/m2. Over time, you could measure W/m2 as it passes.

-------------




--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
Upvote 0 Downvote
Summer SCUBA Diving in Texas deep hill country lakes we would always find a thermocline at a 20' depth.
Above, water temp in summer could be in the 80's. (Air Temps 100+) Below it was in the upper 50's, Similar to the deep limestone caves in the area.




--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
Upvote 0 Downvote
Considering the time unit converts energy to power. Seconds are only needed when you want to know the power that has fallen on, or radiated from, or passed through a surface, or system envelop. Otherwise you just have an instaneous measure of energy.


--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
Upvote 0 Downvote
In case anyone missed it; the OHC maps are TWO DIMENSIONAL, so it makes sense that the metric is J/cm^2, since the 3rd dimension is compressed this map. I suppose, technically, they are 3 dimensional, with OHC being the 3rd dimension, as expressed in color.

For those whose physics senses aren't polluted by politics, this makes even more sense when you consider it would take TWO maps, one with mean OHC/depth and one with depth as 3rd dimensions; everything is nicely summarized into a single map.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
OHC(Ocean Heat Content). Screen shot from NOAA
IMG_7725_zypqum.png


Definitions
IMG_7724_akfsnt.jpg


Here is AI response to the question, What is heat content?
Per the Wikipedia article on enthalpy, the term "heat content" originating in the 19th century is a now an obsolete term, though still used. That's because, as you apparently already know, heat is energy transfer due solely to temperature difference. Heat is not something "stored" in a system. The proper term for that is internal energy.

So, could "Heat Content" Be a measure of how much heat is theoretically available to transfer between two bodies.
It is not "heat content" that is theoretically available to transfer between two bodies. It is internal energy that is theoretically available to transfer between two bodies, either by the mechanism of heat or work. From the first law for a closed (no mass transfer) system

ΔU=Q−W

If W=0 then the only mechanism to transfer energy is heat, Q. It is in this case, where heat is the only mechanism available to transfer energy, where one of the reasons the misnomer "heat content" arises.

Could it be the sum of all particles individual kinetic energies?
Again, substances do not contain heat. Substances contain internal energy, which is the sum of the kinetic and potential energy of all the particles of the substance at the microscopic level.
Click to expand...


Does anybody know how to edit the title of this thread, to say "FEMA- Federal Emergency Migration Assistance" where there are no limits!

🤓
 
Upvote 0 Downvote
Questioning data presentation is always reasonable - but with clear explanations of the OHC data presentations the sensibility of the units is without question.
 
Upvote 0 Downvote
Questioning data presentation is always reasonable - but with clear explanations of the OHC data presentations the sensibility of the units is without question.
Click to expand...

Which begs the question, does a molecule of water occupy a surface area or a volume?
 
Upvote 0 Downvote
Yes, it does.

When one this sentence into the German to translate wanted, would one the fact exploit, that the word order and the punctuation already with the German conventions agree.

-- Douglas Hofstadter, Jan 1982
 
Upvote 0 Downvote
[colorface][flip][bugeyed] SPOILER ALERT [bugeyed][flip][colorface]

I see what you did there!

If one wanted to translate this sentence into German, one would take advantage of the fact that the word order and punctuation already correspond to German conventions.
 
Upvote 0 Downvote

I guess I'll have to start taking your stuff as a joke.

-----*****-----
So strange to see the singularity approaching while the entire planet is rapidly turning into a hellscape. -John Coates

-Dik
 
Upvote 0 Downvote
No question that molecules have volume, thence also have a surface area.
We can quantify any attribute of the molecule in terms of m3, or m2, or lbm, or by any of its other attributes.
Consider its surface area.
If the molecule shape approaches that of a sphere, Area=4[π] r^2
If the molecule shape is a BCC crystal, Area=6*x^2, where x = width=height=length
We could now quantify heat based on the molecule's total surface area.
If I chose to quantify a possible energy flow with respect to a particular direction, from hot to cold, that might be across only one surface of the cube and Area would be =x^2.
If I wanted to find the heat transfer from a cubic swimming pool, extremely well insulated on sides and bottom, but open to atmosphere above, the only relevant surface area is the top surface of the cube, x^2 I would find the heat available for transfer through the top surface, possibly in terms of a unit area of that surface. J/m2

If I had a spherical pressure vessel, heat radiated in all directions, then the surface area of the sphere seems useful. Again, J/m2.

The point being that, while there may be a volume with a heat source and we can quantify total heat available using that volume, then calculate that to a heat per unit volume, J/m3, heat is never transferred across a volume. If we calculate any amount of heat being transferred from that volume, it always passes through some surface area of that volume, hence the units are always going to be J/m2

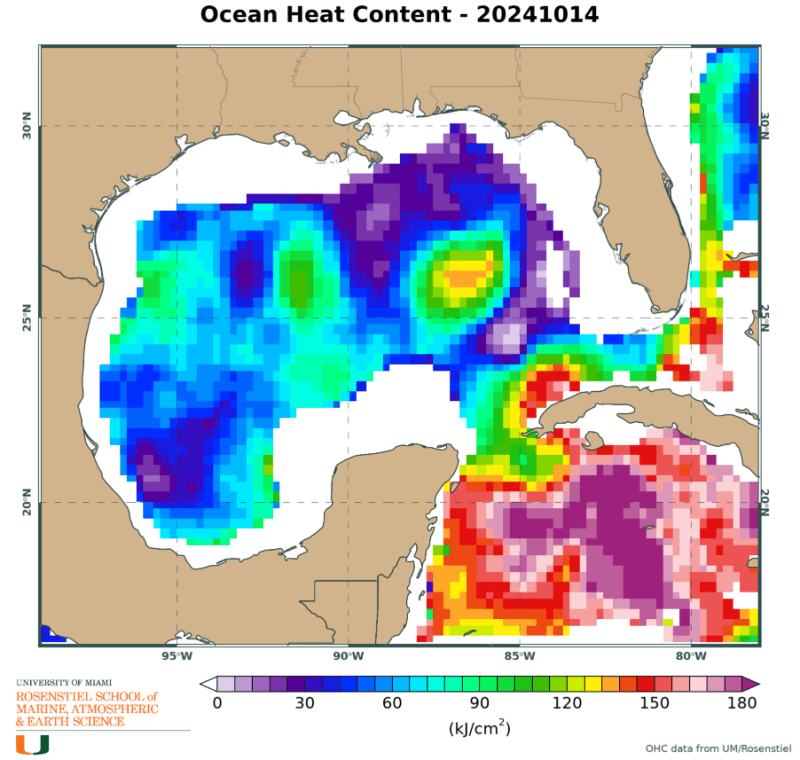
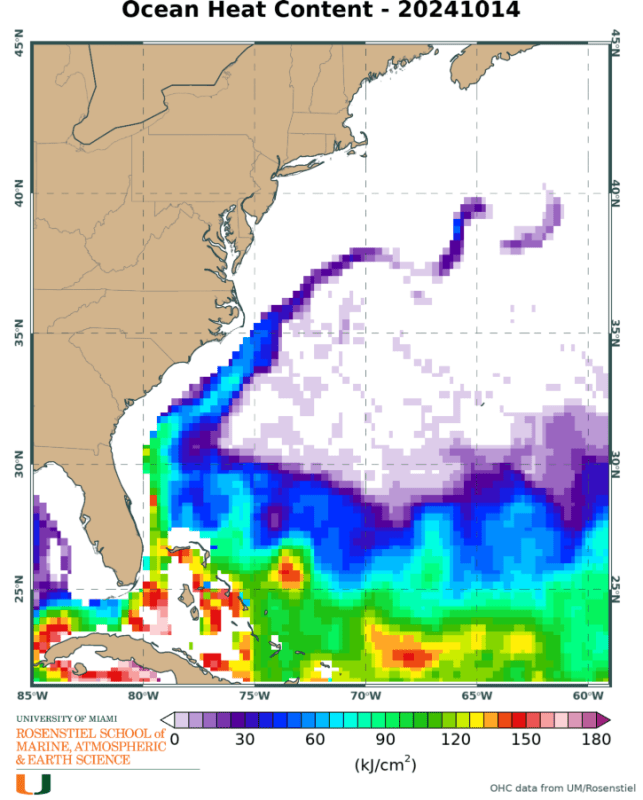
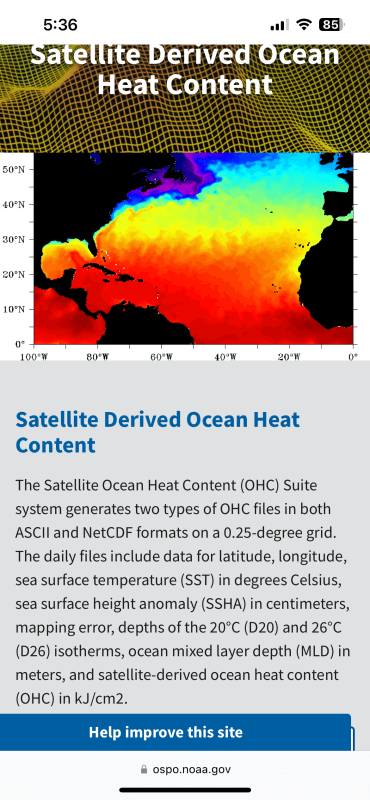
If units are J/m2, we are interested in what heat is available on a surface for transfer, in this case, at the ocean to atmosphere interface.






--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
Upvote 0 Downvote
You must log in or register to reply here.

Similar threads

Murph 9000
  • Locked
  • News
Residents evacuated in Nashville, Illinois after dam overtops and floods amid heavy rainfall
Replies
2
Views
6
FacEngrPE
FacEngrPE
Finch24
  • Locked
  • Question
Why heavy floods? 1
Replies
14
Views
15
FacEngrPE
FacEngrPE
JStructsteel
  • Locked
  • Question
New subway flooding in Brazil
Replies
13
Views
14
JStructsteel
JStructsteel
miningman
  • Locked
  • Question
Canadian Flooding
Replies
8
Views
20
itsmoked
itsmoked
msquared48
  • Locked
  • Question
Oroville Dam Spillway Concrete Failure (Feather River Flooding, CA) 36
22 23 24
Replies
477
Views
478
btrueblood
btrueblood
Back
Top